➤ Zeros da Função Quadrática
Já estudamos que o zero de uma função é um valor de \( x \) que anula a função, ou seja, o valor de \( x \) para o qual \( f(x) = 0 \).
Para determinar os zeros de uma função quadrática, devemos resolver a equação do tipo \( ax^2 + bx + c = 0 \), com \( a \neq 0 \).
Vamos explorar como resolver essas equações aplicando uma fórmula resolutiva, conhecida como fórmula de Bhaskara. Acompanhe a dedução:
| Procedimentos | Equações |
|---|---|
| Considerar a equação \( ax^2 + bx + c = 0 \) | $$ ax^2 + bx + c = 0 $$ |
| Multiplicar a equação por \( 4a \) | $$ 4a^2x^2 + 4abx + 4ac = 0 $$ |
| Adicionar \( b^2 \) aos dois membros | $$ 4a^2x^2 + 4abx + b^2 = b^2 – 4ac $$ |
| Identificar trinômio quadrado perfeito | $$ (2ax + b)^2 = b^2 – 4ac $$ |
| Extrair a raiz quadrada dos dois lados | $$ 2ax + b = \pm \sqrt{b^2 – 4ac} $$ |
| Isolar o \( x \) | $$ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} $$ |
Portanto, a fórmula resolutiva da equação \( ax^2 + bx + c = 0 \) é:
$$ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} $$
$$ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} $$
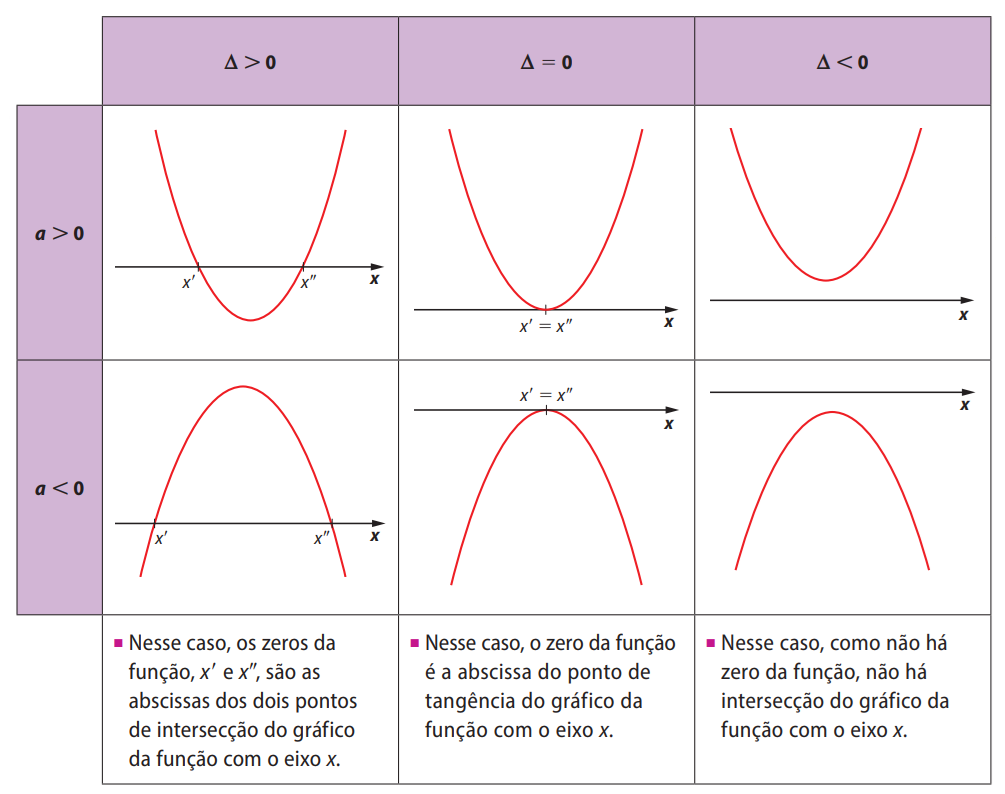
A expressão \( b^2 – 4ac \), chamada de delta (\( \Delta \)), nos indica a natureza das raízes da equação quadrática:
➤ Análise do Discriminante (Delta)
-
I. Se \( \Delta > 0 \): a equação possui duas raízes reais e distintas.
$$ x_1 = \frac{-b + \sqrt{\Delta}}{2a} \quad \text{e} \quad x_2 = \frac{-b – \sqrt{\Delta}}{2a} $$
-
II. Se \( \Delta = 0 \): a equação possui duas raízes reais iguais.
$$ x = \frac{-b}{2a} $$
- III. Se \( \Delta < 0 \): a equação não possui raízes reais.
✅ Lembre-se: o valor de \( \Delta = b^2 – 4ac \) define a quantidade e o tipo de raízes de uma função quadrática.