O conceito de limite é um dos pilares fundamentais do Cálculo Diferencial e Integral. Ele permite entender o comportamento de uma função nas proximidades de um ponto específico, mesmo que essa função não esteja definida nesse ponto. Por meio do estudo de limites, é possível compreender a continuidade, o crescimento ou decrescimento de funções, e estabelecer a base para o cálculo de derivadas.
Esta lista apresenta 10 exercícios progressivos sobre limites, explorando casos simples com substituição direta, situações que envolvem indeterminações do tipo 00\frac{0}{0}00, fatorações e racionalizações. Além disso, cada exercício conta com resolução passo a passo, proporcionando ao estudante uma visão clara das técnicas envolvidas na análise de limites.
Recomenda-se que você tente resolver os exercícios antes de consultar as soluções. Bons estudos!
Calcule os limites.
1)
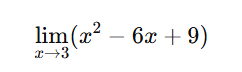
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
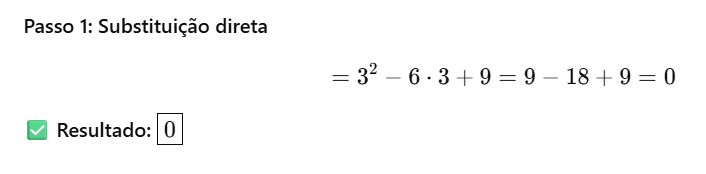
[/toggle]
2)
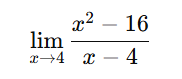
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
3)
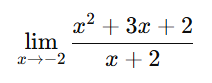
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
4)
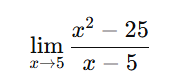
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
5)
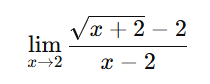
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
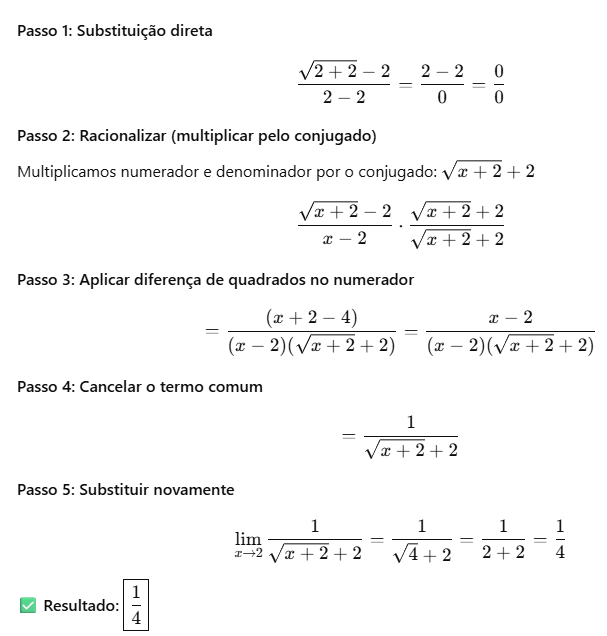
[/toggle]
6)
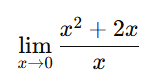
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
7)
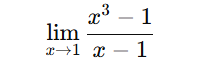
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
8)
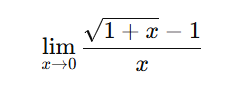
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
9)
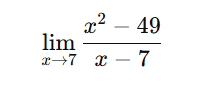
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
10)
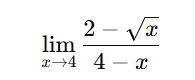
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

























