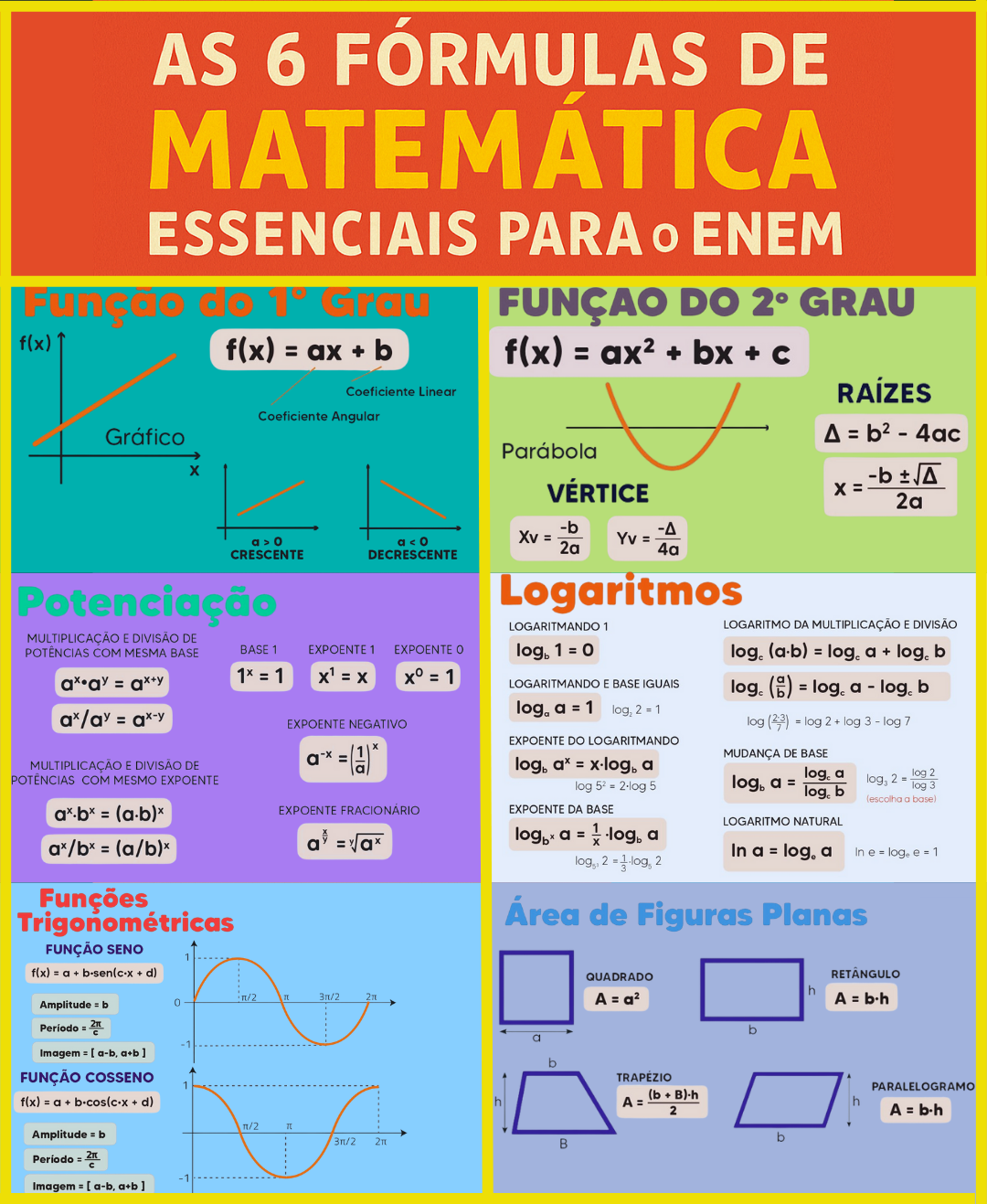
No ENEM, a maior parte das questões de Matemática se apoia em seis “famílias” de fórmulas. Dominar cada uma delas permite ler o enunciado, escolher o modelo correto e executar contas com segurança. Aqui você encontra um guia objetivo com função do 1º grau, função do 2º grau (vértice, raízes e Bhaskara), potenciação, logaritmos, trigonometria e áreas de figuras planas — sempre com um exemplo prático e uma pequena lista de exercícios com solução passo a passo.
Dica de prova: nas soluções, colocamos a matemática linha a linha (uma expressão por linha após o “=”) para evitar erros, especialmente em telas menores.
Baixe grátis: eBook com TODAS as fórmulas (PDF). Ideal para imprimir e levar para a revisão final.
Função do 1º grau: coeficiente angular e gráfico
Modelo: \( f(x)=ax+b \). O coeficiente angular \(a\) indica crescimento ( \(a>0\) ) ou decrescimento ( \(a<0\) ); o termo \(b\) é o intercepto em \(y\).
Exemplo prático — receita de corrida por quilômetro
Enunciado. Um aplicativo paga \(f(x)=1{,}5x+4\) reais por corrida de \(x\) km. Quanto recebe-se em uma corrida de \(8\) km?
Ver solução passo a passo
Substitua \(x=8\):
\[ f(8) \;=\; 1{,}5\cdot 8 \\ =\; 12 \\ 12 + 4 \\ =\; 16 \text{ reais} \]Função do 2º grau: vértice, raízes e fórmula de Bhaskara
Modelo: \( f(x)=ax^2+bx+c \) com \(a\neq0\).
Discriminante: \( \Delta=b^2-4ac \). Raízes (quando existem): \( x=\dfrac{-b\pm\sqrt{\Delta}}{2a} \). Vértice: \( x_v=-\dfrac{b}{2a} \) e \( y_v=f(x_v) \).
Exemplo prático — altura máxima de um salto
Enunciado. A altura de um objeto é \(h(t)=-5t^2+20t+10\). Em que instante ocorre a altura máxima e qual é esse valor?
Ver solução passo a passo
O vértice dá o instante de altura máxima (parábola voltada para baixo, \(a=-5<0\)).
\[ t_v \;=\; -\dfrac{b}{2a} \\ =\; -\dfrac{20}{2\cdot(-5)} \\ =\; 2 \text{ s} \]Agora calcule \(h(2)\):
\[ h(2) \;=\; -5\cdot 2^2 \;+\; 20\cdot 2 \;+\; 10 \\ =\; -20 \;+\; 40 \;+\; 10 \\ =\; 30 \text{ m} \]Resposta: ocorre em \(2\) s e a altura máxima é \(30\) m.
Quer um atalho visual para revisar? Veja nossos Mapas Mentais de Matemática — versão enxuta para memorização rápida.
Potenciação: propriedades que aceleram cálculos
Para base \(a\neq0\) e expoentes \(x,y\):
\[ a^x\cdot a^y = a^{x+y} \qquad \dfrac{a^x}{a^y} = a^{x-y} \qquad (a^x)^y = a^{xy} \qquad a^0 = 1 \]Exemplo prático — simplificando sem calculadora
Enunciado. Simplifique \( \dfrac{2^7\cdot 2^3}{2^5} \).
Ver solução passo a passo
\[ 2^{7+3} \\ =\; 2^{10} \\ =\; 2^{10-5} \\ =\; 2^5 \\ =\; 32 \]Logaritmos: mudanças de base e propriedades
Definição: \( \log_a b = x \iff a^x=b \) (com \(a>0, a\neq1, b>0\)). Propriedades úteis:
\[ \log_a 1 = 0 \qquad \log_a a = 1 \qquad \log_a(bc)=\log_a b + \log_a c \qquad \log_a\!\left(\dfrac{b}{c}\right)=\log_a b – \log_a c \] \[ \log_a b = \dfrac{\log_c b}{\log_c a} \]Exemplo prático — somas de logaritmos
Enunciado. Calcule \( \log_{10} 25 + \log_{10} 4 \).
Ver solução passo a passo
\[ \log_{10} (25\cdot 4) \\ =\; \log_{10} 100 \\ =\; 2 \]Funções trigonométricas: período, amplitude e imagem
Para \(f(x)=a\sin(bx+c)\): amplitude \(=|a|\), período \(= \dfrac{2\pi}{|b|}\), imagem \(=[-\,|a|,\,|a|]\). Para \(g(x)=a\cos(bx+c)\), mesmas regras.
Exemplo prático — oscilação simples
Enunciado. Em \(y=3\sin(2x)\), determine amplitude e período.
Ver solução passo a passo
\[ \text{Amplitude} \;=\; |3| \\ =\; 3 \\ \text{Período} \;=\; \dfrac{2\pi}{|2|} \\ =\; \pi \]Áreas de figuras planas: o kit mínimo do ENEM
Quadrado
\[ A=a^2 \]Retângulo
\[ A=b\cdot h \]Trapézio
\[ A=\dfrac{(B+b)\cdot h}{2} \]Paralelogramo
\[ A=b\cdot h \]Sempre confira unidades (m, m², cm²). Em problemas com escala, converta antes de aplicar a fórmula.
Reforce sua preparação: visite a página ENEM Matemática, baixe os 10 eBooks e treine no Banco de Questões.
Lista de exercícios — resoluções com passo a passo
(1) Função do 1º grau
Enunciado. A função custo é \(C(x)=3x+120\). Qual é o custo para \(x=40\) unidades?
Mostrar solução
\[ C(40) \;=\; 3\cdot 40 \\ =\; 120 \\ 120 + 120 \\ =\; 240 \]Resposta: R\$ 240,00.
(2) Função do 2º grau
Enunciado. Resolva \(x^2-5x+6=0\).
Mostrar solução
\[ \Delta \;=\; b^2-4ac \\ =\; (-5)^2 – 4\cdot 1\cdot 6 \\ =\; 25 – 24 \\ =\; 1 \] \[ x \;=\; \dfrac{-b \pm \sqrt{\Delta}}{2a} \\ =\; \dfrac{5 \pm 1}{2} \\ x_1 \;=\; 3 \quad;\quad x_2 \;=\; 2 \](3) Potenciação
Enunciado. Simplifique \( (3^4\cdot 3^{-2})\cdot 3^5 \).
Mostrar solução
\[ 3^{4-2} \\ =\; 3^2 \\ 3^{2+5} \\ =\; 3^7 \](4) Logaritmos
Enunciado. Calcule \( \log_2 8 \).
Mostrar solução
\[ 2^x = 8 \\ 2^x = 2^3 \\ x = 3 \](5) Trigonometria
Enunciado. Qual a imagem de \(y=2\cos(x)\)?
Mostrar solução
\[ \text{Amplitude} \;=\; |2| \\ =\; 2 \\ \text{Imagem} \;=\; [-2,\; 2] \](6) Áreas
Enunciado. Um trapézio tem \(B=12\) cm, \(b=8\) cm e \(h=5\) cm. Calcule a área.
Mostrar solução
\[ A \;=\; \dfrac{(B+b)\cdot h}{2} \\ =\; \dfrac{(12+8)\cdot 5}{2} \\ =\; \dfrac{20\cdot 5}{2} \\ =\; \dfrac{100}{2} \\ =\; 50 \text{ cm}^2 \]Conclusão: como revisar essas fórmulas com eficiência
- Reconheça o modelo do enunciado antes de calcular.
- Escreva contas linha a linha para evitar erros.
- Monte um kit de revisão com o eBook de Fórmulas e os mapas mentais.
Perguntas frequentes
Quais fórmulas de matemática caem com mais frequência no ENEM?
As famílias mais cobradas são: funções do 1º e 2º grau (interpretação de gráficos e resolução de equações), potenciação, logaritmos, trigonometria básica e áreas de figuras planas. Domine modelos e pratique com questões.
Preciso decorar todas as fórmulas ou entender quando usar?
Entender o quando é decisivo. Memorize o mínimo e treine a identificação do modelo no enunciado. Ao reconhecer o tipo de problema, a aplicação da fórmula sai naturalmente.
Como evitar erros de sinal em Bhaskara e no vértice?
Escreva as etapas verticalmente, substituindo \(a\), \(b\) e \(c\) com parênteses. Calcule \(\Delta\) primeiro, depois aplique a fórmula, sempre conferindo o denominador \(2a\).
Qual a melhor forma de revisar na semana da prova?
Faça sessões curtas: releia o resumo, resolva 3 a 5 questões por tema e anote erros. Use os mapas mentais e o eBook de fórmulas para varrer tudo em menos de 40 minutos por dia.
Autor: Adriano Rocha — Blog Matemática Hoje.
Leituras relacionadas: Roteiro ENEM Matemática, Banco de Questões, Coleção 10 eBooks.





















