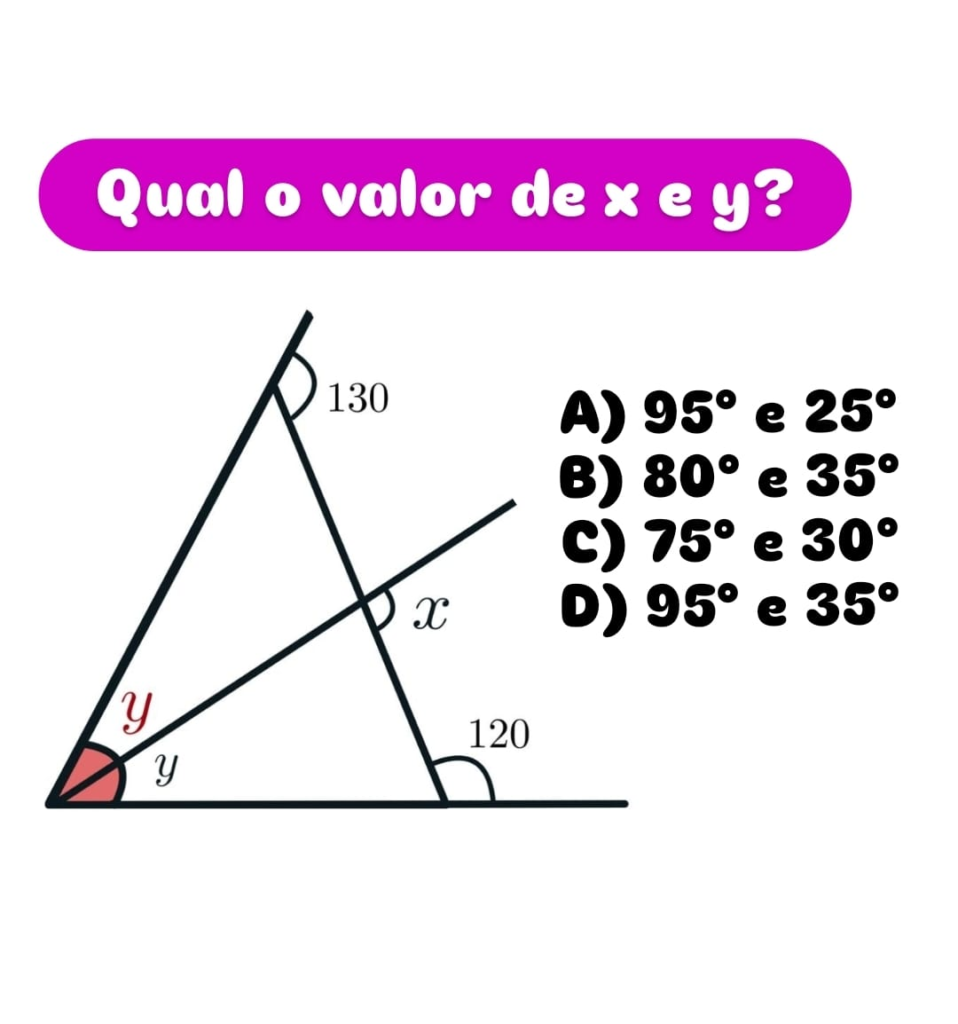
Em um triângulo, um dos ângulos externos mede 130° e o prolongamento da base forma um ângulo suplementar de 120° com o lado do triângulo. Sabendo que um segmento interno divide o triângulo em duas partes, formando dois ângulos internos x e y, determine o valor de x e y.
Pergunta:
Qual o valor de x e y?
Alternativas
A) 95° e 25°
B) 80° e 35°
C) 75° e 30°
D) 95° e 35°
Ver Solução
Solução
Relação dos ângulos externos e internos:
O ângulo externo de 130° é a soma dos ângulos internos adjacentes:
x + y = 130°
Diferença entre os ângulos:
A diferença entre xx e yy é dada como:
x − y = 60°
Sistema de Equações: Resolvendo as duas equações simultaneamente:
x+y=130°
x − y = 60°
Soma das equações:
(x + y) + (x − y) = 130° + 60°
2x = 190° ⟹ x = 95°
Substituindo x=95° na primeira equação:
95° + y = 130° ⟹ y = 35°
Resposta Final:
- x=95°
- y=35°
Alternativa D
