Análise Combinatória: Entenda as Fórmulas e Como Aplicá-las

A análise combinatória é uma área fundamental da matemática que estuda as formas de contar, organizar e agrupar elementos. Sua aplicação vai desde problemas cotidianos até questões mais complexas em concursos, estatística e probabilidade. Neste artigo, vamos explorar as principais fórmulas matemáticas da análise combinatória, explicar como usá-las e apresentar exemplos práticos.

O Que É Análise Combinatória?

A análise combinatória consiste em estudar maneiras de agrupar ou organizar objetos dentro de certos critérios. As três principais operações da análise combinatória são:

• Permutação: Organização de elementos em uma ordem específica.
• Arranjo: Agrupamento em que a ordem dos elementos importa.
• Combinação: Agrupamento de elementos sem se preocupar com a ordem.

Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!

Principais Fórmulas de Análise Combinatória

1 – Fórmulas Permutação

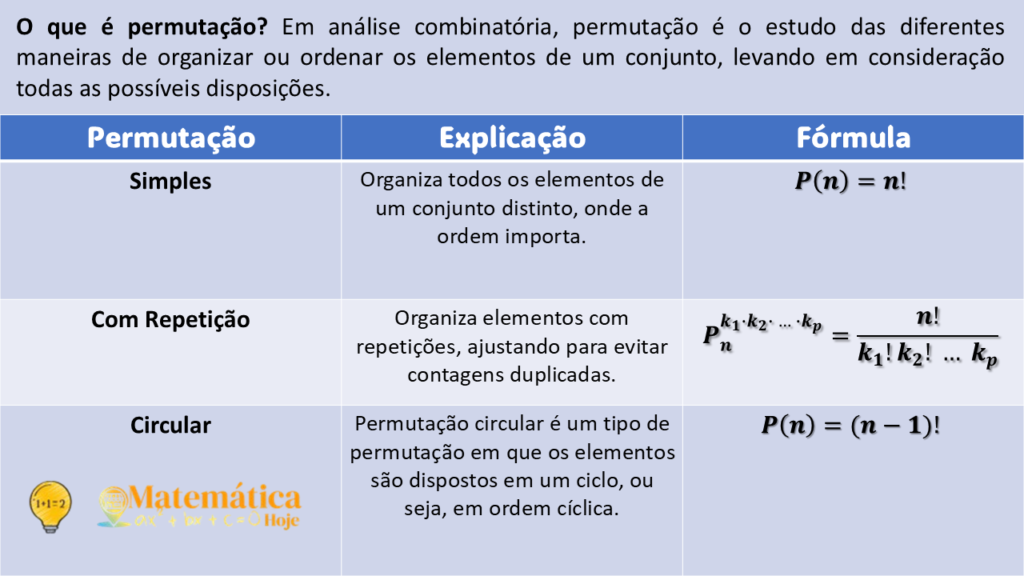
O que é permutação? Em análise combinatória, permutação é o estudo das diferentes maneiras de organizar ou ordenar os elementos de um conjunto, levando em consideração todas as possíveis disposições.

📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade

1.1 Fórmula de Permutação Simples

Permutação simples é o rearranjo ou ordenação de todos os elementos de um conjunto distinto, sem repetições. O número total de permutações simples de um conjunto com nnn elementos é dado pela fórmula do fatorial:

A permutação calcula o total de formas de organizar n elementos distintos.

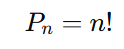
Onde:

• n! (fatorial de n) é o produto de todos os números inteiros positivos até n.

Exemplo 1: Quantas formas diferentes existem para organizar as letras da palavra “MÉTODO”?

P(6) = 6! =720

Exemplo 2:Considere um conjunto com três elementos: {A,B,C}. O número total de permutações é:

Solução: P(3) = 3! = 3⋅2⋅1 = 6

As possíveis permutações são:

1. ABC
2. ACB
3. BAC
4. BCA
5. CAB
6. CBA

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!

1.2 Fórmula Permutação com Repetição

Permutação com repetição ocorre quando em um conjunto há elementos repetidos, ou seja, nem todos os elementos são distintos. Nesse caso, o número de permutações é reduzido porque a troca entre elementos iguais não gera uma nova disposição.

A fórmula para calcular o número de permutações com repetição é:

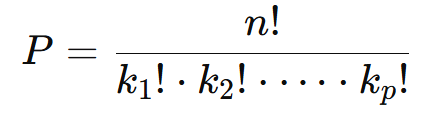
Onde:

• n é o número total de elementos no conjunto.
• k₁​, k₂​, …, k_p​ são as quantidades de repetições de cada tipo de elemento.

Explicação:

O denominador ajusta o total de permutações, eliminando as redundâncias causadas pelas repetições dos elementos.

Exemplo 1: Quantas formas existem de organizar as letras da palavra “MATEMATICA”?

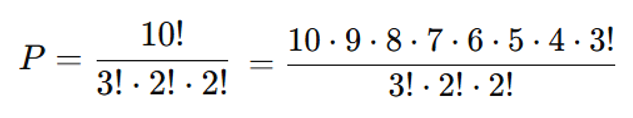
Exemplo 2: Considere a palavra BANANA. Ela tem 6 letras, mas algumas se repetem: 3 letras A, 2 letras N, e 1 letra B. O número de permutações com repetição é:

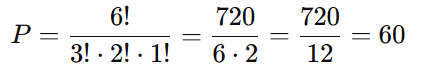
P = 151.200

1.3 Fórmula Permutação Circular

Permutação circular é um tipo específico de permutação em que os elementos de um conjunto são organizados em forma de círculo, de modo que a posição relativa entre os elementos importa, mas a rotação do círculo não é considerada uma nova permutação.

Diferentemente da permutação simples, onde o número de rearranjos possíveis de n elementos é dado por n!, em uma permutação circular o número de arranjos é reduzido porque as rotações são equivalentes. A fórmula para calcular o número de permutações circulares de n elementos é:

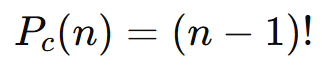
Explicação:

• Como em um círculo não há um ponto inicial fixo, uma permutação n! deve ser ajustada para excluir as disposições que apenas giram o círculo sem alterar a ordem relativa dos elementos. Isso resulta em (n – 1)!.

Exemplo: Se temos 4 pessoas (AA, B, C, D) que devem se sentar ao redor de uma mesa circular, o número de permutações é:

Pc(4) = (4 − 1)! = 3! = 3⋅2⋅1 = 6

As possíveis permutações seriam:

1. A – B – C – D
2. A – B – D – C
3. A – C – B – D
4. A – C – D – B
5. A – D – B – C
6. A – D – C – B

Nessa disposição, fixamos um elemento como referência (por exemplo, A) e organizamos os demais ao seu redor.

Veja também…

👉Entre no nosso canal do WhatsApp

📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito

2 – Fórmulas Arranjo

O que é Arranjo? Em análise combinatória, arranjo trata das diferentes formas de selecionar e ordenar k elementos de um conjunto com n elementos distintos, considerando a ordem dos elementos como relevante. Em um arranjo, a posição dos elementos faz diferença, ou seja, trocar a ordem de dois elementos gera um novo arranjo.

2.1 Fórmula de Arranjo Simples

Arranjo Simples é um conceito de análise combinatória que representa o número de maneiras de selecionar e ordenar k elementos de um conjunto de n elementos distintos, levando em consideração a ordem dos elementos escolhidos.

A fórmula do arranjo é dada por:

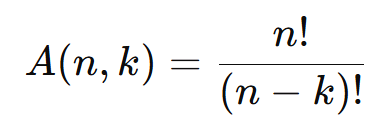
Onde:

• n: número total de elementos no conjunto;
• k: número de elementos selecionados;
• n!: fatorial de n;
• (n − k)!: fatorial da diferença entre n e k.

Exemplo: Se temos 4 livros (A, B, C, D) e queremos organizar 2 deles em uma estante, o número de arranjos possíveis é:

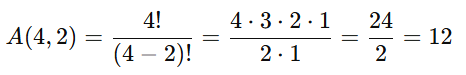
Os arranjos possíveis são:

• AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, DC

Aqui, a troca na ordem dos livros AB e BA resulta em arranjos diferentes.

Diferença entre Arranjo e Combinação (próximo tema):

• No arranjo, a ordem dos elementos importa.
• Na combinação, a ordem dos elementos não importa.

2.2 Fórmula de Arranjo com Repetição

Arranjo com repetição é um conceito da análise combinatória em que se selecionam k elementos de um conjunto com n elementos distintos, permitindo que o mesmo elemento seja escolhido mais de uma vez, e a ordem dos elementos importa.

Formula Arranjo com Repetição

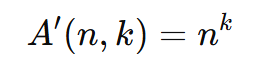
Onde:

• n: número total de elementos no conjunto;
• k: número de elementos a serem escolhidos;
• n^k: número total de arranjos possíveis, permitindo repetições.

Exemplo: Considere um conjunto com 3 elementos: {A, B, C}. Se quisermos formar arranjos de 2 elementos, permitindo repetições:

A′(3, 2) = 3² = 9

Os arranjos possíveis são:

• AA, AB, AC, BA, BB, BC, CA, CB, CC

Aqui, um mesmo elemento (por exemplo, A) pode aparecer mais de uma vez no arranjo, e a ordem é relevante (AB ≠ BA).

Diferença entre Arranjo Simples e Arranjo com Repetição:

• No arranjo simples, os elementos não podem ser repetidos.
• No arranjo com repetição, os elementos podem ser escolhidos mais de uma vez.

Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!

3 – Fórmulas Combinação

O que é Combinação? Combinação é um conceito da análise combinatória que representa o número de maneiras de selecionar k elementos de um conjunto com n elementos distintos, sem levar em conta a ordem dos elementos escolhidos. Ou seja, na combinação, a ordem dos elementos não altera o resultado.

3.1 Fórmula de Combinação Simples

Combinação simples é um caso particular da análise combinatória em que se calcula o número de formas de selecionar k elementos de um conjunto de n elementos distintos, sem considerar a ordem dos elementos selecionados.

Fórmula da Combinação Simples:

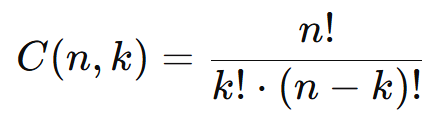
Onde:

• n: número total de elementos no conjunto;
• k: número de elementos escolhidos;
• n!: fatorial de n (o produto de todos os números inteiros positivos de 1 até n);
• k!: fatorial de k, que ajusta as redundâncias pela ordem das escolhas;
• (n – k)!: fatorial da diferença entre n e k.

Exemplo: Considere um grupo de 6 pessoas: {A, B, C, D, E, F}. Queremos formar uma equipe de 3 pessoas.

Solução: O número de combinações simples é:

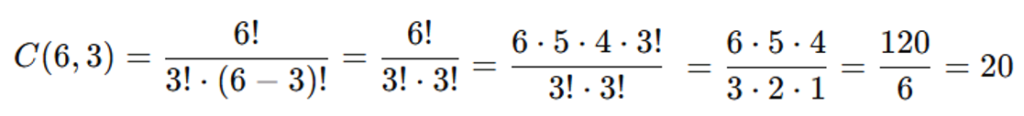
Portanto, existem 20 combinações simples possíveis para formar uma equipe de 3 pessoas.

3.2 Fórmula da Combinação Composto:

A combinação composta, também chamada de combinação com repetição, é um conceito da análise combinatória que trata do número de formas de selecionar k elementos de um conjunto com n elementos distintos, permitindo repetições e sem considerar a ordem dos elementos escolhidos.

Fórmula da Combinação Composta:

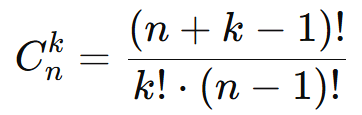
Onde:

• n: número total de elementos no conjunto original;
• k: número de elementos a serem selecionados (podendo ser maior que n);
• 1n + k – 1: ajuste para permitir repetições;
• k!: fatorial do número de elementos selecionados;
• (n – 1)!: fatorial do número de elementos originais ajustado para repetição.

Características:

• Permite repetição: um mesmo elemento do conjunto pode ser escolhido mais de uma vez.
• A ordem não importa: seleções como ABABAB e BABABA são consideradas iguais.
• É usada em problemas onde itens podem ser reutilizados, como a escolha de moedas ou recursos repetíveis.

Exemplo: Imagine que você tem 3 tipos de frutas (n = 3): maçã (M), banana (B), e laranja (L), e deseja escolher 4 frutas (k = 4), permitindo repetições.

O número de combinações compostas é:

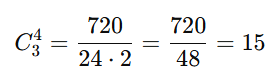
Portanto, existem 15 formas distintas de escolher 4 frutas permitindo repetições. Por exemplo:

• MMMB, MMML, MBBB, MBLL, etc.

A combinação composta é amplamente utilizada em problemas que envolvem recursos reutilizáveis, como formação de equipes, escolhas com reposição ou agrupamento de itens repetidos.

Baixe o e-book gratuito Formulas Matemática

Dicas para Memorizar as Fórmulas de Análise Combinatória

1. Pratique Regularmente: Resolva muitos problemas práticos envolvendo permutações, combinações e arranjos.
2. Associe a Exemplos Reais: Relacione as fórmulas com situações do dia a dia, como organização de objetos ou seleção de equipes.
3. Use Diagramas e Representações Visuais: Isso ajuda a visualizar os conceitos.

Aplicações da Análise Combinatória

A análise combinatória tem aplicações amplas, incluindo:

• Probabilidade: Cálculo de eventos prováveis.
• Concursos e Vestibulares: Questões sobre organização e seleção de elementos.
• Ciência da Computação: Análise de algoritmos e estruturas de dados.
• Gestão e Logística: Planejamento de rotas e organização de tarefas.

Confira também as formulas geometria espacial

Exemplo de Uso Prático: Probabilidade e Análise Combinatória

Imagine que você tem uma loteria onde deve escolher 6 números entre 60. Quantas combinações são possíveis?

C₆₀,₆ = 60![6!⋅(60−6)!] = 50.063.860

Isso significa que existem mais de 50 milhões de combinações possíveis, evidenciando a importância da análise combinatória em cenários reais.

Conclusão

Dominar as fórmulas matemáticas de análise combinatória é essencial para resolver questões envolvendo contagem, organização e probabilidade. veja também a fórmula de bhaskara. Com a prática, você estará preparado para aplicar esses conceitos em diversas situações, desde provas até problemas do cotidiano. Continue praticando e explorando as possibilidades que a matemática oferece!