A função potência é um tipo de função fundamental na Matemática, amplamente aplicada na física, economia, engenharia e em diversas áreas do conhecimento. Compreendê-la é essencial para o estudo de funções mais complexas e para o desenvolvimento do raciocínio matemático.
O que é uma Função Potência?
Chamamos de função potência toda função real da forma:
f(x) = a · xⁿ
- a é um número real (coeficiente);
- n é um número real (expoente);
- x é a variável independente.
Quando n é inteiro e positivo, temos uma função polinomial. Se for negativo ou fracionário, a função pode representar um comportamento racional ou com raízes.
Classificações da Função Potência
- n ∈ ℕ: Ex: f(x) = x², f(x) = 3x³
- n = 0: f(x) = a (função constante)
- n < 0: f(x) = x⁻¹ (comportamento racional)
- n fracionário: f(x) = x^(1/2) (raízes)
Gráficos de Funções Potência
O formato do gráfico depende do valor de n:
- n par: gráfico simétrico em relação ao eixo y.
- n ímpar: gráfico simétrico em relação à origem.
- n negativo: gráfico com assíntotas nos eixos.
- n fracionário: pode representar raízes (x ≥ 0 se par).
Exemplos de Função Potência
Exemplo 1:
f(x) = 2x³
Função crescente, definida para todos os reais. Passa pela origem.
Exemplo 2:
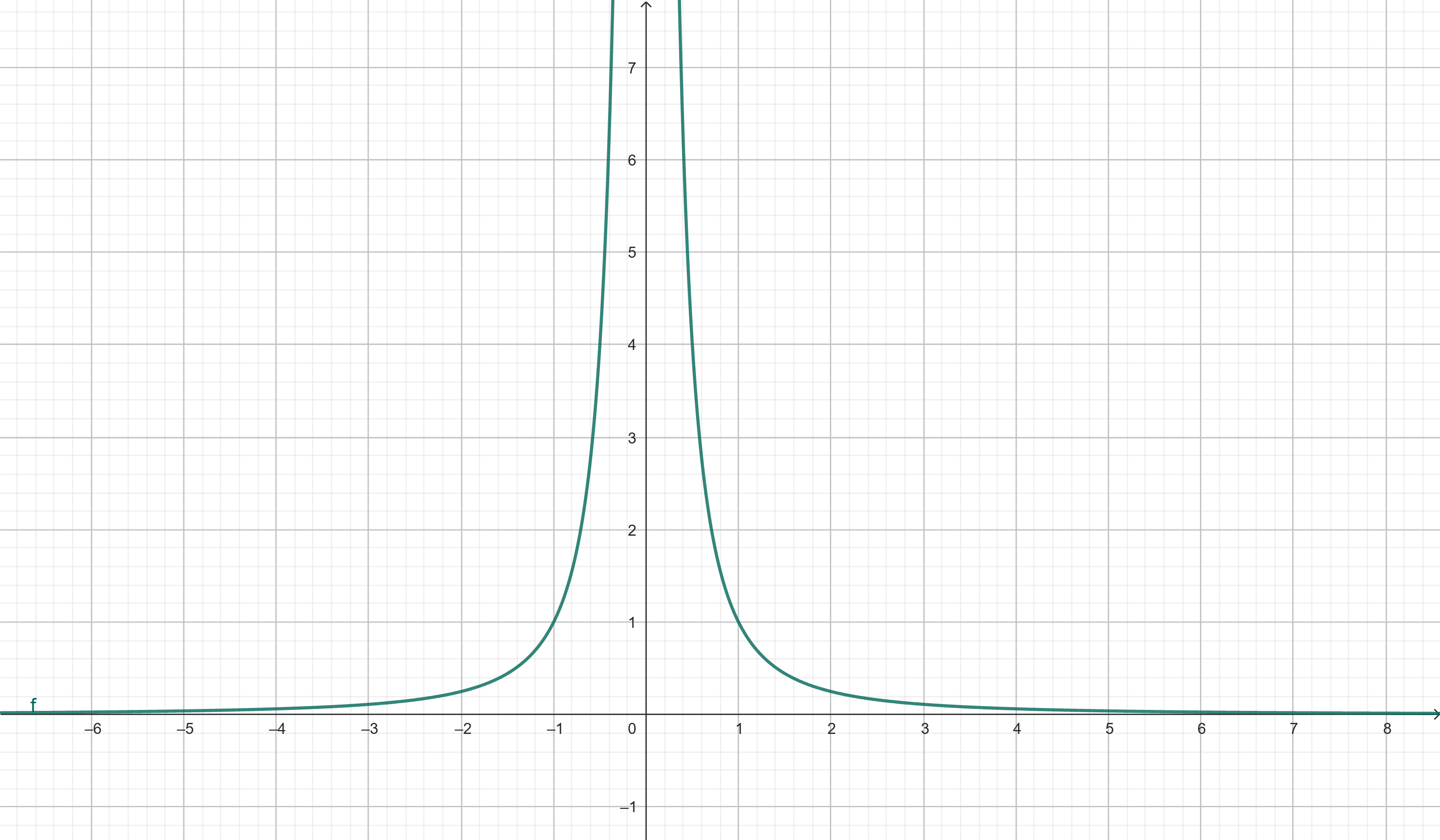
f(x) = x⁻²
Indefinida em x = 0. O gráfico possui assíntotas nos eixos.
Exemplo 3:
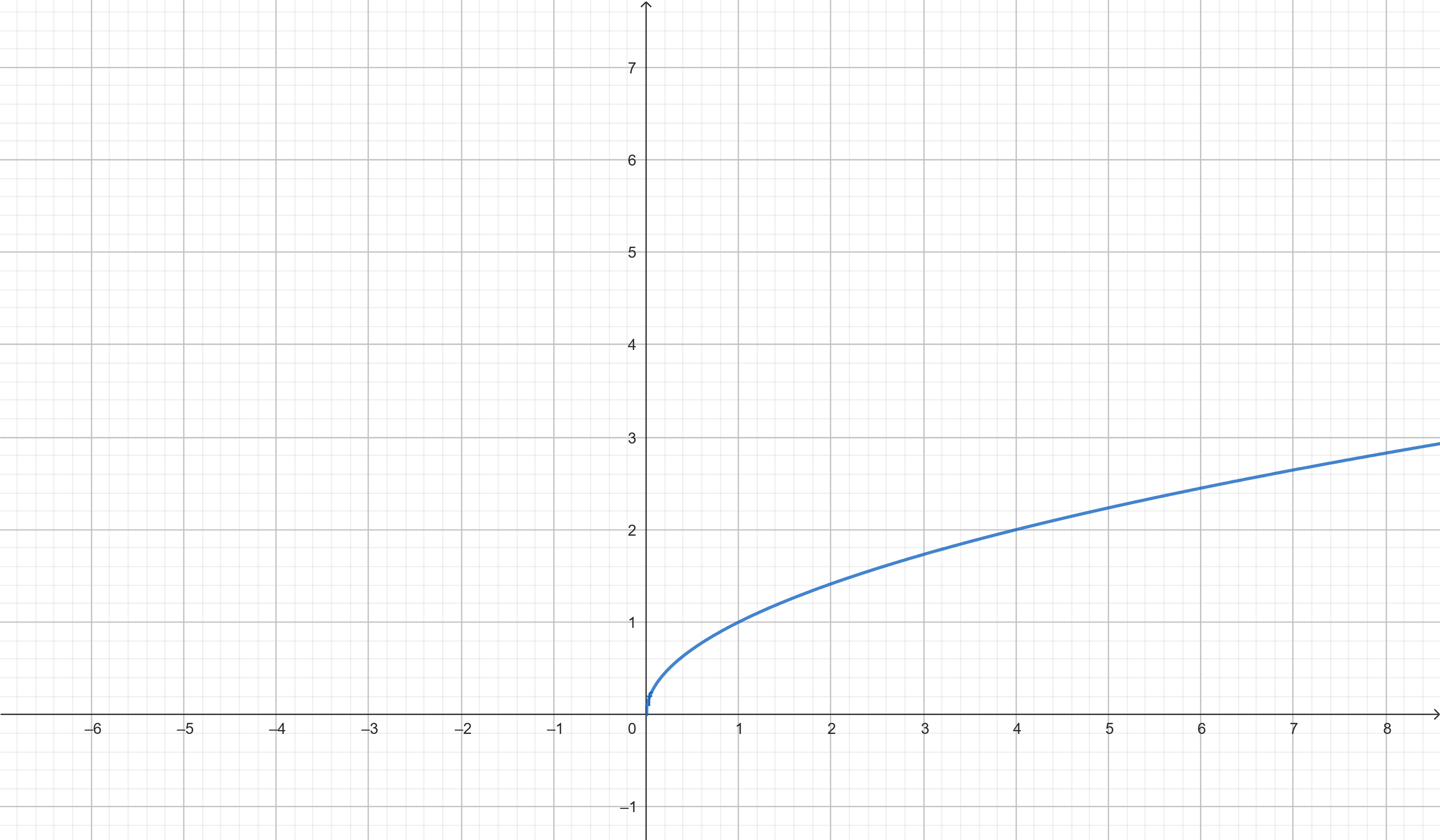
f(x) = √x
Função raiz quadrada. Domínio: x ≥ 0.
Propriedades Importantes
- f(x) = xⁿ é par se n é par: f(-x) = f(x)
- f(x) = xⁿ é ímpar se n é ímpar: f(-x) = -f(x)
- O domínio depende do valor de n
- O sinal depende do coeficiente e do expoente
Exercícios Resolvidos
Exercício 1
Determine o valor de f(2) para f(x) = 3x²
Solução:
f(2) = 3·(2)² = 3·4 = 12
Exercício 2
Considere f(x) = x⁻¹. Determine f(1), f(2) e f(0,5)
Solução:
f(1) = 1⁻¹ = 1
f(2) = 2⁻¹ = 1/2
f(0,5) = (1/2)⁻¹ = 2
Exercício 3
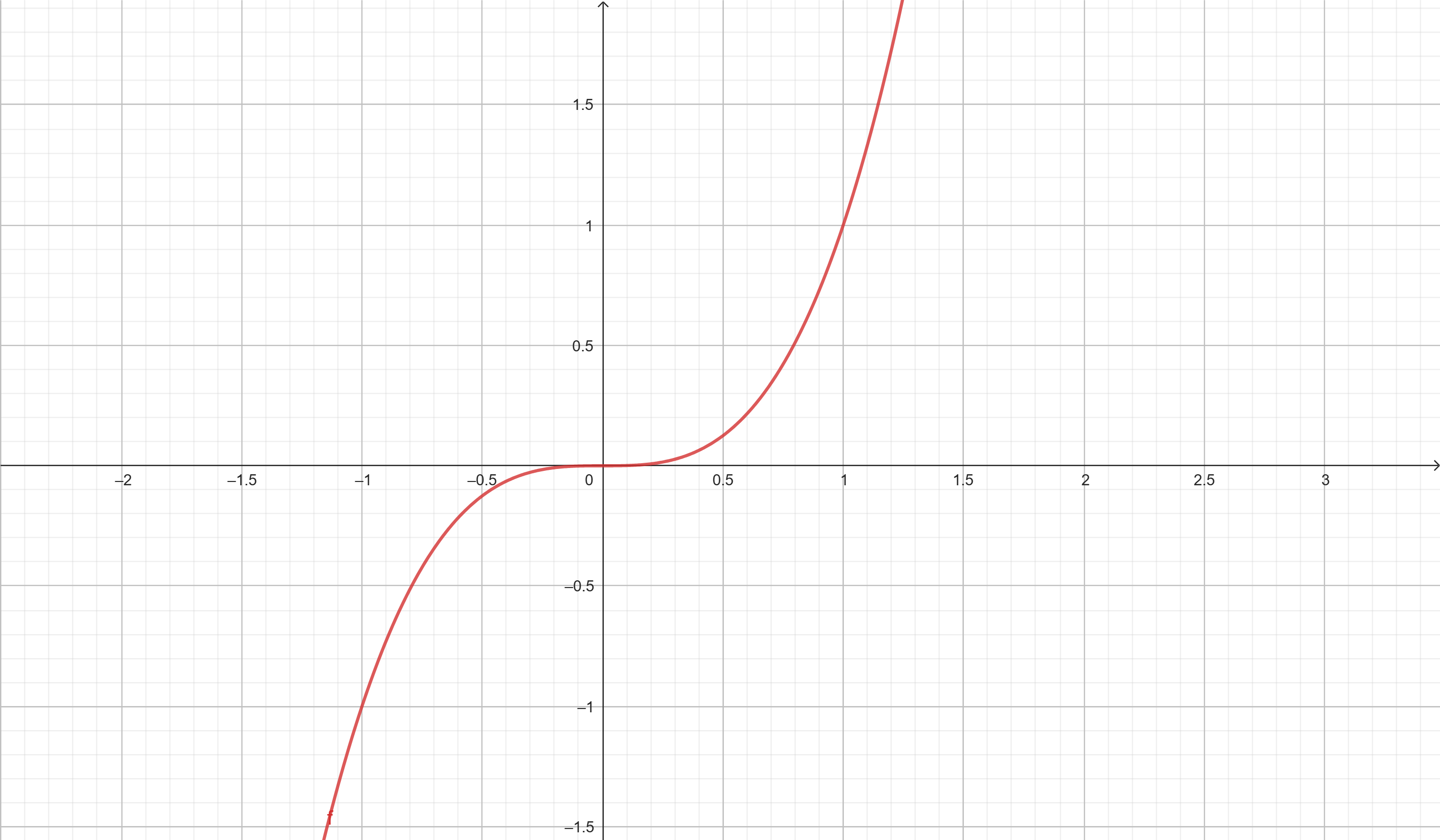
Esboce o gráfico de f(x) = x³
Pontos importantes: f(-2) = -8, f(0) = 0, f(2) = 8
Exercício 4
Para quais valores de x a função f(x) = x^(1/2) está definida?
Solução:
Como é uma raiz quadrada, o domínio é x ≥ 0
Exercício 5
Classifique como par, ímpar ou nenhuma: f(x) = -x⁴
Solução:
f(-x) = -(-x)⁴ = -x⁴ = f(x), logo, função par
Conclusão
A função potência é essencial para o domínio de conceitos fundamentais da matemática. Com ela, é possível entender melhor funções polinomiais, exponenciais e muitos outros tópicos importantes.






















