Aprenda tudo sobre funções matemáticas com esta lista completa de 12 questões resolvidas passo a passo. As atividades abordam situações do dia a dia com triângulos, quadrados, vendas, redes sociais e muito mais — ideais para quem estuda função afim, domínio, interpretação de gráficos e formulação de expressões matemáticas.
Perfeita para alunos do ensino fundamental II, ensino médio ou para reforço escolar, essa coletânea traz aplicações práticas, exercícios com tabelas e desafios com lógica e criatividade.
👉 Veja como utilizar palitos de fósforo para criar funções, resolver problemas e compreender melhor o conceito de variável dependente e independente.
🧠 Mapas Mentais de MatemáticaConteúdo: Análise de Relações entre Variáveis – Variável Dependente e Independente
Questão 01. Nos itens a seguir, estão descritas algumas relações entre variáveis. Em cada caso, identifique a variável independente e a variável dependente.
a) O número de barras de chocolate que alguém compra e a quantia paga por elas.
b) O andar do apartamento em que uma pessoa mora e o tempo necessário para o elevador, a partir do térreo e sem nenhuma parada, chegar até o apartamento.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos analisar as relações entre duas variáveis em cada item e identificar qual é a causa (independente) e qual é o efeito (dependente).
a) Número de barras de chocolate e quantia paga.
• Variável independente: número de barras de chocolate (é o que escolhemos livremente).
• Variável dependente: quantia paga (depende da quantidade comprada).
b) Andar do apartamento e tempo para o elevador chegar.
• Variável independente: andar do apartamento (é o que determina o tempo).
• Variável dependente: tempo necessário para o elevador chegar (depende da altura/andar).
✅ Conclusão:
a) Independente: número de barras de chocolate — Dependente: quantia paga
b) Independente: andar do apartamento — Dependente: tempo para o elevador chegar
Conteúdo: Identificação de Função Algébrica a partir de Tabelas
Questão 02. (Saresp-SP) As variáveis \( s \) e \( t \) estão relacionadas de acordo com a tabela a seguir:
| t | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| s | 0 | 3 | 8 | 15 | 24 |
A relação algébrica entre \( s \) e \( t \) é:
a) \( s = 2t – 2 \) b) \( s = t – 1 \) c) \( s = t^2 – 1 \) d) \( s = t^2 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A tabela relaciona os valores de \( t \) com os valores correspondentes de \( s \). Nosso objetivo é descobrir qual das expressões fornecidas representa corretamente essa relação.
1) Testando a alternativa A: \( s = 2t – 2 \)
Para \( t = 1 \Rightarrow s = 0 \) ✅
Para \( t = 2 \Rightarrow s = 2 \) ❌ (esperado: 3)
2) Testando a alternativa B: \( s = t – 1 \)
Para \( t = 1 \Rightarrow s = 0 \) ✅
Para \( t = 2 \Rightarrow s = 1 \) ❌
3) Testando a alternativa C: \( s = t^2 – 1 \)
- Para \( t = 1 \Rightarrow s = 1^2 – 1 = 0 \) ✅
- Para \( t = 2 \Rightarrow s = 4 – 1 = 3 \) ✅
- Para \( t = 3 \Rightarrow s = 9 – 1 = 8 \) ✅
- Para \( t = 4 \Rightarrow s = 16 – 1 = 15 \) ✅
- Para \( t = 5 \Rightarrow s = 25 – 1 = 24 \) ✅
4) Testando a alternativa D: \( s = t^2 \)
Para \( t = 1 \Rightarrow s = 1 \) ❌ (esperado: 0)
✅ Conclusão: A relação correta entre as variáveis é c) \( s = t^2 – 1 \)
🧠 Mapas Mentais de MatemáticaConteúdo: Funções algébricas – Expressões em função de uma variável
Questão 03. O retângulo representado na figura tem lados que medem \( x \) e \( 2x \).
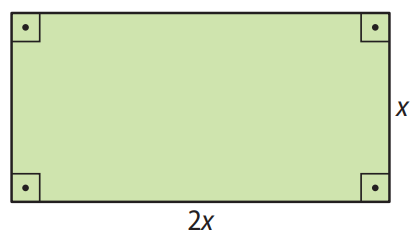
Expresse o perímetro \( P \), a área \( A \) e a medida \( d \) da diagonal desse retângulo em função de \( x \).
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
O retângulo possui base igual a \( 2x \) e altura igual a \( x \). Vamos usar fórmulas conhecidas de geometria para expressar as grandezas pedidas em função de \( x \).
1) Perímetro:
A fórmula do perímetro de um retângulo é:
$$ P = 2 \cdot (2x + x) = 2 \cdot 3x = \mathbf{6x} $$
2) Área:
A fórmula da área de um retângulo é:
$$ A = 2x \cdot x = \mathbf{2x^2} $$
3) Diagonal:
Aplicando o Teorema de Pitágoras:
$$ d = \sqrt{(2x)^2 + x^2} = \sqrt{4x^2 + x^2} = \sqrt{5x^2} = \mathbf{x\sqrt{5}} $$
✅ Conclusão:
- Perímetro: \( P = 6x \)
- Área: \( A = 2x^2 \)
- Diagonal: \( d = x\sqrt{5} \)
Conteúdo: Função Afim – Determinação dos coeficientes
Questão 04. Arthur elaborou uma fórmula em uma planilha de cálculo e usou a lei geral \( y = ax + b \), em que \( a \) e \( b \) são números inteiros. Em seguida, anotou alguns dos valores obtidos, como indicado a seguir:
| x (nº de entrada) | y (nº de saída) |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 4 | 11 |
| 5 | 13 |
Com base nessas informações, determine os valores de \( a \) e \( b \) e escreva a fórmula utilizada por Arthur.
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A tabela mostra os pares ordenados \((x, y)\). Sabemos que a função é do tipo \( y = ax + b \). Vamos utilizar os dados da tabela para encontrar os coeficientes \( a \) e \( b \).
1) Identificando o coeficiente \( a \):
Observe o crescimento do valor de \( y \) quando \( x \) aumenta de 1 em 1:
De \( y = 3 \) para \( y = 5 \): aumento de 2
De \( y = 5 \) para \( y = 7 \): aumento de 2
Portanto, o coeficiente angular é:
$$ a = 2 $$
2) Identificando o coeficiente \( b \):
Sabemos que quando \( x = 0 \), \( y = 3 \). Isso nos dá diretamente o valor de \( b \):
$$ b = 3 $$
3) Montando a função:
Substituindo \( a \) e \( b \) na expressão geral:
$$ y = 2x + 3 $$
✅ Conclusão:
- Coeficiente angular: \( a = 2 \)
- Coeficiente linear: \( b = 3 \)
- Função final: \( y = 2x + 3 \)
Conteúdo: Função – Modelagem de situações do cotidiano
Questão 05. (UFG-GO) Um padeiro fabrica 300 pães por hora. Considerando esse dado, pede-se:
a) a lei que representa o número de pães fabricados (\( p \)) em função do tempo (\( t \));
b) quantos pães são fabricados em 3 horas e 30 minutos?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
O problema nos informa que a produção é de 300 pães por hora. Precisamos montar uma função que relacione a produção total \( p \) ao tempo em horas \( t \).
1) Determinando a função:
Como são produzidos 300 pães por hora, a função será do tipo:
$$ p(t) = 300t $$
2) Calculando a produção em 3 horas e 30 minutos:
Precisamos transformar 3 horas e 30 minutos em horas decimais:
$$ t = 3 + \frac{30}{60} = 3{,}5 $$
Substituindo na função:
$$ p(3{,}5) = 300 \cdot 3{,}5 = 1050 $$
✅ Conclusão:
- Função: \( p(t) = 300t \)
- Produção em 3h30min: \( 1050 \) pães
Conteúdo: Conjunto Imagem de Funções
Questão 06. Dado o conjunto \( A = \{-2, -1, 0, 1\} \), determine o conjunto imagem da função \( f: A \rightarrow \mathbb{R} \) quando \( f \) for definida por:
a) \( f(x) = x^3 \)
b) \( f(x) = -x + 3 \)
c) \( f(x) = 1 – x^2 \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Vamos aplicar cada função aos elementos do conjunto \( A = \{-2, -1, 0, 1\} \) e identificar os respectivos valores de saída, formando assim o conjunto imagem.
a) \( f(x) = x^3 \)
\( f(-2) = (-2)^3 = -8 \)
\( f(-1) = (-1)^3 = -1 \)
\( f(0) = 0^3 = 0 \)
\( f(1) = 1^3 = 1 \)
Imagem: \( \text{Im}(f) = \{-8, -1, 0, 1\} \)
b) \( f(x) = -x + 3 \)
\( f(-2) = -(-2) + 3 = 2 + 3 = 5 \)
\( f(-1) = -(-1) + 3 = 4 \)
\( f(0) = -0 + 3 = 3 \)
\( f(1) = -1 + 3 = 2 \)
Imagem: \( \text{Im}(f) = \{2, 3, 4, 5\} \)
c) \( f(x) = 1 – x^2 \)
\( f(-2) = 1 – 4 = -3 \)
\( f(-1) = 1 – 1 = 0 \)
\( f(0) = 1 – 0 = 1 \)
\( f(1) = 1 – 1 = 0 \)
Imagem: \( \text{Im}(f) = \{-3, 0, 1\} \)
✅ Conclusão:
- a) \( \text{Im}(f) = \{-8, -1, 0, 1\} \)
- b) \( \text{Im}(f) = \{2, 3, 4, 5\} \)
- c) \( \text{Im}(f) = \{-3, 0, 1\} \)
Conteúdo: Identificação da lei de formação a partir de diagramas de funções
Questão 07. Os diagramas de flechas a seguir indicam o domínio e o conjunto imagem de uma função. Em cada caso, escreva uma possível lei de formação da função.
a) Função \( f \):
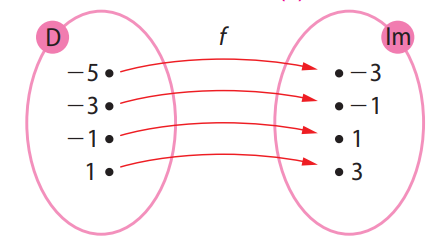
b) Função \( h \):
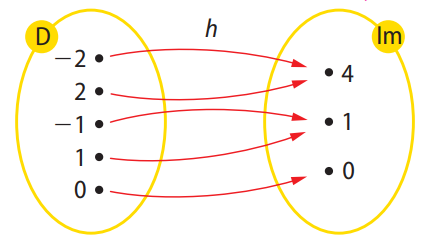
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Vamos analisar os pares \((x, y)\) representados nas setas dos diagramas para descobrir uma regra (lei de formação) que relacione \( x \) com \( y \).
a) Função \( f \)
Observando os pares:
\( f(-5) = -3 \)
\( f(-3) = -1 \)
\( f(-1) = 1 \)
\( f(1) = 3 \)
A variação mostra que estamos somando 2 ao valor de \( x \):
$$ f(x) = x + 2 $$
b) Função \( h \)
Observando os pares:
\( h(-2) = 4 \)
\( h(-1) = 1 \)
\( h(0) = 0 \)
\( h(1) = 1 \)
\( h(2) = 4 \)
Note que estamos elevando \( x \) ao quadrado:
$$ h(x) = x^2 $$
✅ Conclusão:
- a) \( f(x) = x + 2 \)
- b) \( h(x) = x^2 \)
Conteúdo: Função Afim – Interpretação de Problemas com Tabela
Questão 8. (EPCAR-MG) Um pintor foi contratado para pintar a fachada do prédio do Comando da Epcar, em decorrência das comemorações do seu sexagésimo aniversário. Esse pintor cobra um valor fixo de 30 reais e mais uma quantia que depende da área pintada. A tabela seguinte indica o orçamento apresentado pelo pintor.
| Área x pintada (em m²) | Total a pagar pela pintura (em reais) incluindo a parcela fixa |
|---|---|
| 5 | 40 |
| 10 | 50 |
| 15 | 60 |
| 20 | 70 |
| 30 | 90 |
| 40 | 110 |
Com base nos dados acima, classifique em (V) verdadeiro ou (F) falso cada item a seguir.
- O pintor cobra 30 reais mais 3 reais pelo metro quadrado pintado.
- Se foram pagos pela pintura 530 reais, então a área pintada foi de 250 m².
- Pela pintura de uma área correspondente a 150 m² seria cobrado menos de 300 reais.
Tem-se a sequência correta em:
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A questão envolve uma função afim na qual o valor cobrado é composto por uma parcela fixa e outra proporcional à área. Devemos descobrir se os valores fornecidos são coerentes com a fórmula da função e com os cálculos pedidos.
1) Descobrindo a função:
Com base na tabela, por exemplo, quando a área é 10 m², o total é R$50, ou seja:
$$ 30 + 10 \cdot x = 50 \Rightarrow x = 2 $$
Mas testando com 20 m², temos R$70. Logo:
$$ 30 + 20 \cdot x = 70 \Rightarrow x = 2 $$
Portanto, a função correta é:
$$ f(x) = 30 + 2x $$
2) Analisando as afirmações:
- Afirmação 1: Diz que o pintor cobra R$30 + R$3 por metro quadrado, mas vimos que ele cobra R$2 por metro quadrado. Falsa.
- Afirmação 2: Se foram pagos R$530:
- Afirmação 3: Área de 150 m²:
$$ 530 = 30 + 2x \Rightarrow 2x = 500 \Rightarrow x = 250 $$
Logo, Verdadeira.
$$ f(150) = 30 + 2 \cdot 150 = 330 $$
330 é maior que 300. Falsa.
✅ Conclusão:
- Afirmação 1: Falsa
- Afirmação 2: Verdadeira
- Afirmação 3: Falsa
Sequência: F – V – F
Portanto, a alternativa correta é a letra c).
Alternativa correta: c) F – V – V
🧠 Mapas Mentais de MatemáticaConteúdo: Domínio de Funções – Funções Racionais, Polinomiais e com Raiz Quadrada
Questão 9. Determine o domínio das funções definidas por:
a) \( h(x) = 4x – 5 \)
b) \( j(x) = \dfrac{3}{1 + x} \)
c) \( z(x) = \sqrt{2x} \)
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Devemos determinar os valores de \( x \) para os quais cada função está definida, ou seja, identificar o domínio de cada expressão.
a) Função polinomial: \( h(x) = 4x – 5 \)
Funções polinomiais estão definidas para todos os valores reais.
$$ D(h) = \mathbb{R} $$
b) Função racional: \( j(x) = \dfrac{3}{1 + x} \)
A função está indefinida quando o denominador é zero:
$$ 1 + x = 0 \Rightarrow x = -1 $$
Então, excluímos esse valor do domínio.
$$ D(j) = \mathbb{R} \setminus \{-1\} $$
c) Função com raiz: \( z(x) = \sqrt{2x} \)
A raiz quadrada só está definida para valores maiores ou iguais a zero:
$$ 2x \geq 0 \Rightarrow x \geq 0 $$
Assim:
$$ D(z) = \{x \in \mathbb{R} \mid x \geq 0\} $$
✅ Conclusão:
- Domínio de \( h(x) \): \( \mathbb{R} \)
- Domínio de \( j(x) \): \( \mathbb{R} \setminus \{-1\} \)
- Domínio de \( z(x) \): \( \{x \in \mathbb{R} \mid x \geq 0\} \)
Conteúdo: Função – Formação de Triângulos com Palitos
Questão 10. Observe a sequência de triângulos cujos lados são formados por palitos de fósforo.
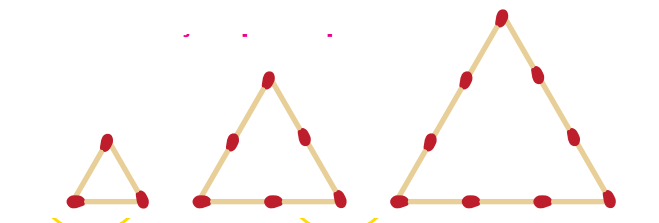
a) Reproduza o quadro e complete-o com os valores que faltam.
| Número de palitos em cada lado | Total de palitos em cada triângulo |
|---|---|
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
| 4 | 12 |
| 5 | 15 |
| 6 | 18 |
b) Considere \( x \) o número de palitos em cada lado e \( y \) o total de palitos em cada triângulo para escrever uma sentença matemática que expresse \( y \) em função de \( x \).
c) Qual é o domínio dessa função? E o conjunto imagem?
d) Quantos palitos deve ter cada lado para se construir um triângulo com 45 palitos?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Cada triângulo é formado por 3 lados com o mesmo número de palitos. Portanto, o total de palitos é o triplo do número de palitos de um lado.
Função matemática:
Se \( x \) é o número de palitos por lado, então:
$$ y = 3x $$
c) Domínio e imagem:
- Domínio: \( \mathbb{N}^* \) (números naturais positivos)
- Imagem: \( \{ y \in \mathbb{N}^* \mid y \equiv 0 \pmod{3} \} \) = {3,6,9,12,15,18,…}
d) Encontrando x para y = 45:
$$ y = 3x \Rightarrow 45 = 3x \Rightarrow x = 15 $$
Resposta: Cada lado deve ter 15 palitos.
🧠 Mapas Mentais de MatemáticaConteúdo: Função – Sequência com Quadrados de Palitos de Fósforo
Questão 11. Com base na ideia da atividade anterior sobre triângulos com palitos , elabore um problema considerando uma sequência formada por quadrados construídos com palitos de fósforo.
Troque o problema com um colega para que um resolva o problema elaborado pelo outro.
Exemplo de problema proposto:
Observe a sequência de figuras formadas por quadrados, todos construídos com palitos de fósforo:
a) Complete a tabela abaixo com o número total de palitos em cada figura:
| Número de quadrados | Total de palitos |
|---|---|
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
| 4 | 13 |
| 5 | 16 |
b) Escreva uma função que relacione o número de quadrados \( x \) com o total de palitos \( y \).
c) Qual será o número total de palitos em uma sequência de 30 quadrados?
d) Qual é o domínio e o conjunto imagem dessa função?
🔍 Ver solução passo a passo
🔎 Entendendo o padrão:
A cada novo quadrado, acrescentam-se 3 palitos (pois 1 lado é compartilhado com o anterior).
1 quadrado: 4 palitos
2 quadrados: 4 + 3 = 7
3 quadrados: 7 + 3 = 10, e assim por diante.
Função:
$$ y = 3x + 1 $$
Resposta do item c:
Para \( x = 30 \):
$$ y = 3 \cdot 30 + 1 = 91 $$
Resposta do item d:
- Domínio: \( \mathbb{N}^* \), pois o número de quadrados deve ser natural e positivo.
- Imagem: \( \{4, 7, 10, 13, 16, \dots\} \) – sequência crescente com razão 3 e primeiro termo 4.
Conteúdo: Função Afim – Aplicação com Redes Sociais e Vendas
Questão 12. O gerente de uma loja de eletrônicos verificou que, quanto mais ele anuncia em redes sociais, mais itens a loja vende. Essa relação pode ser expressa por uma função dada pela lei:
$$ y = \frac{3}{2}x + 80 $$
Em que y representa o número de itens vendidos durante a semana e x, o número de anúncios publicados no mesmo período.
Nessas condições, quantas vezes o gerente deverá anunciar em uma semana para que a loja venda 200 itens?
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
A função relaciona o número de anúncios \( x \) com a quantidade de vendas \( y \). Queremos saber o valor de \( x \) que torna \( y = 200 \).
1) Substituindo y por 200:
$$ 200 = \frac{3}{2}x + 80 $$
2) Isolando x:
$$ 200 – 80 = \frac{3}{2}x $$
$$ 120 = \frac{3}{2}x $$
$$ x = \frac{120 \cdot 2}{3} = 80 $$
✅ Resposta final: O gerente deverá anunciar 80 vezes na semana.
🧠 Mapas Mentais de Matemática



























