Uma lanchonete recebeu uma encomenda de 65 copos de sucos de frutas. Até 3 sabores podem ser misturados em cada copo: abacaxi, laranja e morango. O diagrama a seguir representa algumas quantidades produzidas de cada tipo de suco. Por exemplo, foram pedidos 10 sucos exclusivamente de abacaxi e 6 sucos usando apenas laranja e morango.
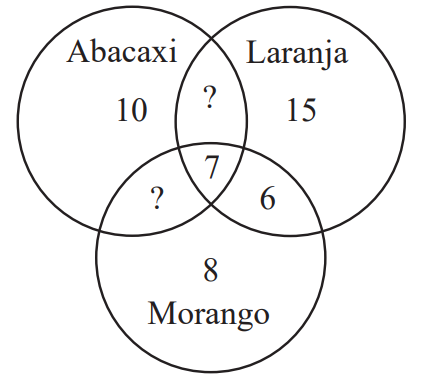
Os sucos foram colocados em copos não rotulados. Se uma pessoa escolher um copo ao acaso, qual a probabilidade de ela tomar um suco com exatamente dois sabores?
a) \( \frac{5}{13} \) b) \( \frac{1}{10} \) c) \( \frac{7}{22} \) d) \( \frac{2}{7} \)
1º Passo – Determinar os valores faltantes:
Total de copos: 65 Somando os valores do diagrama com incógnitas \( x \) e \( y \): \[ 10 + 15 + 8 + 7 + 6 + x + y = 65 \] \[ x + y = 19 \]
2º Passo – Quantidade de copos com exatamente dois sabores:
Os copos com exatamente dois sabores são: \[ x + y + 6 = 25 \]
3º Passo – Cálculo da probabilidade:
\[ P = \frac{25}{65} = \frac{5}{13} \]
Resposta Final: \[ \frac{5}{13} \quad \text{(Alternativa A)} \]
