Números Inteiros — Definição, Operações, Propriedades e Exercícios
Atualizado em 22 de agosto de 2025 • Leitura: ~13 min • Conteúdo com teoria, exemplos e exercícios
O que são Números Inteiros?
Os números inteiros formam o conjunto \(\mathbb{Z}\), que inclui todos os números naturais, seus opostos e o zero:
Eles são fundamentais para representar ganhos e perdas, temperaturas, altitudes e qualquer situação que envolva valores positivos e negativos.
Conexão com Conjuntos Numéricos: os inteiros incluem os naturais, são subconjunto dos racionais, e participam da composição dos reais.
Representação na Reta Numérica
A reta numérica é usada para visualizar a posição dos inteiros:
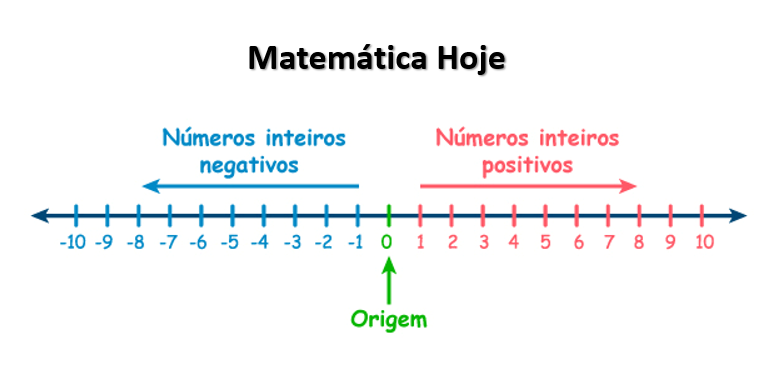
- À direita de 0 → valores positivos.
- À esquerda de 0 → valores negativos.
- O 0 é o elemento neutro aditivo.
Operações com Números Inteiros
Adição
Mesmos sinais: soma-se os módulos e mantém o sinal.
Sinais diferentes: subtrai-se os módulos e mantém o sinal do maior.
Subtração
Transforma-se a subtração em adição: \(a-b = a+(-b)\).
Multiplicação
- (+)×(+) = positivo
- (-)×(-) = positivo
- (+)×(-) = negativo
Divisão
- Regra de sinais igual à da multiplicação.
- Divisão por zero é indefinida.
Módulo e Distância
O módulo de um número inteiro representa sua distância até o zero na reta numérica:
Exemplo: \(|-7|=7\), \(|5|=5\).
Exemplos Resolvidos
Exemplo 1 — Operações com sinais
Enunciado: Calcule: \((-8) + 13 – (-5)\).
Solução passo a passo
- \((-8)+13=5\).
- \(5 – (-5)=5+5=10\).
- Resposta: \(10\).
Exemplo 2 — Módulo e distância
Enunciado: Qual a distância entre \(-4\) e \(7\)?
Solução passo a passo
- Distância = \(|(-4)-7|=|-11|=11\).
- Resposta: \(11\) unidades.
Exercícios Propostos
- Resolva: \((-7)+15-8\)
- Calcule: \((-4)\cdot 6\)
- Determine: \(|-12| + |5|\)
- Resolva: \((-18)\div(-3)\)
- Qual a distância entre \(3\) e \(-10\)?
Gabarito (clique para ver)
1) 0 • 2) -24 • 3) 17 • 4) 6 • 5) 13
Erros Comuns e Dicas
- Confundir regras de sinais na multiplicação e divisão.
- Esquecer que subtração é adição do oposto.
- Ignorar que distância entre pontos usa módulo.
Leituras Relacionadas
Resumo e Materiais para Estudo
- ✔ Definição de \(\mathbb{Z}\)
- ✔ Operações básicas com sinais
- ✔ Uso do módulo e distância
- ✔ Exemplos resolvidos e exercícios













