Área do Trapézio
Chamamos de trapézio o quadrilátero que possui um par de lados paralelos (bases): base maior \(B\) e base menor \(b\). A altura \(h\) é a distância perpendicular entre as bases. Nosso foco é calcular a área do trapézio em diferentes situações.
Como a mediana (segmento médio) é \(m=\dfrac{B+b}{2}\), também vale \(\;A=m\cdot h\).
Reconhecendo os tipos (para achar a altura)
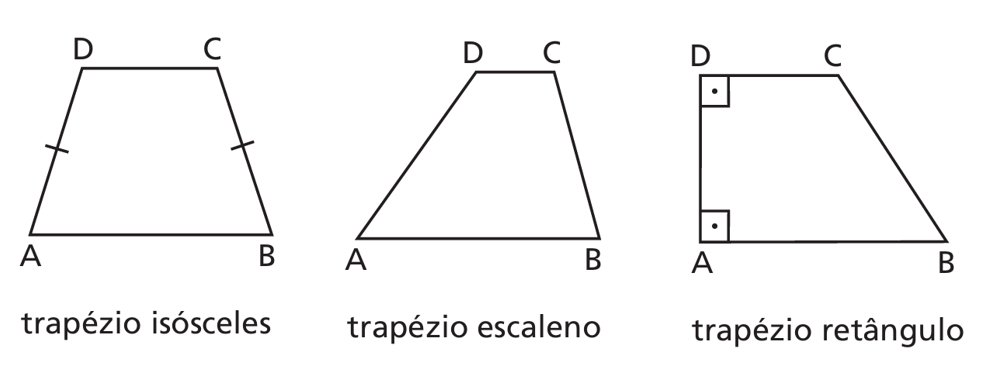
Escaleno: sem igualdades; a altura costuma vir por projeção/semelhança ou decomposição em triângulos.
Isósceles: pernas congruentes; pode-se usar \(h=\sqrt{\ell^2-\left(\dfrac{B-b}{2}\right)^2}\).
Como chegar à fórmula da área
Divida o trapézio em dois triângulos pela diagonal e some as áreas: \(A=\dfrac{1}{2}B\cdot h+\dfrac{1}{2}b\cdot h=\dfrac{(B+b)h}{2}\).
Alternativa geral (qualquer quadrilátero convexo): \(A=\dfrac{1}{2}d_1d_2\sin\theta\), onde \(d_1\) e \(d_2\) são diagonais e \(\theta\) o ângulo entre elas.
Exemplos resolvidos (situação-problema)
Área direta com altura
- Cenário
- Piso de um mezanino.
- Dados
- \(B=8\,\text{m}\), \(b=5\,\text{m}\), \(h=3\,\text{m}\).
Pergunta: qual é a área do trapézio para o piso?
Ver solução
Trapézio retângulo (altura é a lateral)
- Cenário
- Placa metálica.
- Dados
- \(B=14\,\text{cm}\), \(b=6\,\text{cm}\), \(h=4\,\text{cm}\).
Pergunta: encontre a área do trapézio.
Ver solução
Trapézio isósceles (altura por Pitágoras)
- Cenário
- Vidro automotivo.
- Dados
- \(B=30\,\text{cm}\), \(b=18\,\text{cm}\), \(\ell=10\,\text{cm}\) (pernas iguais).
Pergunta: qual é a área do trapézio?
Ver solução
Usando diagonais e ângulo
- Cenário
- Terreno irregular.
- Dados
- \(d_1=26\,\text{m}\), \(d_2=18\,\text{m}\), \(\theta=40^\circ\).
Pergunta: calcule a área do trapézio.
Ver solução
Exercícios propostos (situação-problema)
Orçamento de jardim — área direta
- Cenário
- Um canteiro tem forma de trapézio.
- Dados
- Bases \(B=20\,\text{cm}\) e \(b=9\,\text{cm}\); altura \(h=7\,\text{cm}\).
Pergunta: qual é a área do trapézio para estimar a terra?
Vitral isósceles — descubra a altura e a área
- Cenário
- Um vitral tem moldura em trapézio isósceles.
- Dados
- Base maior \(B=36\,\text{cm}\), base menor \(b=22\,\text{cm}\), pernas iguais \(\ell=13\,\text{cm}\).
Pergunta: calcule a altura \(h\) e, em seguida, a área do trapézio.
Plataforma retângulo-inclinada — lateral é a altura
- Cenário
- Uma plataforma em trapézio retângulo servirá de base para um tanque.
- Dados
- Base maior \(B=15\,\text{m}\), base menor \(b=11\,\text{m}\), lateral perpendicular \(h=4{,}5\,\text{m}\).
Pergunta: determine a área do trapézio para dimensionar a chapa.
Levantamento de terreno — diagonais e ângulo
- Cenário
- O lote tem forma aproximada de trapézio.
- Dados
- Diagonais \(d_1=30\,\text{m}\) e \(d_2=25\,\text{m}\); ângulo entre elas \(\theta=55^\circ\).
Pergunta: usando \(A=\tfrac12 d_1 d_2 \sin\theta\), qual é a área do trapézio?
Continue estudando (linkagem interna)
Área de Triângulo — base–altura, 2 lados + ângulo, Heron.
Lei dos Senos e Lei dos Cossenos — úteis ao decompor o trapézio em triângulos.
Triângulos: tipos e propriedades — para revisar projeções e semelhança.
Materiais do Matemática Hoje
Lista de exercícios — múltipla escolha (situação-problema)
Mezanino — área direta
- Cenário
- Um piso de mezanino tem forma trapezoidal.
- Dados
- Bases \(B=12\,\text{cm}\), \(b=8\,\text{cm}\); altura \(h=5\,\text{cm}\).
Pergunta: qual é a área do trapézio?
- A) \(40\text{ cm}^2\)
- B) \(45\text{ cm}^2\)
- C) \(50\text{ cm}^2\)
- D) \(60\text{ cm}^2\)
Gabarito e solução
Painel — encontre a altura
- Cenário
- Um painel trapezoidal será fixado numa parede.
- Dados
- Área \(A=96\,\text{m}^2\), bases \(B=14\,\text{m}\), \(b=10\,\text{m}\).
Pergunta: qual deve ser a altura \(h\)?
- A) \(6\,\text{m}\)
- B) \(7\,\text{m}\)
- C) \(8\,\text{m}\)
- D) \(9\,\text{m}\)
Gabarito e solução
Vidro automotivo (isósceles)
- Cenário
- Um vidro de carro tem moldura em trapézio isósceles.
- Dados
- Bases \(B=30\,\text{cm}\), \(b=18\,\text{cm}\); pernas \(\ell=10\,\text{cm}\).
Pergunta: qual é a área do trapézio?
- A) \(180\ \text{cm}^2\)
- B) \(192\ \text{cm}^2\)
- C) \(200\ \text{cm}^2\)
- D) \(210\ \text{cm}^2\)
Gabarito e solução
Plataforma retângula
- Cenário
- Base de uma plataforma em trapézio retângulo.
- Dados
- Bases \(B=15\,\text{m}\), \(b=9\,\text{m}\); altura \(h=4{,}5\,\text{m}\).
Pergunta: qual é a área?
- A) \(48\ \text{m}^2\)
- B) \(52{,}5\ \text{m}^2\)
- C) \(54\ \text{m}^2\)
- D) \(56\ \text{m}^2\)
Gabarito e solução
Terreno — diagonais e ângulo
- Cenário
- Levantamento de um lote trapezoidal.
- Dados
- Diagonais \(d_1=26\,\text{m}\), \(d_2=18\,\text{m}\); ângulo \(\theta=40^\circ\).
Pergunta: qual é a área?
- A) \(146{,}0\ \text{m}^2\)
- B) \(150{,}3\ \text{m}^2\)
- C) \(150{,}4\ \text{m}^2\)
- D) \(154{,}0\ \text{m}^2\)
Gabarito e solução
Piso técnico — mediana
- Cenário
- Piso elevado em módulos trapezoidais.
- Dados
- Mediana \(m=11\,\text{cm}\), altura \(h=7\,\text{cm}\).
Pergunta: qual é a área?
- A) \(72\ \text{cm}^2\)
- B) \(77\ \text{cm}^2\)
- C) \(84\ \text{cm}^2\)
- D) \(88\ \text{cm}^2\)
Gabarito e solução
Outdoor — base menor desconhecida
- Cenário
- Impressão de lona trapezoidal.
- Dados
- Área \(A=63\,\text{m}^2\), altura \(h=7\,\text{m}\), base maior \(B=11\,\text{m}\).
Pergunta: qual é a base menor \(b\)?
- A) \(5\,\text{m}\)
- B) \(6\,\text{m}\)
- C) \(7\,\text{m}\)
- D) \(9\,\text{m}\)
Gabarito e solução
Qual par NÃO serve?
- Cenário
- Dimensionamento rápido de peças.
- Dados
- \(A=48\,\text{m}^2\), \(h=6\,\text{m}\).
Pergunta: qual par de bases não é possível?
- A) \(B=10\,\text{m},\ b=6\,\text{m}\)
- B) \(B=12\,\text{m},\ b=3\,\text{m}\)
- C) \(B=9\,\text{m},\ b=7\,\text{m}\)
- D) \(B=13\,\text{m},\ b=3\,\text{m}\)
Gabarito e solução
Variação percentual
- Cenário
- Projeto mantém as bases; altera-se a altura.
- Dados
- Altura aumenta \(15\%\) e \(B,b\) constantes.
Pergunta: de quanto varia a área?
- A) \(+7{,}5\%\)
- B) \(+15\%\)
- C) \(+30\%\)
- D) Depende
Gabarito e solução
Conversão de unidades
- Cenário
- Placa técnica com medidas mistas.
- Dados
- \(B=1{,}2\,\text{m}\), \(b=80\,\text{cm}\), \(h=50\,\text{cm}\).
Pergunta: qual é a área em \(\text{m}^2\)?
- A) \(0{,}25\ \text{m}^2\)
- B) \(0{,}5\ \text{m}^2\)
- C) \(0{,}05\ \text{m}^2\)
- D) \(5\ \text{m}^2\)
Gabarito e solução
Altura em trapézio isósceles
- Cenário
- Moldura isósceles precisa da altura para corte.
- Dados
- \(B=22\,\text{cm}\), \(b=10\,\text{cm}\), \(\ell=8\,\text{cm}\).
Pergunta: qual é a altura \(h\)?
- A) \(4{,}00\ \text{cm}\)
- B) \(5{,}29\ \text{cm}\)
- C) \(6{,}00\ \text{cm}\)
- D) \(7{,}00\ \text{cm}\)
Gabarito e solução
Conceito — marque a correta
- Cenário
- Revisão conceitual para prova.
- Dados
- Definições de altura, mediana e propriedades.
Pergunta: sobre trapézios, assinale a alternativa verdadeira.
- A) A altura é qualquer lado inclinado.
- B) A mediana é a média aritmética das bases.
- C) A área independe da altura.
- D) Em trapézio retângulo, as bases são perpendiculares.













