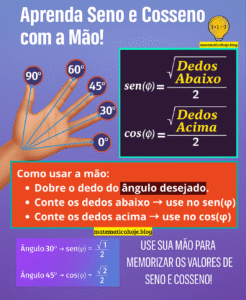
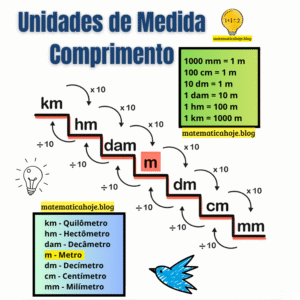
Classificação de Triângulo quanto aos Lados

O que significa classificar “quanto aos lados”?
Essa classificação considera apenas os comprimentos dos lados do triângulo. A soma dos ângulos internos é sempre \(180^\circ\), mas o tipo é definido pelo número de lados iguais.
Para a classificação por ângulos, veja: triângulo retângulo, triângulo acutângulo e triângulo obtusângulo. O guia geral está em Tipos de Triângulos.
Triângulo Equilátero — ΔABC
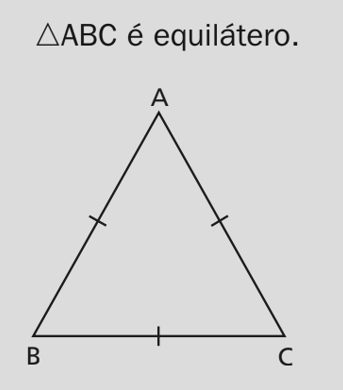
No equilátero, todas as medianas, alturas e bissetrizes coincidem. É o caso de ΔABC na imagem principal.
Revisão rápida? Veja os Mapas Mentais de Matemática.
Triângulo Isósceles — ΔRST
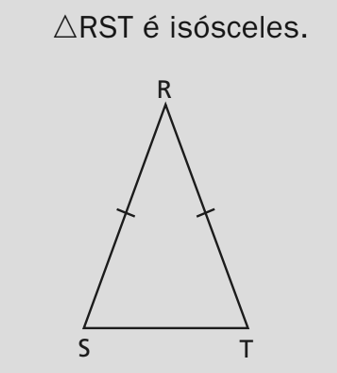
No isósceles, a altura até a base coincide com a mediana e com a bissetriz do ângulo do vértice (em ΔRST, o ângulo em R).
Triângulo Escaleno — ΔMNP
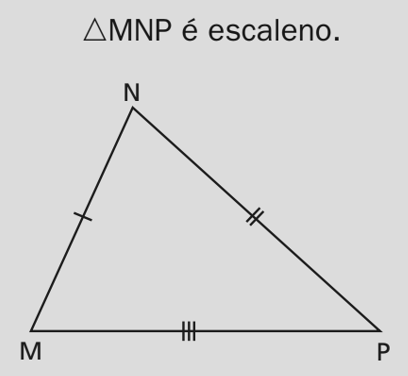
No escaleno (como ΔMNP), não há simetrias especiais. Vale a ordem: maior lado ↔ maior ângulo oposto.
Para aprofundar áreas e alturas: Área de Triângulo e Pontos Notáveis.
Exemplos resolvidos (contas empilhadas)
Exemplo 1 — Classifique o triângulo de lados \(8,8,5\).
Mostrar solução
Dois lados iguais \((8=8)\) ⇒ isósceles (como ΔRST).
Verifique existência:
\(8 < 8+5\)
\(8 < 13\) ✓
\(8 < 8+5\)
\(8 < 13\) ✓
\(5 < 8+8\)
\(5 < 16\) ✓
Exemplo 2 — ΔABC é equilátero com lado \(a=10\). Calcule a altura e a área.
Mostrar solução
Altura:
\(h=\frac{\sqrt{3}}{2}\,a\)
\(=\frac{\sqrt{3}}{2}\cdot 10\)
\(=5\sqrt{3}\) (≈ \(8{,}66\))
Área:
\(A=\frac{\sqrt{3}}{4}\,a^2\)
\(=\frac{\sqrt{3}}{4}\cdot 100\)
\(=25\sqrt{3}\) (≈ \(43{,}30\))
Exemplo 3 — Verifique se \(7,10,18\) formam triângulo. Se sim, classifique.
Mostrar solução
Existência:
\(7 < 10+18 \Rightarrow 7<28\) ✓
\(10 < 7+18 \Rightarrow 10<25\) ✓
\(18 \stackrel{?}{<} 7+10\)
\(18 \stackrel{?}{<} 17\) ✗
Não satisfaz a desigualdade triangular ⇒ não forma triângulo.
Exercícios de múltipla escolha (com solução em abre/fecha)
1) Classifique os lados \(4,4,6\).
Mostrar solução
Dois lados iguais ⇒ isósceles. Verificação: \(6<4+4\Rightarrow 6<8\) ✓.
2) Um triângulo com lados \(9,9,9\) é:
Mostrar solução
Três lados iguais ⇒ equilátero (como ΔABC).
3) Lados \(5,6,7\) formam que tipo?
Mostrar solução
Todos diferentes ⇒ escaleno (como ΔMNP). E existe: \(7<11\), \(6<12\), \(5<13\).
4) Para ser equilátero com perímetro \(P=24\), cada lado mede:
Mostrar solução
\(a=\dfrac{P}{3}\)
\(=\dfrac{24}{3}\)
\(=8\).
5) Qual das seguintes não forma triângulo?
Mostrar solução
Teste a maior medida: deve ser < soma das outras duas.
Em E: \(5 \not< 2+2\Rightarrow 5 \not< 4\) ⇒ não forma triângulo.
6) Em ΔRST (isósceles), a base mede \(12\) e a altura relativa à base mede \(5\). A área é:
Mostrar solução
\(A=\dfrac{b\cdot h}{2}\)
\(=\dfrac{12\cdot 5}{2}\)
\(=30\).
7) Em ΔABC (equilátero) de lado \(a\), a altura \(h\) vale:
Mostrar solução
Altura do equilátero: \(h=\dfrac{\sqrt{3}}{2}a\).
8) Se um triângulo tem dois lados \(x\) e \(x\) e o terceiro \(y\) com \(y=2x\), então:
Mostrar solução
\(y<x+x \Rightarrow 2x<2x\) (falso) ⇒ não forma triângulo.
9) Em ΔRST (isósceles) com lados iguais \(10\) e base \(12\), a altura é:
Mostrar solução
Altura divide a base: semilado \(=6\).
\(h^2+6^2=10^2\)
\(h^2+36=100\)
\(h^2=64\Rightarrow h=8\).
10) Qual é a área de ΔABC (equilátero) de lado \(12\)?
Mostrar solução
\(A=\dfrac{\sqrt{3}}{4}a^2\)
\(=\dfrac{\sqrt{3}}{4}\cdot 144\)
\(=36\sqrt{3}\).
Continue estudando
Triângulo equilátero (ΔABC) Triângulo isósceles (ΔRST) Triângulo escaleno (ΔMNP) Área de triângulo Pontos notáveis Tipos de triângulos Triângulo retângulo Triângulo acutângulo Triângulo obtusângulo
Materiais recomendados
Mapas Mentais de Matemática
Resumos visuais com as fórmulas de ΔABC, ΔRST e ΔMNP.
Quero os Mapas+600 Questões ENEM Matemática
Pratique classificação por lados e por ângulos com gabarito.
Praticar agoraColeção 10 eBooks
Teoria direta + listas resolvidas de Geometria Plana.
Ver coleçãoBanco de Questões
Monte listas por assunto com nível e gabarito.
Acessar bancoCanais Oficiais
Receba avisos de novos artigos, simulados e materiais.
Entrar nos canais