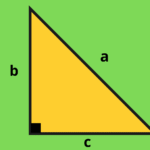
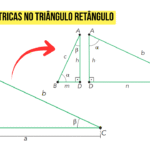
Triângulo Agudo (Acutângulo)
SEO discreto: usamos naturalmente “triângulo agudo” e “triângulo acutângulo”.
Definição e reconhecimento
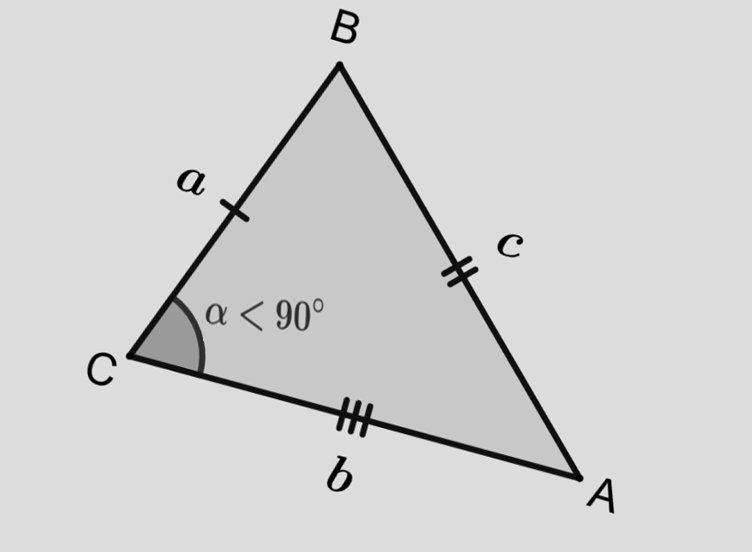
Um triângulo agudo é aquele em que todos os ângulos internos são menores que \(90^\circ\): \( \angle A<90^\circ,\ \angle B<90^\circ,\ \angle C<90^\circ \).
Dica rápida: o maior ângulo fica oposto ao maior lado. Em triângulos agudos, esse maior ângulo segue sendo menor que \(90^\circ\).
Propriedades importantes
- Pontos notáveis (ortocentro, baricentro, incentro e circuncentro) ficam dentro do triângulo. Veja Pontos Notáveis.
- As alturas são segmentos internos (no obtusângulo, algumas ficam externas).
- A classificação por lados é independente: um triângulo agudo pode ser equilátero, isósceles ou escaleno.
Fórmulas essenciais (uma por linha)
Para comparar com outras classes por ângulo: triângulo retângulo e triângulo obtusângulo. Veja também o panorama em Tipos de Triângulos.
Exemplos resolvidos (passo a passo vertical)
Exemplo 1 — Classifique o triângulo de lados \(7,8,9\).
Mostrar solução
Maior lado: \(c=9\).
\(c^2=9^2\)
=81
\(a^2+b^2=7^2+8^2\)
=49+64
=113
Como \(81<113\), o triângulo é agudo.
Exemplo 2 — \(a=10\), \(b=11\), \(C=60^\circ\). Calcule \(c\) e classifique.
Mostrar solução
\(c^2=a^2+b^2-2ab\cos C\)
\(=10^2+11^2-2\cdot10\cdot11\cdot\frac12\)
\(=221-110\)
\(=111\)
\(c=\sqrt{111}\approx 10{,}54\). Como \(C=60^\circ<90^\circ\), é agudo.
Exemplo 3 — Ângulos \(65^\circ\), \(70^\circ\) e \(45^\circ\). Classifique.
Mostrar solução
Todas as medidas < \(90^\circ\) ⇒ triângulo agudo.
Reforce: Área de Triângulo.
Exercícios de múltipla escolha (com solução em abre/fecha)
1) Classifique o triângulo de lados \(5,6,8\).
Mostrar solução
Maior lado \(c=8\).
\(c^2=8^2\)
=64
\(a^2+b^2=5^2+6^2\)
=25+36
=61
Como \(64>61\), é obtusângulo. Alternativa B.
2) Quais ângulos caracterizam um triângulo agudo?
Mostrar solução
Definição direta. Alternativa C.
3) Dadas \(a=7\), \(b=9\), \(c=10\), classifique.
Mostrar solução
Maior lado \(c=10\).
\(c^2=10^2\)
=100
\(a^2+b^2=7^2+9^2\)
=49+81
=130
Como \(100<130\), é agudo. Alternativa A.
4) Se \(C=70^\circ\) e \(a=8\), \(b=11\), então o triângulo é:
Mostrar solução
Lei dos cossenos:
\(c^2=8^2+11^2-2\cdot 8\cdot 11\cos70^\circ\)
\(\approx 185-176\cdot 0{,}3420\)
\(\approx 124{,}808\Rightarrow c\approx 11{,}17\)
\(\cos A\approx\dfrac{121+124{,}808-64}{2\cdot 11\cdot 11{,}17}\approx 0{,}740\Rightarrow A\approx 42{,}3^\circ\)
Logo \(B\approx 67{,}7^\circ\). Todos < \(90^\circ\) ⇒ agudo. Alternativa A.
5) Para que \(7,9,c\) (com \(c\) maior) forme triângulo agudo, é necessário:
Mostrar solução
Agudo ⇔ \(c^2<7^2+9^2=130\) e \(c>9\). Logo 9<c<\sqrt{130}\approx 11{,}40. Alternativa C.
6) Um triângulo tem ângulos \(x, y, z\) com \(x=2y\) e \(z=70^\circ\). Para ser agudo, \(y\) deve satisfazer:
Mostrar solução
\(2y+y+70=180\)
\(3y=110\)
\(y=\dfrac{110}{3}\approx 36{,}67^\circ\)
Os outros dois: \(73{,}33^\circ\) e \(70^\circ\) (todos agudos). Correta: C.
7) Em triângulo agudo, o ortocentro está:
Mostrar solução
No agudo, ortocentro, circuncentro e incentro são internos. Alternativa B.
8) Se \(a=12\), \(b=13\) e o triângulo é agudo em \(C\), então \(\sin C\) é:
Mostrar solução
Ângulo agudo tem seno entre 0 e 1 (exclusivo). Alternativa C.
9) Um triângulo tem \(a=8\), \(b=15\), \(c=17\). Classifique.
Mostrar solução
\(c^2=17^2=289\)
\(a^2+b^2=8^2+15^2=64+225=289\)
Igualdade de Pitágoras ⇒ retângulo. Alternativa B.
10) Num triângulo agudo com \(a=9\), \(b=12\) e \(C=60^\circ\), a área é:
Mostrar solução
\(A=\dfrac{ab\sin C}{2}\)
\(=\dfrac{9\cdot 12\cdot \sin 60^\circ}{2}\)
\(=\dfrac{108\cdot \frac{\sqrt3}{2}}{2}\)
\(=\dfrac{108\sqrt3}{4}\)
\(=27\sqrt3\).
Alternativa C.
Continue estudando
Triângulo acutângulo Triângulo retângulo Triângulo obtusângulo Triângulo equilátero Triângulo isósceles Triângulo escaleno Área de triângulo Pontos notáveis Tipos de triângulos
Materiais recomendados
Mapas Mentais de Matemática
Critérios para triângulos agudos, retângulos e obtusos em uma página.
Quero os Mapas+600 Questões ENEM Matemática
Triângulos, áreas, semelhança e trigonometria com gabarito comentado.
Praticar agoraColeção 10 eBooks
Teoria direta + listas resolvidas de Geometria Plana.
Ver coleçãoBanco de Questões
Monte listas por assunto e nível — perfeito para fixar triângulos agudos.
Acessar bancoCanais Oficiais
Receba avisos de novos artigos, simulados e materiais.
Entrar nos canais