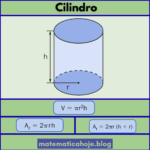
Área do Cilindro
O cilindro circular reto aparece em latas, copos, tubos e tanques. Aqui você encontra as fórmulas de área lateral, área das bases e área total, com demonstração por planificação, exemplos e exercícios.
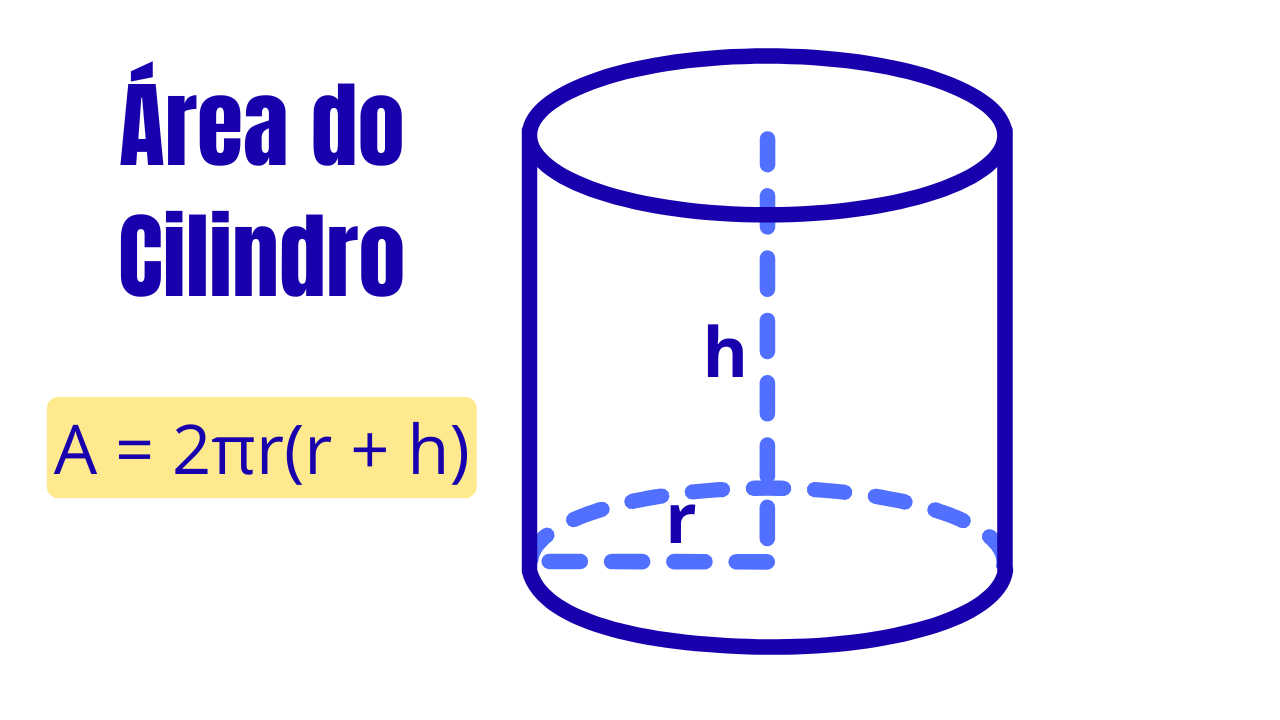
Notação usada no artigo: \(r\) é o raio do círculo da base. \(h\) é a altura (distância perpendicular entre os planos das bases). Sempre que falarmos em “cilindro” estamos nos referindo ao cilindro reto, salvo aviso em contrário.
Para revisar o sólido completo (elementos, propriedades e volume), veja Cilindro e Fórmula Volume do Cilindro. Contexto geral em Corpos redondos (compare com cone e esfera).
Fórmulas de área
Área lateral (rótulo/“casca”): \(\displaystyle A_L=2\pi r h\)
Área de uma base (círculo): \(\displaystyle A_{\text{base}}=\pi r^2\)
Área total (duas bases + lateral):
\(\displaystyle A_T=2\pi r h+2\pi r^2=2\pi r(r+h)\)
Unidades: se \(r\) e \(h\) estão em cm, a área sai em cm². Em aplicações práticas (pintura, materiais), confira se o problema inclui ou exclui tampas.
Por que as fórmulas funcionam? (planificação)
Ao “abrir” a superfície do cilindro, obtemos um retângulo (a superfície lateral) e dois círculos (as bases):
- O retângulo tem largura igual à circunferência da base \(2\pi r\) e altura \(h\) ⇒ área \(A_L=2\pi r\cdot h\).
- Cada base é um círculo de área \(\pi r^2\); como são duas, \(2\pi r^2\).
Somando: \(A_T=A_L+2\pi r^2=2\pi r h+2\pi r^2=2\pi r(r+h)\).
Variações frequentes
- Cilindro sem tampa (aberto em cima): \(A = A_L + A_{\text{base}} = 2\pi r h + \pi r^2\).
- Cilindro sem fundo (aberto embaixo): \(A = A_L + \pi r^2\).
- Apenas rótulo (sem tampas): \(A = A_L = 2\pi r h\).
- Tubo cilíndrico oco, sem tampas, com espessura desprezível: áreas expostas = lateral externa \(2\pi R h\) + lateral interna \(2\pi r h\) + duas coroas nas extremidades \(2\pi(R^2-r^2)\). Assim, \(\displaystyle A_{\text{tubo}}=2\pi Rh+2\pi r h+2\pi(R^2-r^2)=2\pi\big[h(R+r)+(R^2-r^2)\big]\).
Exemplos resolvidos
Exemplo 1 – Lata com tampa e fundo. \(r=4\) cm e \(h=10\) cm. Calcule a área total.
Ver solução
\(A_T=2\pi r(r+h)=2\pi\cdot4\cdot(4+10)=112\pi\approx \mathbf{351{,}86\ \text{cm}^2}\).
Exemplo 2 – Só o rótulo (planificação conhecida). O rótulo tem 25 cm de largura (circunferência) e 20 cm de altura. Determine a área lateral e a área total.
Ver solução
Como \(2\pi r=25\Rightarrow r=25/(2\pi)\approx 3{,}979\) cm. \(A_L=(2\pi r)\cdot h=25\cdot20=\mathbf{500\ \text{cm}^2}\). \(A_T=A_L+2\pi r^2=500+25\cdot r\approx 500+99{,}47=\mathbf{599{,}47\ \text{cm}^2}\).
Exemplo 3 – Pote sem tampa. \(r=5\) cm e \(h=8\) cm. Calcule a área a ser pintada internamente.
Ver solução
\(A=2\pi r h+\pi r^2=2\pi\cdot5\cdot8+25\pi=105\pi\approx \mathbf{329{,}87\ \text{cm}^2}\).
Exemplo 4 – Tubo oco, sem tampas. \(R=6\) cm, \(r=5\) cm, \(h=10\) cm. Encontre a área exposta.
Ver solução
\(A=2\pi Rh+2\pi r h+2\pi(R^2-r^2)=2\pi(60+50+11)=242\pi\approx \mathbf{760{,}32\ \text{cm}^2}\).
Exercícios (múltipla escolha, com solução)
Em todos: \(r\) = raio da base; \(h\) = altura. Use \(\pi\approx3{,}1416\).
1) Cilindro reto com \(r=3\) cm e \(h=12\) cm. A área lateral e a total valem, respectivamente (em cm²): A) \(72\pi\) e \(90\pi\) B) \(60\pi\) e \(90\pi\) C) \(72\pi\) e \(84\pi\) D) \(60\pi\) e \(84\pi\)
Solução
\(A_L=2\pi rh=72\pi\). \(A_T=2\pi r(r+h)=2\pi\cdot3\cdot15=90\pi\). Alternativa A.
2) Um pote sem tampa tem \(r=4\) cm e \(h=10\) cm. A área a revestir internamente é (em cm²): A) \(96\pi\) B) \(100\pi\) C) \(112\pi\) D) \(120\pi\)
Solução
\(A=2\pi rh+\pi r^2=80\pi+16\pi=96\pi\). Alternativa A (≈ 301,59).
3) Um rótulo retangular de 22 cm (largura = circunferência da base) por 12 cm (altura) cobre a lateral da lata. A área do rótulo é: A) 220 B) 242 C) 264 D) 286 (cm²)
Solução
Área do rótulo = \(2\pi r\cdot h = 22\cdot 12=\mathbf{264}\). Alternativa C.
4) Se a área lateral é \(400\pi\) cm² e \(h=10\) cm, então o raio \(r\) é: A) 10 cm B) 15 cm C) 20 cm D) 25 cm
Solução
\(2\pi r h=400\pi\Rightarrow r=\frac{400}{2\cdot10}= \mathbf{20\ \text{cm}}\). Alternativa C.
5) Uma lata tem circunferência da base 25 cm e altura 20 cm. A área total aproximada é (em cm²): A) 595,0 B) 599,5 C) 605,0 D) 612,0
Solução
\(2\pi r=25\Rightarrow r=25/(2\pi)\). \(A_T=2\pi r(r+h)=(2\pi r)(r+h)=25(20+r)\approx \mathbf{599{,}47}\). Alternativa B.
6) Um tubo oco sem tampas tem \(R=6\) cm, \(r=5\) cm e \(h=10\) cm. A área exposta é (em cm²): A) \(200\pi\) B) \(220\pi\) C) \(242\pi\) D) \(260\pi\)
Solução
\(A=2\pi Rh+2\pi rh+2\pi(R^2-r^2)=242\pi\). Alternativa C (≈ 760,32).
7) Um tanque será pintado por fora, com tampa e sem fundo. Dados \(r=1{,}2\) m e \(h=2{,}5\) m, a área a pintar (m²) é: A) 20,42 B) 22,19 C) 23,36 D) 25,10
Solução
Externa: \(A=2\pi rh+\pi r^2=2\pi\cdot1{,}2\cdot2{,}5+\pi\cdot1{,}2^2=6\pi+1{,}44\pi=7{,}44\pi\approx \mathbf{23{,}36}\). Alternativa C.
8) Para volume fixo a área total mínima de uma lata ocorre quando \(h=2r\). Para \(V=1000\) cm³, qual par mais próximo dessa relação? A) \(r=5{,}0\) cm; \(h=10{,}0\) cm B) \(r=5{,}4\) cm; \(h=10{,}8\) cm C) \(r=6{,}0\) cm; \(h=12{,}0\) cm D) \(r=7{,}0\) cm; \(h=14{,}0\) cm
Solução
Se \(h=2r\), então \(V=\pi r^2(2r)=2\pi r^3=1000\Rightarrow r=(1000/2\pi)^{1/3}\approx 5{,}42\) cm, \(h\approx 10{,}84\) cm. Alternativa B.
9) Dadas \(r=4\) cm e área total \(A_T=112\pi\) cm², qual é a altura \(h\)? A) 8 B) 9 C) 10 D) 12
Solução
\(A_T=2\pi r(r+h)\Rightarrow 112\pi=2\pi\cdot4(r+h)\Rightarrow14=r+h\Rightarrow h=\mathbf{10}\). Alternativa C.
10) O rótulo de uma lata tem área 450 cm² e altura 18 cm. Qual é o raio da base? A) 3,54 cm B) 3,82 cm C) 3,98 cm D) 4,25 cm
Solução
Área do rótulo = \(2\pi rh\). Logo \(2\pi r=\frac{450}{18}=25\Rightarrow r=25/(2\pi)\approx \mathbf{3{,}98}\) cm. Alternativa C.