Volume da Esfera

A esfera é um sólido de revolução e um dos principais corpos redondos. Todos os seus pontos estão à mesma distância do centro; essa distância é o raio \(r\). Para propriedades e área da superfície, veja também: Esfera.

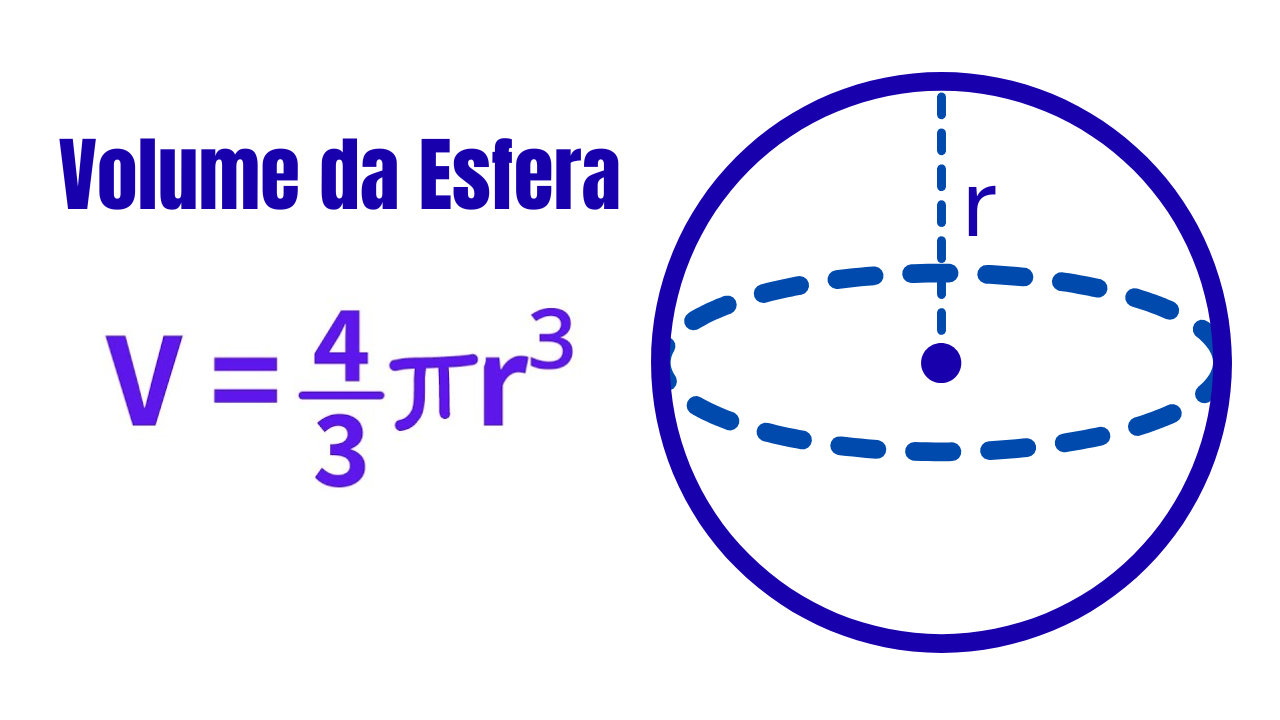
Fórmula do volume

\( V=\frac{4}{3}\,\pi\,r^{3} \)

\(V\) — volume da esfera;
\(\pi\approx3{,}14159\);
\(r\) — raio (mesmas unidades do resultado elevado ao cubo).

Exemplo resolvido

Calcule o volume de uma esfera de raio \(r=6\text{ cm}\).

\(V=\frac{4}{3}\pi r^{3}\)

\(V=\frac{4}{3}\pi \cdot 6^{3}\)

\(V=\frac{4}{3}\pi \cdot 216\)

\(V=288\pi\ \text{cm}^{3}\)

\(V\approx 904{,}32\ \text{cm}^{3}\)

Compare com outros sólidos

Exercícios (múltipla escolha)

1) Laboratório de química. Uma cápsula esférica de vidro tem raio de \(4\text{ cm}\). Qual é o volume interno?

A) \(\displaystyle \frac{256}{3}\pi\ \text{cm}^{3}\)
B) \(64\pi\ \text{cm}^{3}\)
C) \(85\pi\ \text{cm}^{3}\)
D) \(96\pi\ \text{cm}^{3}\)

Ver solução

\(V=\frac{4}{3}\pi r^{3}\)

\(V=\frac{4}{3}\pi\cdot 4^{3}\)

\(V=\frac{4}{3}\pi\cdot 64\)

\(V=\frac{256}{3}\pi\ \text{cm}^{3}\)

Resposta: A.

2) Esfera de decoração. Uma peça sólida tem volume \(288\pi\ \text{cm}^{3}\). Qual é o raio?

A) \(4\text{ cm}\)
B) \(5\text{ cm}\)
C) \(6\text{ cm}\)
D) \(8\text{ cm}\)

Ver solução

\( \frac{4}{3}\pi r^{3}=288\pi \)

\( r^{3}=\frac{3\cdot 288}{4}=216 \)

\( r=\sqrt[3]{216}=6\ \text{cm} \)

Resposta: C.

3) Bola de basquete. O diâmetro da bola é \(24\text{ cm}\). O volume aproximado é:

A) \(4\,188\ \text{cm}^{3}\)
B) \(6\,283\ \text{cm}^{3}\)
C) \(7\,238\ \text{cm}^{3}\)
D) \(9\,050\ \text{cm}^{3}\)

Ver solução

\(r=\frac{24}{2}=12\ \text{cm}\)

\(V=\frac{4}{3}\pi\cdot 12^{3}\)

\(V=\frac{4}{3}\pi\cdot 1728\)

\(V=2304\pi\ \text{cm}^{3}\)

\(V\approx 2304\cdot 3{,}1416=7\,238\ \text{cm}^{3}\)

Resposta: C.

4) Tanque esférico. Um reservatório esférico tem raio \(1{,}5\text{ m}\). Qual sua capacidade aproximada em litros?

A) \(9\,420\text{ L}\)
B) \(12\,000\text{ L}\)
C) \(14\,140\text{ L}\)
D) \(18\,850\text{ L}\)

Ver solução

\(V=\frac{4}{3}\pi\cdot 1{,}5^{3}\)

\(V=\frac{4}{3}\pi\cdot 3{,}375\)

\(V=4{,}5\pi\ \text{m}^{3}\)

\(V\approx 4{,}5\cdot 3{,}1416=14{,}137\ \text{m}^{3}\)

\(14{,}137\ \text{m}^{3}\approx 14\,137\ \text{L}\approx 14\,140\ \text{L}\)

Resposta: C.

5) Fundição. Uma esfera maciça de raio \(5\text{ cm}\) é derretida para produzir pequenas esferas de raio \(1\text{ cm}\). Quantas esferas menores são obtidas (sem perdas)?