Área de um Setor Circular
Setor circular é a “fatia” de pizza do círculo, delimitada por dois raios e um arco. Veja a fórmula, exemplos e exercícios.
1) Definição e elementos
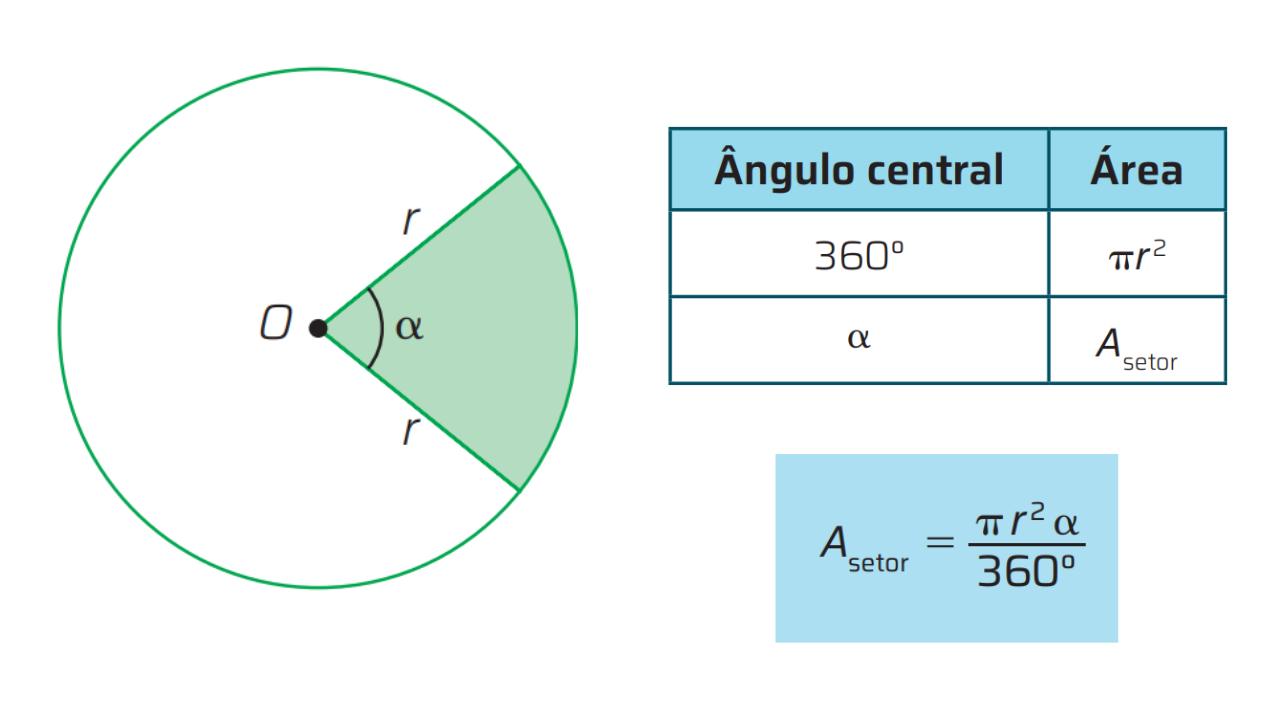
Um setor circular é a região do círculo limitada por dois raios \(r\) e por um arco central de ângulo \(\alpha\) (em graus). Quando \(\alpha=360^\circ\), o setor é o círculo inteiro; quando \(\alpha=180^\circ\), temos um semicírculo, e assim por diante.
2) Fórmula da área do setor
A área do setor é a fração da área do círculo proporcional ao ângulo central:
Se o ângulo estiver em radianos, use \(A_{\text{setor}}=\dfrac{1}{2}r^{2}\alpha\) (pois \(2\pi\) rad \(=360^\circ\)).
3) Exemplos resolvidos
Exemplo 1. Em um círculo de raio \(r=8\) cm, calcule a área do setor de \(\alpha=45^\circ\).
Mostrar solução
\(A=\dfrac{\pi\cdot8^2\cdot45}{360}=\dfrac{\pi\cdot64\cdot45}{360}=\dfrac{64}{8}\pi=8\pi\;\text{cm}^2\approx25{,}13\;\text{cm}^2\).
Exemplo 2. Um setor tem \(r=12\) cm e \(\alpha=\dfrac{\pi}{3}\) rad. Determine a área.
Mostrar solução
Com radianos: \(A=\dfrac{1}{2}r^2\alpha=\dfrac{1}{2}\cdot144\cdot\dfrac{\pi}{3}=24\pi\;\text{cm}^2\approx75{,}40\;\text{cm}^2\).
4) Relações úteis
Comprimento do arco correspondente ao setor (\(\alpha\) em graus):
Área em função do arco (com \(\alpha\) em radianos):
Como \(s=r\alpha\) (radianos), resulta \(A=\dfrac{1}{2}r^2\alpha\).
5) Exercícios (múltipla escolha)
1. Para \(r=10\) cm e \(\alpha=72^\circ\), a área do setor é:
- \(10\pi\)
- \(15\pi\)
- \(20\pi\)
- \(25\pi\)
Ver solução
\(A=\frac{\pi\cdot10^2\cdot72}{360}= \frac{100\pi}{5}=20\pi\;\text{cm}^2\). Alternativa C.
2. Um setor tem área \(A=12\pi\) cm² e \(r=6\) cm. Determine \(\alpha\) (graus).
- 60°
- 120°
- 150°
- 180°
Ver solução
\(12\pi=\frac{\pi\cdot6^2\cdot\alpha}{360}\Rightarrow 12\pi=\frac{36\pi\,\alpha}{360}\Rightarrow 12=\frac{\alpha}{10}\Rightarrow \alpha=120^\circ\). Alternativa B.
3. Em radianos, com \(r=5\) cm e \(\alpha=\dfrac{\pi}{4}\), a área é:
- \(\dfrac{5\pi}{4}\)
- \(\dfrac{25\pi}{8}\)
- \(\dfrac{25\pi}{8}\) cm²
- \(\dfrac{25}{8}\)
Ver solução
\(A=\frac{1}{2}r^2\alpha=\frac{1}{2}\cdot25\cdot\frac{\pi}{4}=\frac{25\pi}{8}\;\text{cm}^2\). Alternativa C.
6) Links para continuar estudando
Dica: pratique convertendo graus ↔ radianos: \( \alpha_{\text{rad}} = \alpha_{\text{graus}} \cdot \dfrac{\pi}{180} \).













