Matriz Quadrada: diagonal principal, diagonal secundária e matriz identidade
Neste guia reunimos, em um só lugar, tudo o que você precisa saber sobre matriz quadrada e suas diagonais, finalizando com a matriz identidade e exercícios resolvidos.
1) O que é uma matriz quadrada?
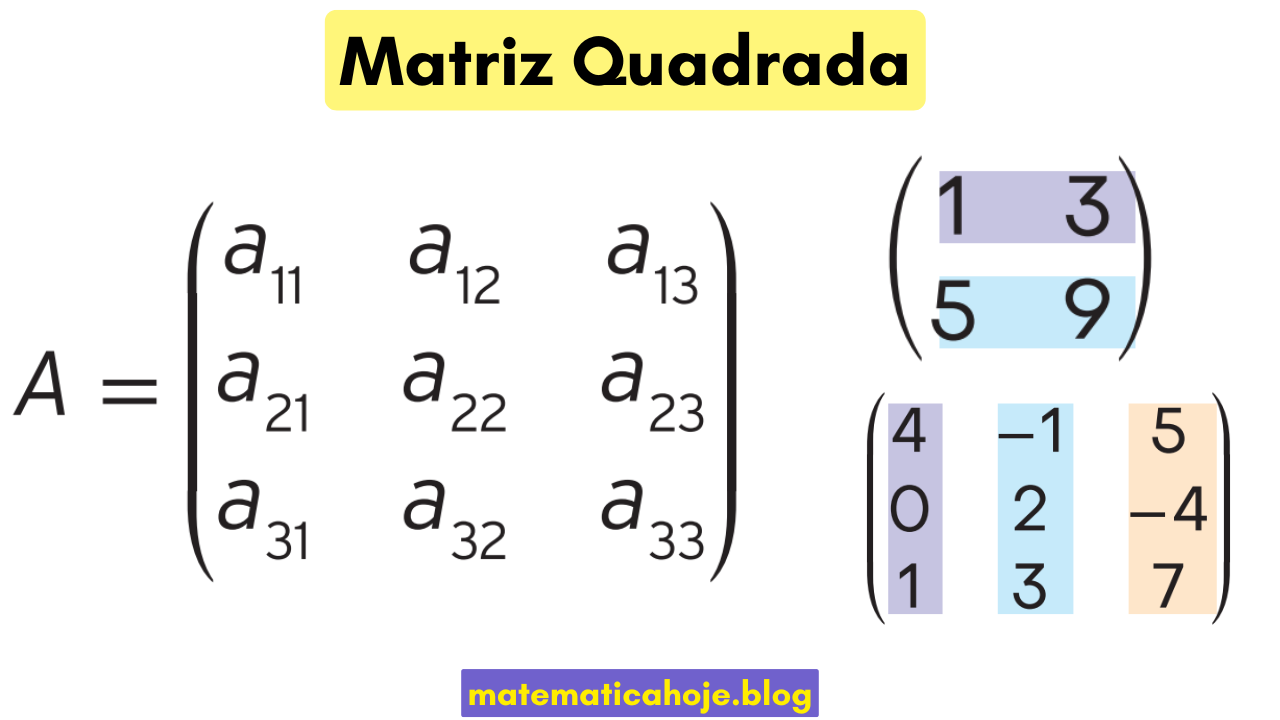
Uma matriz quadrada é uma matriz com o mesmo número de linhas e colunas, isto é, de ordem n×n. Em notação geral, escrevemos:
\( A = \big[a_{ij}\big]_{n\times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \)
Propriedades básicas
- Traço: \(\mathrm{tr}(A)=\sum_{i=1}^{n} a_{ii}\) (soma dos elementos da diagonal principal).
- Transposta: \(A^T\) é obtida trocando linhas por colunas.
- Simetria: \(A\) é simétrica se \(A=A^T\) e antissimétrica se \(A^T=-A\).
2) Diagonal principal
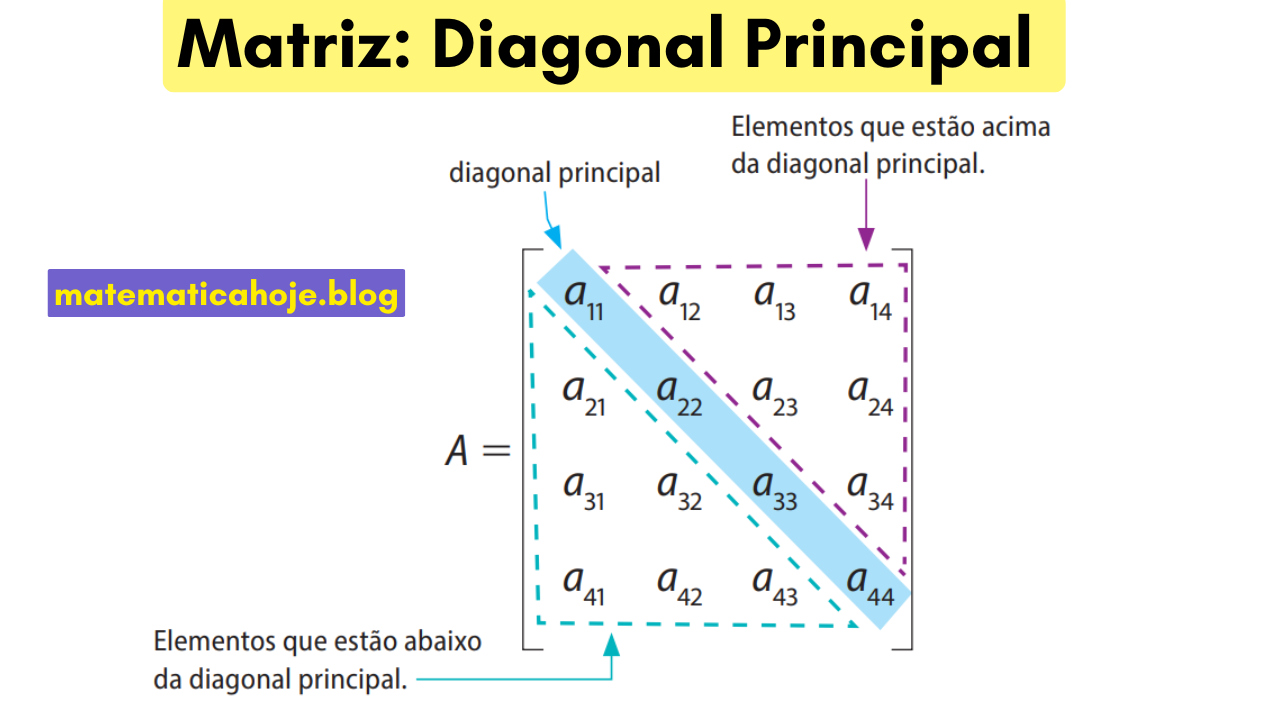
A diagonal principal de uma matriz quadrada \(A\) é o conjunto dos elementos cujos índices de linha e coluna coincidem: \(a_{11}, a_{22}, \ldots, a_{nn}\).
Acima e abaixo da diagonal
- Acima da diagonal principal: elementos com \(i < j\).
- Abaixo da diagonal principal: elementos com \(i > j\).
Exemplo
Para \( A=\begin{bmatrix} 4 & 1 & 2\\ 0 & -3 & 5\\ 7 & 6 & 9 \end{bmatrix}\), a diagonal principal é \( (4, -3, 9) \) e o traço é \(\mathrm{tr}(A)=4+(-3)+9=10\).
3) Diagonal secundária
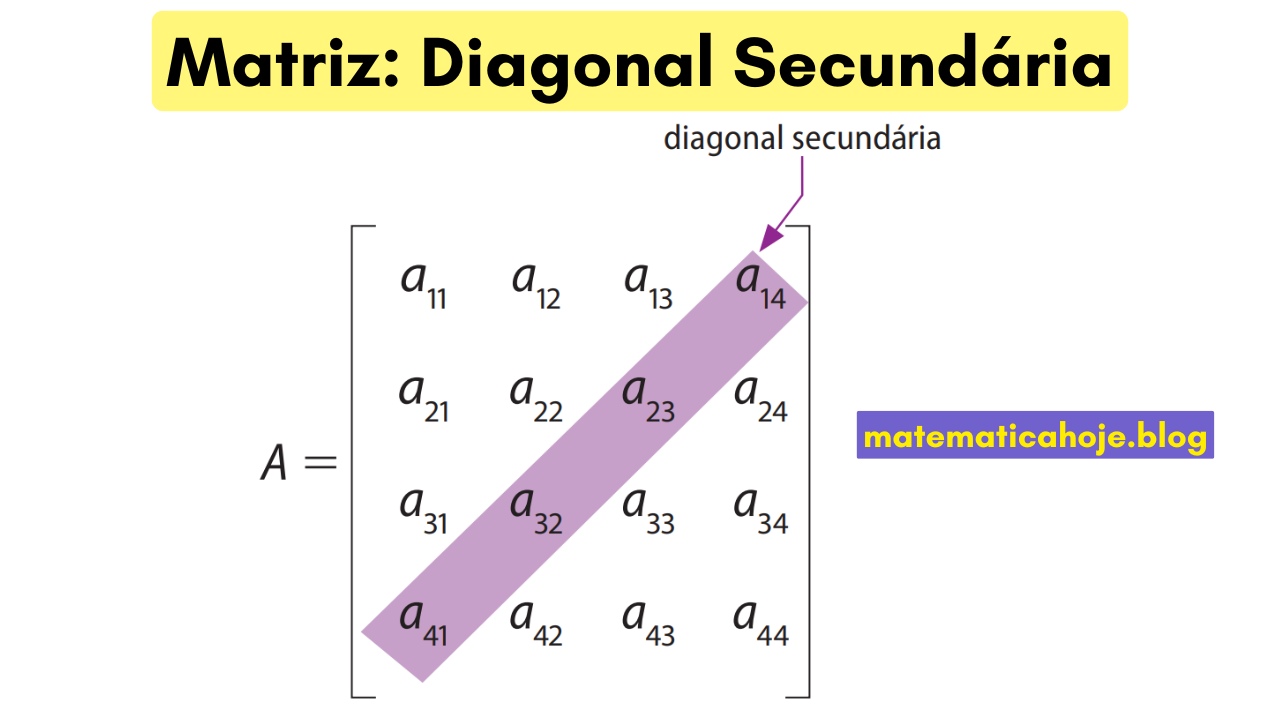
A diagonal secundária (ou anti-diagonal) reúne os elementos cuja soma dos índices é constante: \(i+j=n+1\). Para uma matriz 4×4, por exemplo, essa diagonal é \(a_{14}, a_{23}, a_{32}, a_{41}\).
Soma da diagonal secundária
Definimos \(s(A)=\sum_{i=1}^{n} a_{i,\,n+1-i}\). Para \( A=\begin{bmatrix} 4 & 1 & 2\\ 0 & -3 & 5\\ 7 & 6 & 9 \end{bmatrix} \) (3×3), a diagonal secundária é \( (2, -3, 7) \) e a soma é \(2+(-3)+7=6\).
4) Matriz identidade \(I_n\)
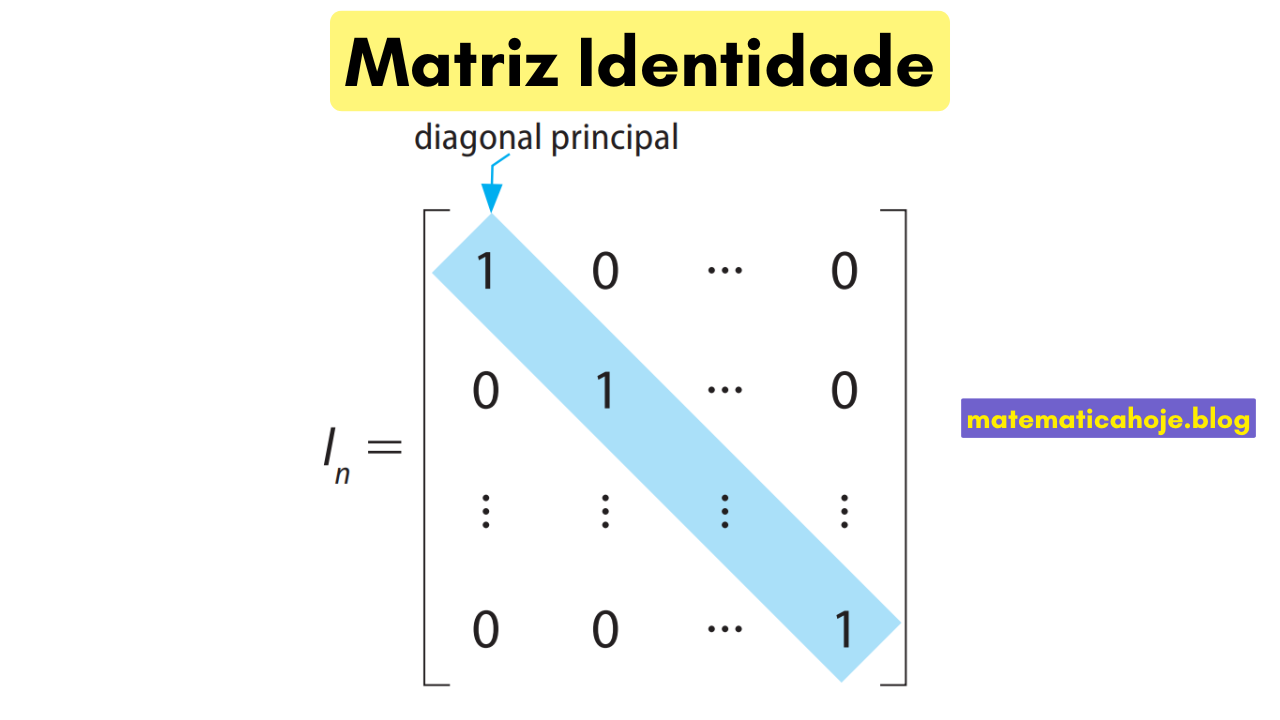
A matriz identidade de ordem \(n\), denotada por \(I_n\), é a matriz quadrada com 1 em todos os elementos da diagonal principal e 0 nos demais:
\( I_n=\begin{bmatrix} 1 & 0 & \cdots & 0\\ 0 & 1 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & 1 \end{bmatrix} \)
Propriedades essenciais
- Elemento neutro da multiplicação: \(I_n A = A I_n = A\) para toda \(A\) de ordem \(n\).
- Traço: \(\mathrm{tr}(I_n)=n\).
- Transposta: \(I_n^T=I_n\).
- Potência: \(I_n^k=I_n\) para todo inteiro \(k\ge 1\).
5) Exercícios de múltipla escolha
-
Considere \(A=\begin{bmatrix}2&-1&0\\ 4&3&5\\ 7&1&-2\end{bmatrix}\). A diagonal principal de \(A\) é:
- A) \((2,3,-2)\)
- B) \((0,3,7)\)
- C) \((0,5,-2)\)
- D) \((2,4,7)\)
Ver solução
Diagonal principal: \(a_{11},a_{22},a_{33}=(2,3,-2)\). Resposta: A.
-
Na mesma matriz \(A\), a diagonal secundária é:
- A) \((0,3,7)\)
- B) \((0,3,7)\) (ordem importa)
- C) \((0,3,7)\) com ordem correta: \((0,3,7)\)
- D) \((0,3,7)\) onde os termos são \(a_{13},a_{22},a_{31}\)
Ver solução
A diagonal secundária (3×3) é \(a_{13},a_{22},a_{31}=(0,3,7)\). Resposta: D.
-
Se \(I_3\) é a identidade 3×3 e \(B\) é 3×3, então:
- A) \(I_3B=0\)
- B) \(BI_3=B\) e \(I_3B=B\)
- C) \(I_3^T\ne I_3\)
- D) \(\mathrm{tr}(I_3)=1\)
Ver solução
\(I_3\) é elemento neutro: \(BI_3=I_3B=B\); \(\mathrm{tr}(I_3)=3\) e \(I_3^T=I_3\). Resposta: B.
-
Para \(C=\begin{bmatrix}1&2\\3&4\end{bmatrix}\), o traço \(\mathrm{tr}(C)\) é:
- A) 3
- B) 4
- C) 5
- D) 6
Ver solução
\(\mathrm{tr}(C)=1+4=5\). Resposta: C.
-
Se \(D\) é 4×4 e \(d_{ij}=0\) para \(i\ne j\) e \(d_{ii}=7\) para todo \(i\), então \(D\) é:
- A) identidade
- B) nula
- C) diagonal (e escalar)
- D) antissimétrica
Ver solução
Todos os fora da diagonal são 0 e todos os da diagonal são iguais (7). É uma diagonal e também escalar. Resposta: C.
6) Resumo rápido
- Matriz quadrada: ordem \(n\times n\).
- Diagonal principal: \(a_{11},a_{22},\ldots,a_{nn}\); traço é a soma desses termos.
- Diagonal secundária: \(a_{1n},a_{2,n-1},\ldots,a_{n1}\).
- Identidade \(I_n\): 1 na diagonal principal e 0 fora; \(I_nA=AI_n=A\).





















