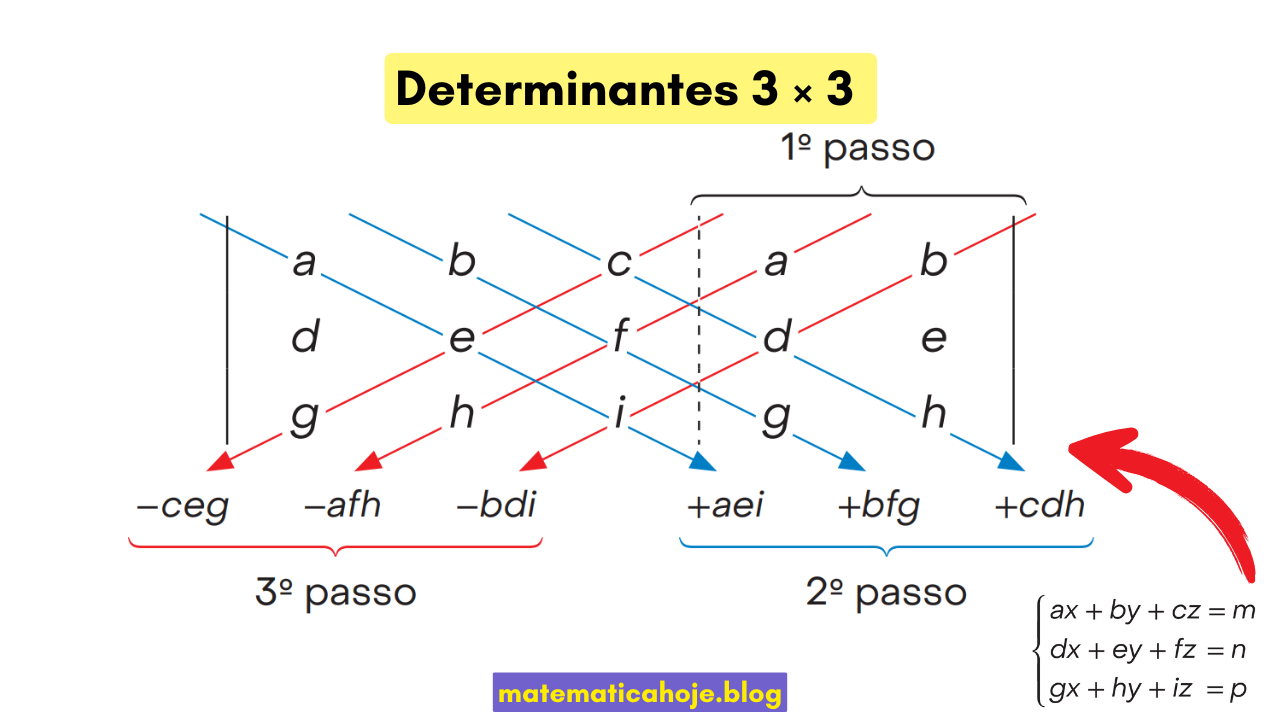
Determinantes 3×3 (Regra de Sarrus)
O determinante de uma matriz \(3\times3\) pode ser calculado pela Regra de Sarrus: some as três diagonais “descendo” e subtraia as três diagonais “subindo”. É essencial para resolver e classificar sistemas \(3\times3\) (Cramer, SPD/SI/SPI). Abaixo, a fórmula, propriedades e um conjunto de exemplos e exercícios com as contas alinhadas um embaixo do outro. Links úteis: determinantes 2×2, A·x=b, sistemas 3×3 e classificação (SPD, SI, SPI).
📘 eBook Fórmulas Matemática — Sarrus, Cramer e Gauss
Resumo visual de \(2\times2\) e \(3\times3\), Regra de Cramer, Rouché–Capelli e eliminação de Gauss/Gauss–Jordan. Ótimo para revisão rápida.
Quero o eBook Praticar no Banco de QuestõesFórmula (Sarrus) para \(3\times3\)
Para \(A=\begin{bmatrix}a&b&c\\ d&e&f\\ g&h&i\end{bmatrix}\):
\(\displaystyle \det(A)=aei+bfg+cdh-\big(ceg+afh+bdi\big)\)
- Repita as duas primeiras colunas à direita.
- Some as diagonais “descendo”: \(aei+bfg+cdh\).
- Subtraia as diagonais “subindo”: \(ceg+afh+bdi\).
Com muitos zeros, a expansão por cofatores também é prática.
Propriedades úteis
- Troca de duas linhas (ou colunas) muda o sinal do determinante.
- Multiplicar uma linha por \(k\) multiplica o determinante por \(k\).
- Se duas linhas forem proporcionais ⇒ \(\det=0\).
- \(\det(A^T)=\det(A)\), \(\det(AB)=\det(A)\det(B)\).
- Triangular \(3\times3\): \(\det=\) produto da diagonal principal.
1) Cálculo direto (Sarrus)
Matriz:
\[ M=\begin{bmatrix} 1 & 2 & 3\\ 0 & -1 & 4\\ 2 & 1 & 5 \end{bmatrix} \]Passo a passo (diagonais ↓ e ↑):
\[ \begin{aligned} S_{+} &= aei + bfg + cdh\\ &= (1)(-1)(5) + (2)(4)(2) + (3)(0)(1)\\ &= -5 + 16 + 0\\[6pt] S_{-} &= ceg + afh + bdi\\ &= (3)(-1)(2) + (1)(4)(1) + (2)(0)(5)\\ &= -6 + 4 + 0\\[6pt] \det(M) &= S_{+} – S_{-}\\ &= 11 – (-2)\\ &= \boxed{13}. \end{aligned} \]Dica: some as três diagonais descendo (S+) e subtraia as três diagonais subindo (S−). Se houver zeros, prefira expansão por cofatores.
2) Quando o determinante zera
\(\begin{bmatrix}1&2&3\\ 2&4&6\\ 0&5&7\end{bmatrix}\)
\[ \begin{aligned} L_2 &= 2L_1 \quad (\text{proporcionalidade})\\ \Rightarrow \det &= 0 \quad (\text{linhas dependentes}). \end{aligned} \]
3) Sistema \(3\times3\) (eliminação rápida)
\(\begin{cases} x+y+z=6\\ 2x-y+z=7\\ -x+2y-z=-1 \end{cases}\)
\[ \begin{aligned} x-2y &= 1 \quad (\text{2ª} – \text{1ª})\\ 3y &= 5 \quad (\text{3ª} + \text{1ª})\\ y &= \tfrac{5}{3}\\ x &= 1 + 2y = 1 + \tfrac{10}{3} = \tfrac{13}{3}\\ z &= 6 – x – y = 6 – \tfrac{13}{3} – \tfrac{5}{3} = 0\\[2pt] \Rightarrow (x,y,z) &= \left(\tfrac{13}{3},\tfrac{5}{3},0\right). \end{aligned} \]
Exercícios (com gabarito — revisado)
1) \(\det\!\begin{bmatrix}2&1&3\\0&-2&5\\4&1&1\end{bmatrix}\)
Gabarito
\[ \begin{aligned} \det &= 2\cdot\det\!\begin{bmatrix}-2&5\\1&1\end{bmatrix} – 1\cdot\det\!\begin{bmatrix}0&5\\4&1\end{bmatrix} + 3\cdot\det\!\begin{bmatrix}0&-2\\4&1\end{bmatrix}\\ &= 2(-7) – 1(-20) + 3(8)\\ &= -14 + 20 + 24\\ &= \boxed{30}. \end{aligned} \]
2) \(\det\!\begin{bmatrix}1&2&3\\2&4&6\\0&5&7\end{bmatrix}\) e interpretação.
Gabarito
\[ \begin{aligned} L_2 &= 2L_1\\ \Rightarrow \det &= 0 \quad (\text{linhas proporcionais ⇒ volume 0}). \end{aligned} \]
3) Resolva \(\{\,x+y+z=6,\ 2x-y+z=7,\ -x+2y-z=-1\,\}\) (Cramer/eliminação).
Gabarito
\[ \begin{aligned} x-2y &= 1\\ 3y &= 5\\ y &= \tfrac{5}{3}\\ x &= \tfrac{13}{3}\\ z &= 0\\[2pt] \Rightarrow (x,y,z) &= \left(\tfrac{13}{3},\tfrac{5}{3},0\right). \end{aligned} \]
4) Para \(A(k)=\begin{bmatrix}1&2&0\\ k&1&3\\ 2&0&1\end{bmatrix}\), calcule \(\det(A(k))\) e diga quando o sistema é SPD.
Gabarito
\[ \begin{aligned} \det(A(k)) &= 1\cdot\det\!\begin{bmatrix}1&3\\0&1\end{bmatrix} – 2\cdot\det\!\begin{bmatrix}k&3\\2&1\end{bmatrix} + 0\cdot(\cdots)\\ &= 1(1) – 2(k-6)\\ &= 1 – 2k + 12\\ &= \boxed{13 – 2k}. \end{aligned} \] \[ \text{SPD}\ \Longleftrightarrow\ \det(A(k))\neq 0\ \Longleftrightarrow\ k\neq \tfrac{13}{2}. \]
5) Use Sarrus para \(\det\!\begin{bmatrix}1&0&2\\3&-1&4\\2&5&1\end{bmatrix}\).
Gabarito
\[ \begin{aligned} \det &= 1\cdot\det\!\begin{bmatrix}-1&4\\5&1\end{bmatrix} – 0\cdot(\cdots) + 2\cdot\det\!\begin{bmatrix}3&-1\\2&5\end{bmatrix}\\ &= 1(-21) + 2(17)\\ &= -21 + 34\\ &= \boxed{13}. \end{aligned} \]
Leia também
Conclusão
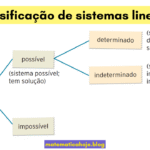
Com a fórmula aei+bfg+cdh − (ceg+afh+bdi) você calcula qualquer determinante \(3\times3\) rapidamente. Se \(\det\neq0\), o sistema associado é SPD (Cramer funciona); se \(\det=0\), aplique Gauss e Rouché–Capelli para decidir entre SI ou SPI.
Precisa de um “resumão”? Baixe o eBook Fórmulas Matemática e pratique no Banco de Questões.