Imagem função exponencial

Imagem (range) da Função Exponencial

Imagem da Função Exponencial

Versão estável e leve (sem bibliotecas externas) — leitura harmônica em qualquer tela.

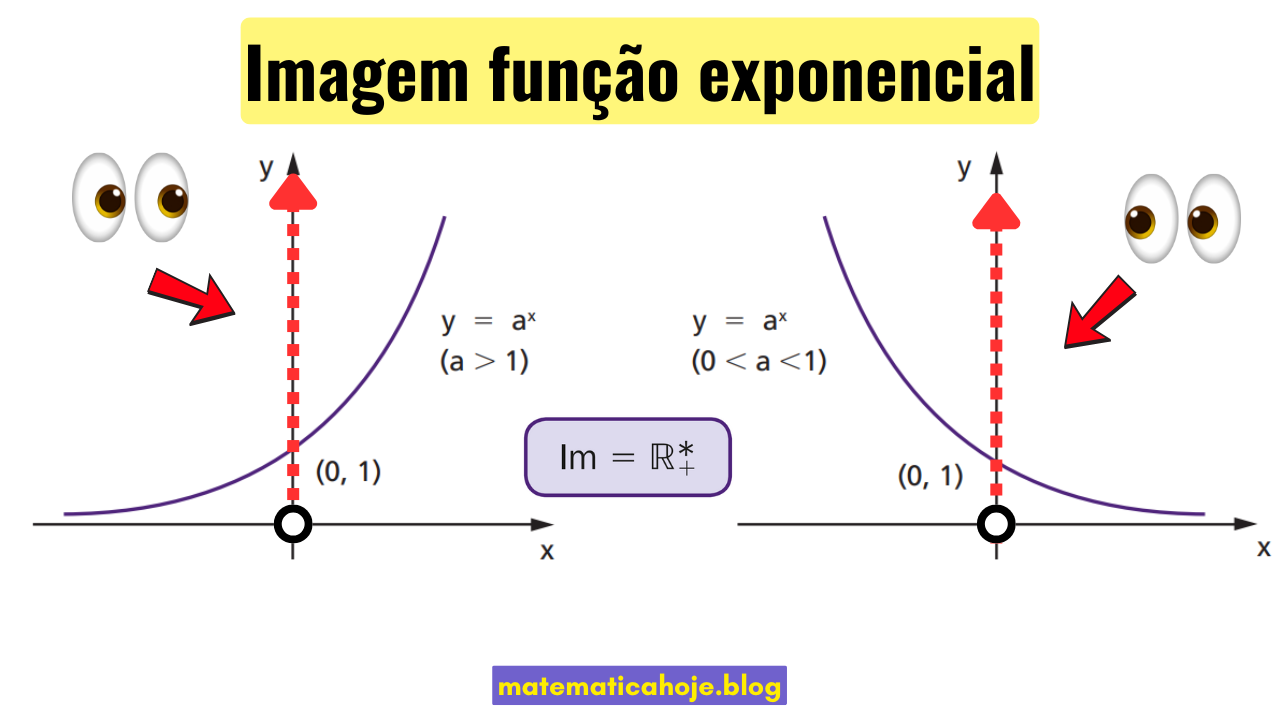
Para a função básica

f(x) = a^x, com a > 0 e a ≠ 1

vale:

Domínio: ℝ (todos os reais).
Imagem: (0, +∞) — sempre positiva.
Assíntota horizontal: y = 0.
Ponto comum do gráfico: (0, 1), pois a⁰ = 1.

Intuição: com base positiva, a potência nunca é zero nem negativa; quando x → −∞, a^x → 0⁺, e quando x → +∞ permanece > 0.

1) Mesma imagem para a > 1 e 0 < a < 1

Seja o gráfico crescente (a > 1) ou decrescente (0 < a < 1), continua valendo:

Im(a^x) = (0, +∞)

O sentido do traço muda; o conjunto de valores possíveis não.

2) Transformações e a imagem

Modelo prático que aparece nos exercícios:

F(x) = A · B^{(x − x₀)} + C (B > 0, B ≠ 1, A ≠ 0)

Assíntota horizontal: y = C.
Imagem:
- Se A > 0: (C, +∞).
- Se A < 0: (−∞, C).

Ex. 1 F(x) = 2 · 3^x − 5 ⇒ A = 2 > 0, C = −5. Assíntota y = −5 e imagem (−5, +∞).

Ex. 2 G(x) = −4 · (1/2)^x + 3 ⇒ A < 0, C = 3. Assíntota y = 3 e imagem (−∞, 3).

📘 Quer um resumo enxuto de funções, gráficos e macetes?
Baixe grátis o eBook Fórmulas Matemática

3) Exercícios de múltipla escolha

(1) A imagem de f(x) = a^x, com a > 0 e a ≠ 1, é:

A) ℝ
B) (−∞, 0)
C) (0, +∞)
D) [0, +∞)

Exponenciais básicas não assumem 0 nem negativos. Resposta: C.

(2) Para F(x) = 3 · 2^x − 7, a imagem é:

A) (−7, +∞)
B) [−7, +∞)
C) (−∞, −7)
D) ℝ

A > 0 e C = −7 ⇒ imagem (C, +∞) = (−7, +∞). Resposta: A.

(3) Para G(x) = −5 · 4^x + 2, a imagem é:

A) (2, +∞)
B) (−∞, 2)
C) [2, +∞)
D) (−∞, +∞)

A < 0 e C = 2 ⇒ imagem (−∞, 2). Resposta: B.

(4) Considere H(x) = (1/2) · 5^x + 4. A imagem é:

A) (4, +∞)
B) [4, +∞)
C) (−∞, 4)
D) (−∞, +∞)

A > 0 e C = 4 ⇒ (4, +∞). Resposta: A.

(5) Para K(x) = −2 · 3^x − 6, assinale a correta:

A) Assíntota y = −6 e imagem (−∞, −6)
B) Assíntota y = −6 e imagem (−6, +∞)
C) Assíntota y = 0 e imagem (−∞, 0)
D) Assíntota y = 0 e imagem (0, +∞)

A < 0 e C = −6 ⇒ assíntota y = −6 e imagem (−∞, −6). Resposta: A.

4) Artigos relacionados

📚 Produtos recomendados

🧠 Mapas Mentais de Matemática 🎯 ENEM Matemática 📚 Coleção 10 eBooks 📝 Banco de Questões 📘 eBook Fórmulas Matemática

Relacionadas

Função Exponencial

Aplicações da Função Exponencial

Crescimento Exponencial

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.