PARALELEPÍPEDO – Geometria Espacial
Volume, Área Total e Diagonal Espacial (com exemplos e exercícios)
O que é um paralelepípedo?
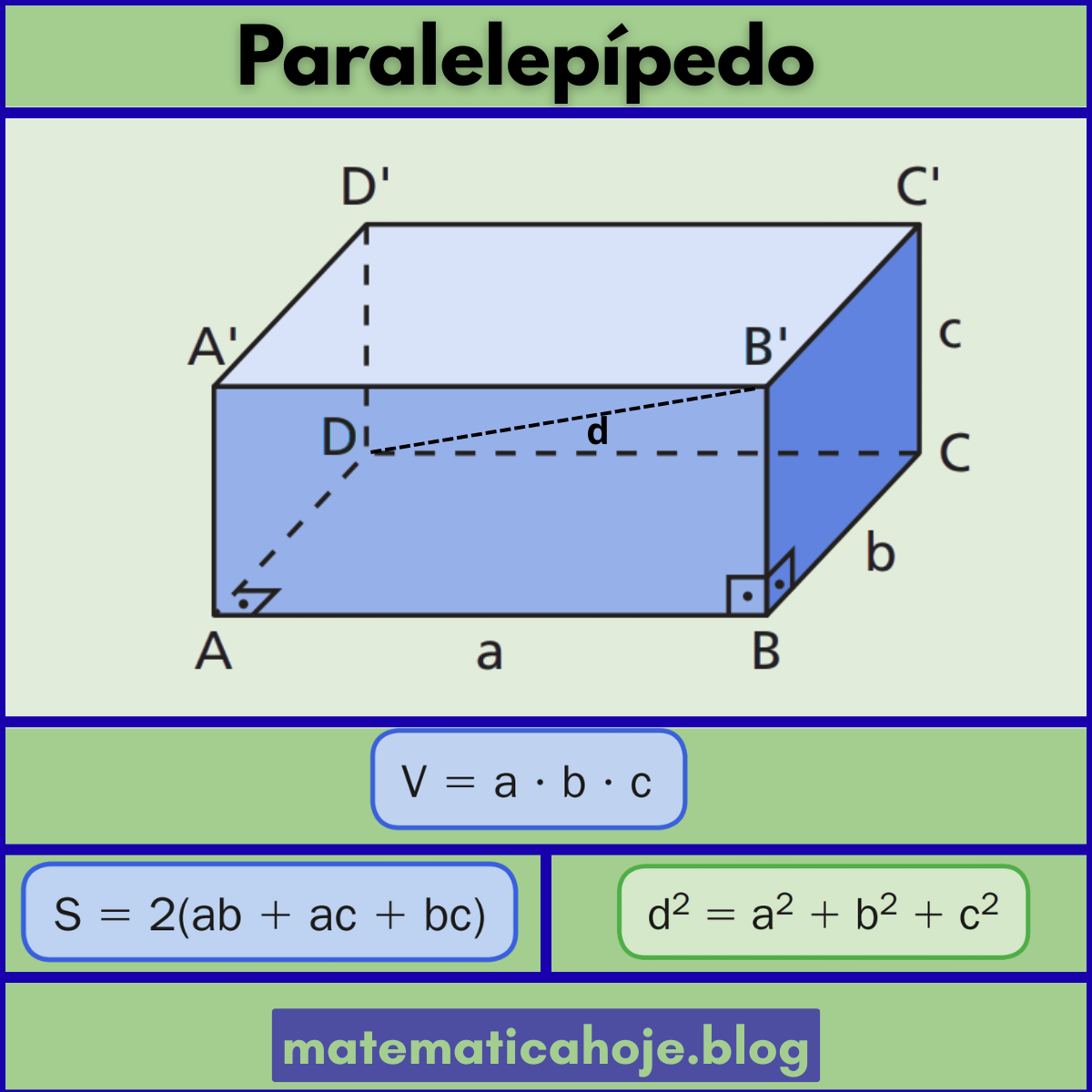
O paralelepípedo retângulo é um prisma cujas faces são retângulos. Possui três dimensões perpendiculares entre si: comprimento \(a\), largura \(b\) e altura \(c\). É uma generalização do cubo (quando \(a=b=c\)).
🧠 Mapas Mentais de Matemática
📘 Banco de Questões
🎯 Guia do ENEM
📚 Coleção completa
📘 Fórmulas do Paralelepípedo
Sejam \(a\), \(b\) e \(c\) as medidas das arestas perpendiculares:
Exemplo 1
Um paralelepípedo retângulo tem dimensões internas \( a=4\,\text{cm}\), \( b=3\,\text{cm}\) e \( c=5\,\text{cm}\). Determine o volume, a área total (todas as 6 faces) e a diagonal espacial.
📗 Baixe o eBook de Fórmulas Matemáticas
Consulte rapidamente todas as fórmulas (Álgebra, Geometria Espacial, Trigonometria e mais) em um único PDF.
📥 Baixar AgoraExemplos Adicionais
Exemplo 2. Uma caixa organizadora (formato de paralelepípedo) tem volume \( V=120\,\text{cm}^3 \) e dimensões da base \( a=5\,\text{cm}\), \( b=4\,\text{cm}\). Calcule a altura \( c \).
Exemplo 3. Um produto precisa caber em uma caixa. Sabe-se que a diagonal interna é \( d=13\,\text{cm} \) e as arestas \( a=3\,\text{cm}\), \( b=4\,\text{cm} \). Determine \( c \).
Exercícios de Múltipla Escolha
1. (Volume) Uma embalagem de medicamento tem o formato de um paralelepípedo retângulo com dimensões internas \( a=2\,\text{cm} \) (comprimento), \( b=3\,\text{cm} \) (largura) e \( c=4\,\text{cm} \) (altura). Desconsidere espessura do material. O volume interno dessa embalagem é:
👀 Ver solução passo a passo
Gabarito: C.
2. (Área total) Uma caixa de presentes será totalmente encapada com papel (todas as 6 faces), sem sobreposição. Suas dimensões internas são \( a=1\,\text{cm}\), \( b=2\,\text{cm}\) e \( c=3\,\text{cm}\). Qual é a área total necessária de papel?
👀 Ver solução passo a passo
Gabarito: B.
3. (Diagonal espacial) Uma barra rígida precisa caber na diagonal interna de uma caixa com medidas \( a=6\,\text{cm}\) (comprimento), \( b=8\,\text{cm}\) (largura) e \( c=3\,\text{cm}\) (altura). O valor da diagonal espacial é:
👀 Ver solução passo a passo
Gabarito: A.
Conclusão
Dominar as fórmulas do paralelepípedo agiliza problemas de volume, área e diagonal em provas de concursos e no ENEM. Para ampliar o estudo, veja também:













