Ângulos em ação: como resolver tudo sem errar no Enem?
Autor: Adriano Rocha • Matemática Hoje
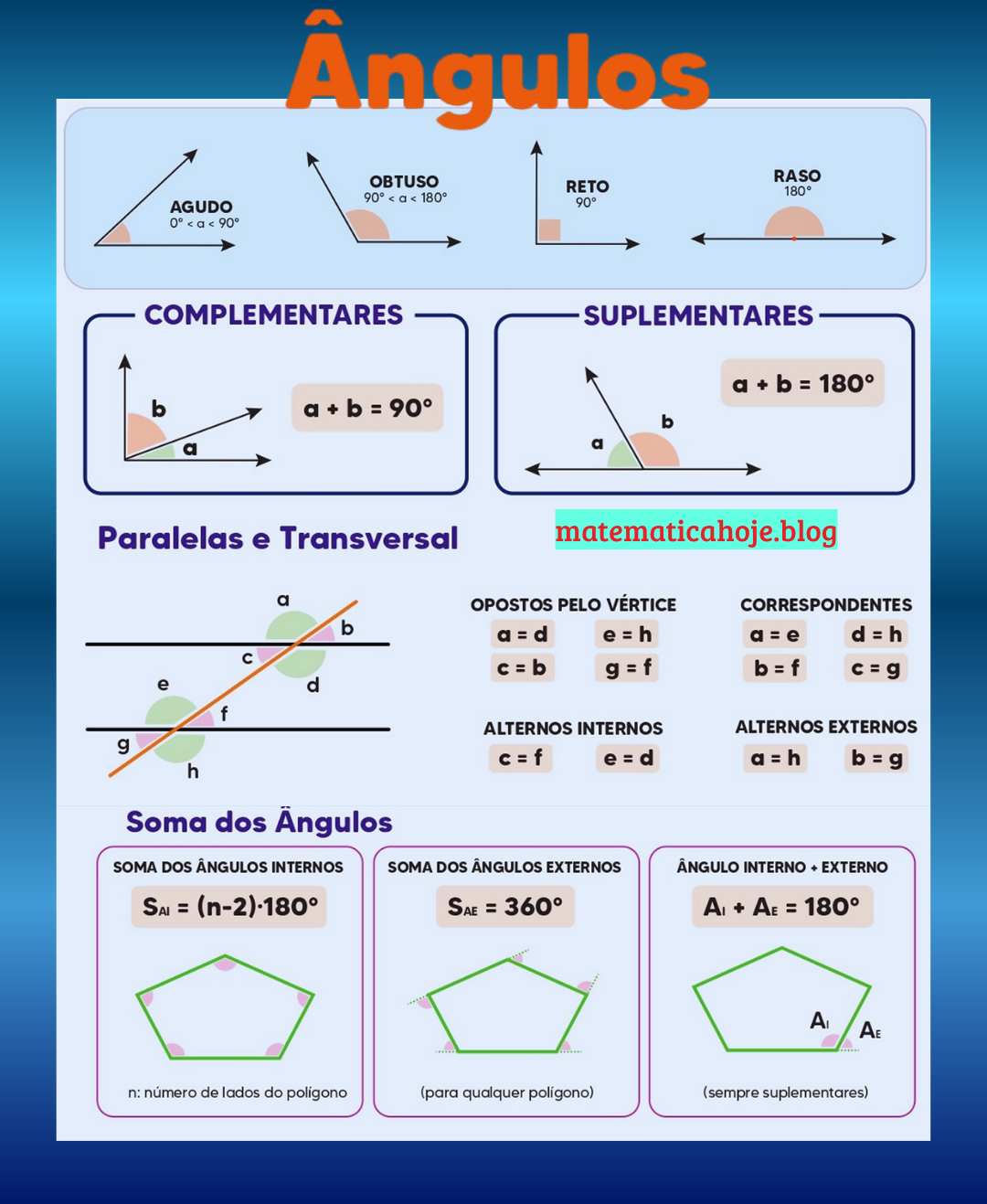
Ângulos aparecem em geometria plana, polígonos, paralelas e transversal e em inúmeros problemas do Enem de Matemática. Neste guia direto ao ponto, você aprende a classificar ângulos (agudo, reto, obtuso e raso), aplicar as relações de complementares e suplementares, usar a transversal em retas paralelas (correspondentes, alternos e opostos pelo vértice) e calcular a soma dos ângulos internos e externos de polígonos. Cada tópico traz exemplos práticos e uma lista de exercícios com solução passo a passo — com a matemática escrita linha por linha após as igualdades para facilitar sua revisão.
Quer todas as fórmulas em um só lugar? Baixe o eBook gratuito e acelere sua revisão.
Baixar eBook de Fórmulas (Grátis)Ângulos: definições, tipos e leitura correta em problemas
| Tipo | Definição | Faixa |
|---|---|---|
| Agudo | abertura pequena | \(0^\circ < \alpha < 90^\circ\) |
| Reto | quarto de volta | \(\alpha=90^\circ\) |
| Obtuso | maior que reto | \(90^\circ < \alpha < 180^\circ\) |
| Raso | meia volta | \(\alpha=180^\circ\) |
Se um ângulo mede \(87^\circ\), ele é agudo. Se mede \(92^\circ\), é obtuso.
Mapas Mentais de Matemática: revisão visual, organizada e pronta para imprimir.
Ver Mapas MentaisComplementares e suplementares: atalho para achar ângulos
Ângulos complementares somam \(90^\circ\): \(a+b=90^\circ\). Ângulos suplementares somam \(180^\circ\): \(a+b=180^\circ\).
O complemento de \(36^\circ\) é \(54^\circ\) e o suplemento de \(136^\circ\) é \(44^\circ\).
Paralelas e transversal: correspondentes, alternos e opostos
Com duas retas paralelas cortadas por uma transversal, valem igualdades como: opostos pelo vértice iguais; correspondentes iguais; alternos internos iguais; alternos externos iguais.
Se um correspondente mede \(68^\circ\), todos os seus iguais (correspondentes/alternos/OPV) também medem \(68^\circ\).
Fortaleça sua base: treine com questões do nosso banco e veja estatísticas de desempenho.
Soma dos ângulos: internos e externos em qualquer polígono
Para um polígono de \(n\) lados: \(S_{\text{internos}}=(n-2)\cdot 180^\circ\) e \(S_{\text{externos}}=360^\circ\). Em cada vértice, interno + externo = \(180^\circ\).
Em um decágono (\(n=10\)): \(S_{\text{internos}}=(10-2)\cdot180^\circ=8\cdot180^\circ=1440^\circ\).
Exemplos resolvidos: do básico ao Enem em minutos
1) Complemento em situação do dia a dia
Enunciado. Aponte o complemento de \(a=27^\circ\).
Ver solução passo a passo
2) Suplementares em placa de trânsito
Enunciado. Se um ângulo é \(132^\circ\), qual o seu suplemento?
Ver solução passo a passo
3) Paralelas e transversal: encontre o x
Enunciado. Em duas paralelas cortadas por transversal, um ângulo correspondente mede \(x+14^\circ\) e o outro mede \(62^\circ\). Ache \(x\).
Ver solução passo a passo
4) Soma dos internos de polígono
Enunciado. Calcule a soma dos ângulos internos de um heptágono.
Ver solução passo a passo
5) Interno + externo em cada vértice
Enunciado. Em um polígono regular, o ângulo externo é \(24^\circ\). Qual é o interno?
Ver solução passo a passo
Lista de exercícios: pratique e confira no abre-fecha
Q1. Determine o complemento de \(41^\circ\).
Mostrar solução
Q2. Ache o suplemento de \(73^\circ\).
Mostrar solução
Q3. Em paralelas, um alterno interno vale \(3x-9^\circ\) e o seu par vale \(2x+6^\circ\). Determine \(x\) e a medida dos ângulos.
Mostrar solução
Q4. Calcule \(S_{\text{internos}}\) de um polígono de 13 lados.
Mostrar solução
Q5. Um triângulo isósceles tem base com ângulo de \(38^\circ\). Encontre os outros dois ângulos.
Mostrar solução
Conclusão: como dominar ângulos para provas e concursos
Você viu como classificar ângulos, aplicar complementares e suplementares, resolver figuras com paralelas e transversal e calcular somas em polígonos. Para fixar, pratique diariamente e use os Mapas Mentais junto ao eBook de Fórmulas. Depois, avance para questões de provas no Banco de Questões e revise nosso guia de Matemática para o Enem.





















