A Função Cosseno
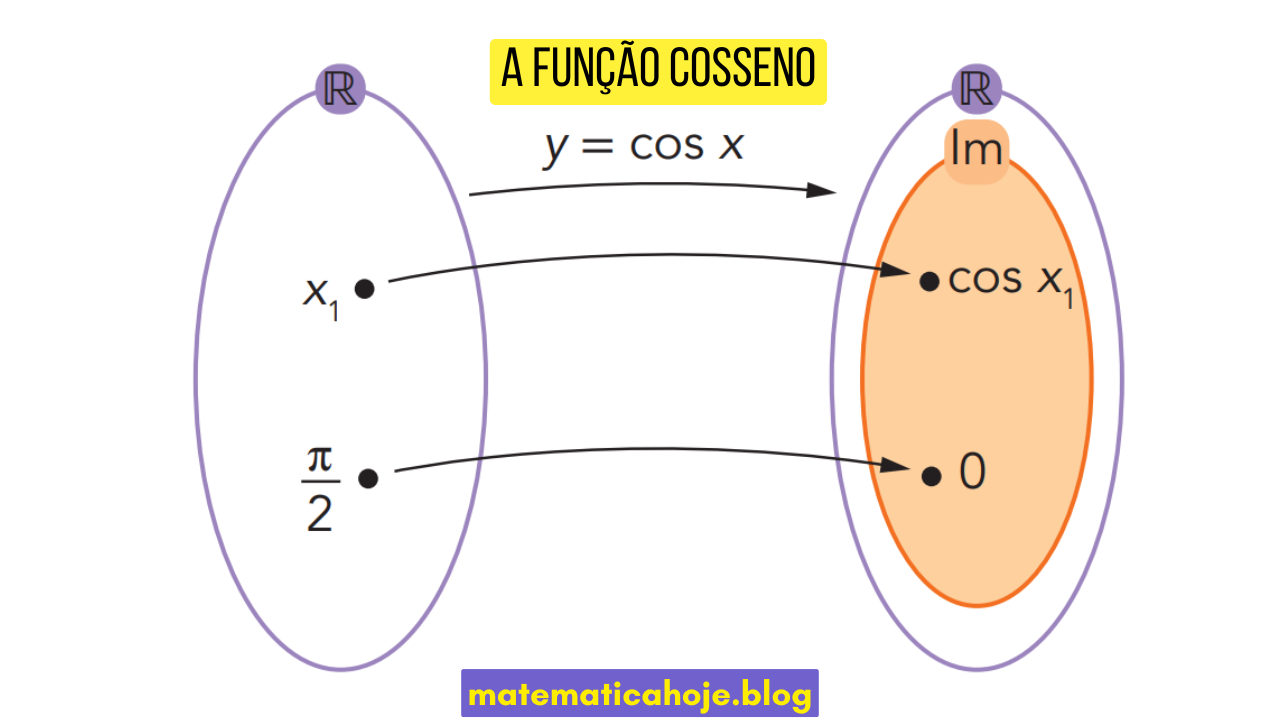
A função cosseno associa cada número real \(x\) ao valor do cosseno desse número. Notação funcional:
\[ f(x)=\cos(x) \]
• Domínio: \(\mathbb{R}\) (todos os reais) • Imagem: \([-1,1]\)
• Período: \(2\pi\) • Paridade: função par \((\cos(-x)=\cos x)\)
Como entender o cosseno
Na circunferência trigonométrica, para cada arco de comprimento \(t\) associamos um ponto \(P(\cos t,\ \sin t)\). A abscissa de \(P\) é o valor de \(\cos t\). Revise a ideia em Seno e cosseno de um número real.
Domínio e Imagem
- Domínio: todos os números reais \((\mathbb{R})\).
- Imagem: \([-1,1]\), pois a projeção horizontal em uma circunferência de raio 1 nunca ultrapassa esse intervalo.
Propriedades Principais
- Período: \(2\pi\) — o gráfico se repete a cada \(2\pi\).
- Função par: \(\cos(-x)=\cos x\) — simétrica em relação ao eixo \(y\).
- Máximos: \(y=1\) em \(x=2k\pi\).
- Mínimos: \(y=-1\) em \(x=\pi+2k\pi\).
- Conexão com ângulos notáveis: veja Ângulos notáveis.
Redução ao 1º quadrante (revisão rápida)
Para facilitar cálculos, reduzimos ângulos dos demais quadrantes a um ângulo agudo do 1º quadrante e aplicamos sinais. Consulte os guias:
Exemplo Resolvido
Calcule \(\cos \dfrac{\pi}{2}\) e \(\cos \pi\).
Passo a passo:
• \(\cos \dfrac{\pi}{2}=0\) (ponto no topo da circunferência — projeção horizontal nula).
• \(\cos \pi=-1\) (ponto à esquerda — projeção horizontal mínima).
Exercícios de Múltipla Escolha
1) O período da função \(y=\cos x\) é:
A) \(\pi\)
B) \(2\pi\)
C) \(\dfrac{\pi}{2}\)
D) \(4\pi\)
Ver solução
O cosseno repete-se a cada \(2\pi\). Resposta: B.
2) Em \(x=0\), temos \(\cos 0=\)
A) 0
B) 1
C) \(-1\)
D) \(\dfrac{\sqrt{2}}{2}\)
Ver solução
No ponto inicial, a abscissa vale 1. Resposta: B.
3) O gráfico de \(y=\cos x\) é simétrico em relação:
A) ao eixo \(x\)
B) à origem
C) ao eixo \(y\)
D) à reta \(y=x\)
Ver solução
Como \(\cos(-x)=\cos x\), é função par — simetria em relação ao eixo \(y\). Resposta: C.






















