A Função Seno
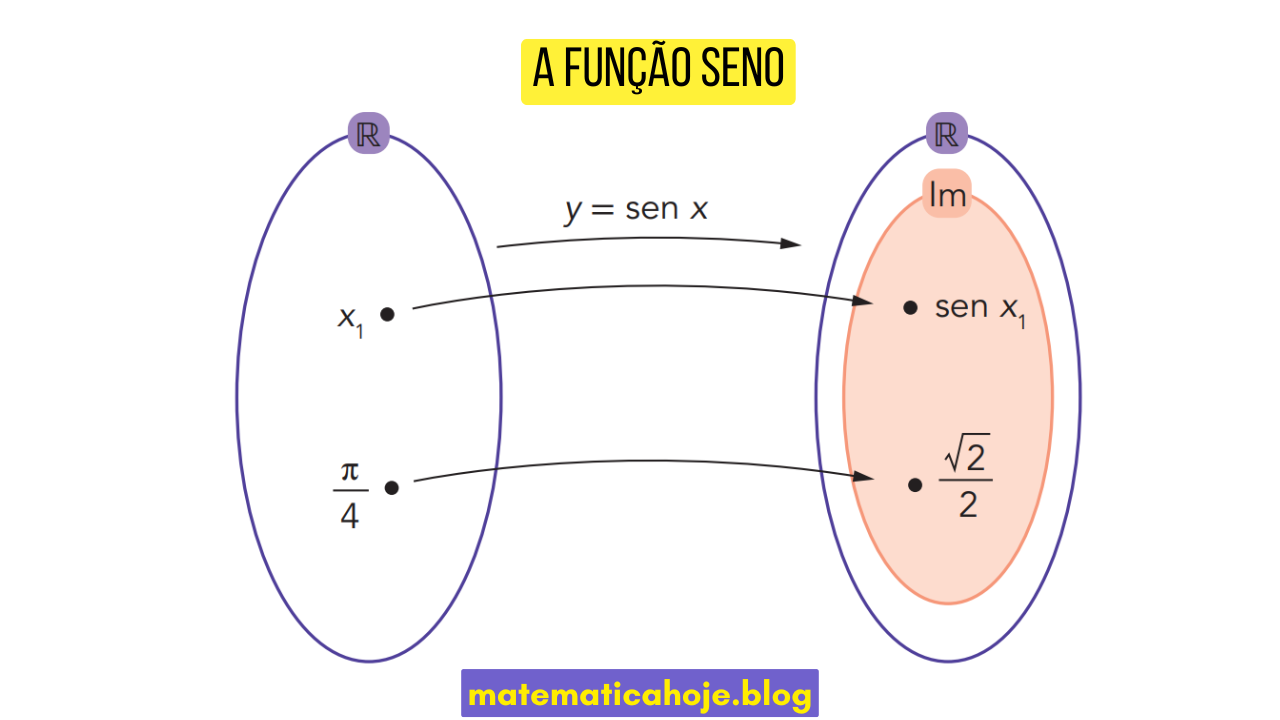
A função seno associa cada número real \(x\) ao valor do seno desse número. Em notação funcional:
\[ f(x) = sen(x) \]Agora que sabemos como obter o valor de seno e de cosseno de números reais, podemos definir as funções trigonométricas, formalizando o que foi estudado até aqui, do ponto de vista de funções.
Assim, dado um número real \(x\), podemos associar a ele o valor do seno de um ângulo com medida de abertura \(x\) radianos (ou de um arco com medida angular \(x\) radianos).
A função trigonométrica seno é a função real com variável real que associa, a cada número real \(x\), o valor real \(sen x\):
\[ f:\ \mathbb{R}\rightarrow \mathbb{R} \] \[ x\ \mapsto\ f(x)=sen x \]
Domínio e Imagem
- Domínio: todos os números reais \(\mathbb{R}\).
- Imagem: intervalo \([-1,\,1]\).
Principais Propriedades
- Período: \(2\pi\) (isto é, \(sen(x+2\pi)=sen(x)\)).
- Função ímpar: \(sen(-x)=-sen(x)\).
- Valores notáveis: \(sen 0 = 0,\ sen\frac{\pi}{2}=1,\ sen\pi=0,\ sen\frac{3\pi}{2}=-1\).
Exemplo Resolvido
Calcule \(sen\!\left(\tfrac{\pi}{4}\right)\).
\[ sen\!\left(\tfrac{\pi}{4}\right)=\tfrac{\sqrt{2}}{2} \]Exercícios de múltipla escolha
1) O valor de \(sen(0)\) é:
A) \(1\)
B) \(0\)
C) \(-1\)
D) \(\tfrac{\sqrt{2}}{2}\)
Ver solução
\(sen(0)=0\). Resposta: B.
2) O valor de \(sen\!\left(\tfrac{\pi}{2}\right)\) é:
A) \(0\)
B) \(-1\)
C) \(1\)
D) \(\tfrac{\sqrt{3}}{2}\)
Ver solução
\(sen\!\left(\tfrac{\pi}{2}\right)=1\). Resposta: C.
3) A imagem da função seno é:
A) \([0,\infty)\)
B) \([-1,1]\)
C) \((-\infty,\infty)\)
D) \([0,1]\)
Ver solução
Os valores de \(sen x\) variam entre \(-1\) e \(1\). Resposta: B.
Continue estudando
Materiais do blog para reforçar trigonometria e revisão:
🧠 Mapas Mentais 📘 ENEM Matemática 📚 10 E-books 🎯 Banco de Questões 👨🏫 Canais Oficiais




















