Aplicações da Função Exponencial

A função exponencial é uma das mais importantes da Matemática, pois descreve fenômenos em que a taxa de variação é proporcional ao próprio valor. Isso significa que a mudança é acelerada, crescendo ou decaindo de forma contínua.

Situações em que a taxa de variação é proporcional ao valor podem ser modeladas por funções exponenciais:

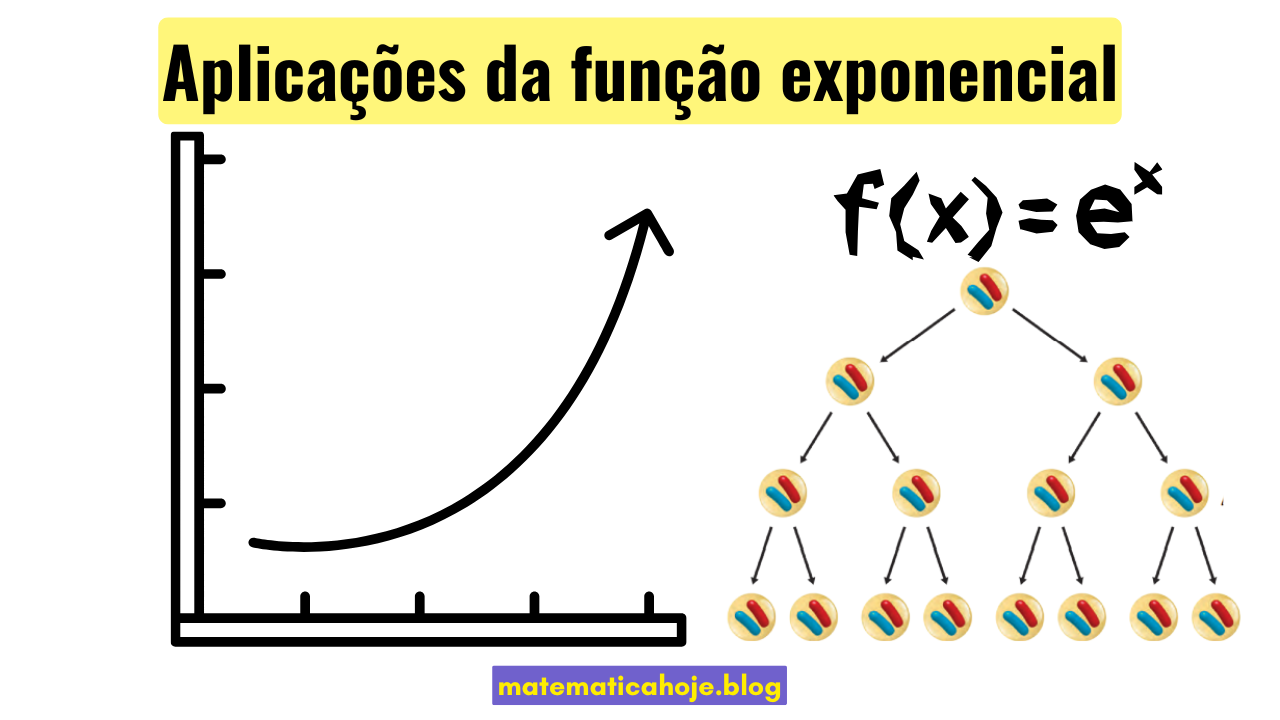
Crescimento: $ Q(t) = Q_0 \cdot a^t, \quad a>1 $
Decaimento: \( Q(t) = Q_0 \cdot b^t, \quad 0

No tempo contínuo: \[ Q(t) = Q_0 \cdot e^{kt}, \quad k>0 \ (\text{crescimento}), \quad k<0 \ (\text{decaimento}) \]

1) Crescimento populacional Biologia

A evolução da população pode ser descrita por: \[ P(t) = P_0 \cdot a^t \] onde $ P_0 $ é a população inicial e $ a $ o fator de crescimento.

Exemplo: População inicial de $20\,000$, com taxa de 3% ao ano: \[ P(5) = 20000 \cdot (1,03)^5 \approx 23186 \]

2) Juros compostos Finanças

O montante em juros compostos é dado por: \[ M = C \cdot (1+i)^t \] onde $ C $ é o capital inicial, $ i $ a taxa de juros e $ t $ o tempo.

Exemplo: Investimento de R\$ 5000 a 8% ao ano durante 4 anos: \[ M = 5000 \cdot (1+0,08)^4 \approx 6802,44 \]

3) Decaimento radioativo Física

A quantidade de material radioativo segue: \[ Q(t) = Q_0 \cdot e^{-\lambda t} \] onde $ \lambda $ é a constante de decaimento.

Exemplo: Uma amostra de 100 g de carbono-14, com meia-vida de 5730 anos. Após esse período: \[ Q(5730) = 100 \cdot \left(\tfrac{1}{2}\right)^1 = 50 \, g \]

4) Resfriamento de corpos Física

De acordo com a lei de resfriamento de Newton: \[ T(t) = T_a + (T_0 – T_a) \cdot e^{-kt} \] onde $ T_a $ é a temperatura ambiente e $ T_0 $ a inicial.

Exemplo: Um café a $90^\circ C$ resfriando em ambiente de $25^\circ C$, após 10 minutos: \[ T(10) = 25 + (90-25) \cdot e^{-0,1 \cdot 10} \approx 49,6^\circ C \]

🔗 Veja também:

Exercícios de Fixação

1. Uma população de 10.000 habitantes cresce a uma taxa de 2% ao ano. Qual será a população em 8 anos?

2. Um capital de R\$ 2000 é aplicado a juros compostos de 5% ao ano. Determine o montante após 6 anos.

3. Um material radioativo reduz sua massa de 80 g para 40 g em 15 dias. Qual a sua meia-vida?

4. Um corpo a $100^\circ C$ é colocado em ambiente de $20^\circ C$. Após 30 minutos sua temperatura é $40^\circ C$. Determine a função exponencial que descreve o resfriamento.

Relacionadas

Crescimento Exponencial

Imagem função exponencial

Propriedades da função exponencial

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.