Arcos e Ângulos em uma Circunferência
O estudo de arcos e ângulos em uma circunferência é fundamental para compreender propriedades geométricas e resolver problemas envolvendo setores circulares, polígonos inscritos e relações trigonométricas.
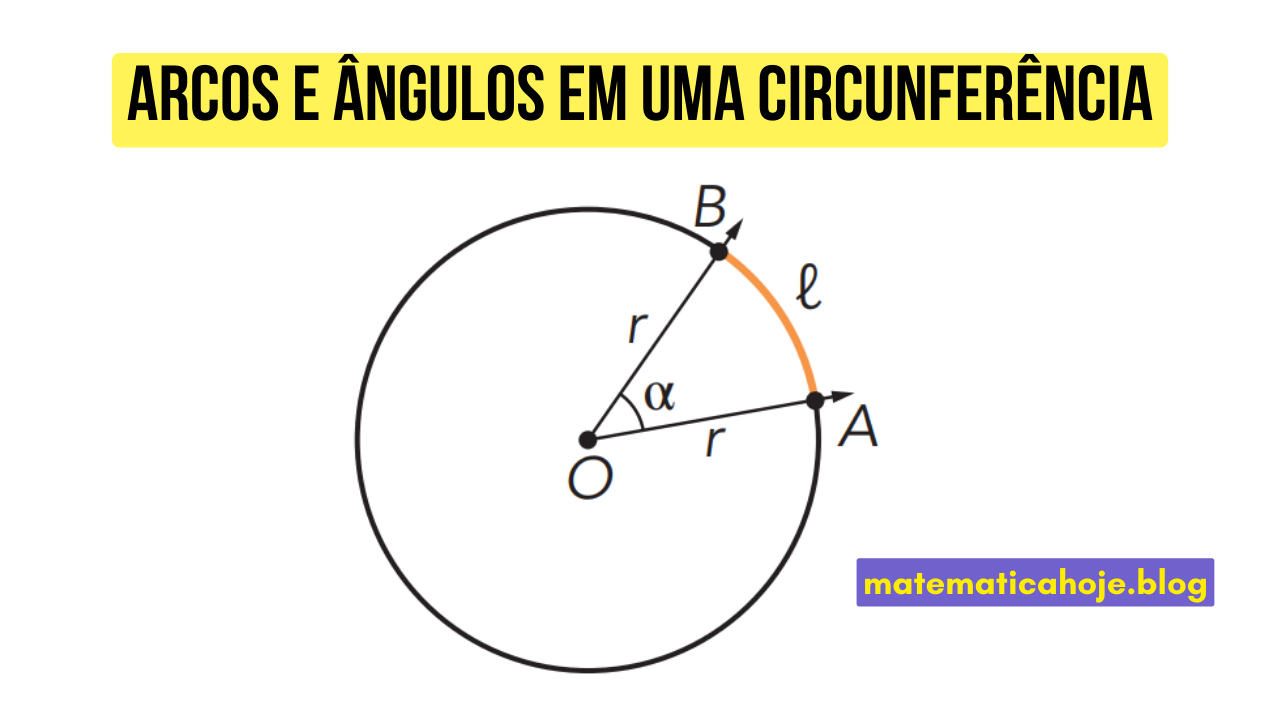
Arco de uma circunferência
O arco é a parte da circunferência compreendida entre dois pontos. Sua medida está diretamente relacionada ao ângulo central correspondente.
Onde:
- \(\ell\) é o comprimento do arco.
- \(r\) é o raio da circunferência.
- \(\alpha\) é o ângulo central em graus.
Ângulos na circunferência
Existem diferentes tipos de ângulos associados à circunferência:
- Ângulo central: tem vértice no centro da circunferência. Sua medida é igual à do arco correspondente.
- Ângulo inscrito: tem vértice sobre a circunferência. Sua medida é metade do arco correspondente.
- Ângulo excêntrico: tem vértice fora da circunferência e relaciona-se com a diferença dos arcos interceptados.
Exemplo resolvido
Exemplo: Uma circunferência tem raio de 5 cm. Calcule o comprimento do arco correspondente a um ângulo central de 72°.
Solução:
Pela fórmula: \(\ell = \frac{\alpha}{360^\circ} \cdot 2\pi r\)
\(\ell = \frac{72}{360} \cdot 2 \pi \cdot 5\)
\(\ell = \frac{1}{5} \cdot 10\pi = 2\pi \approx 6,28\) cm
Exercícios de prática
1) Uma circunferência tem raio de 10 cm. Qual é o comprimento do arco correspondente a um ângulo central de 90°?
- 10π
- 5π
- 15π
- 20π
Ver solução
\(\ell = \frac{90}{360} \cdot 2\pi \cdot 10 = \frac{1}{4} \cdot 20\pi = 5\pi\)
2) O ângulo inscrito que determina um arco de 80° mede:
- 40°
- 80°
- 20°
- 60°
Ver solução
Ângulo inscrito mede a metade do arco correspondente. Portanto, \( \hat{A} = \frac{80}{2} = 40^\circ\).






















