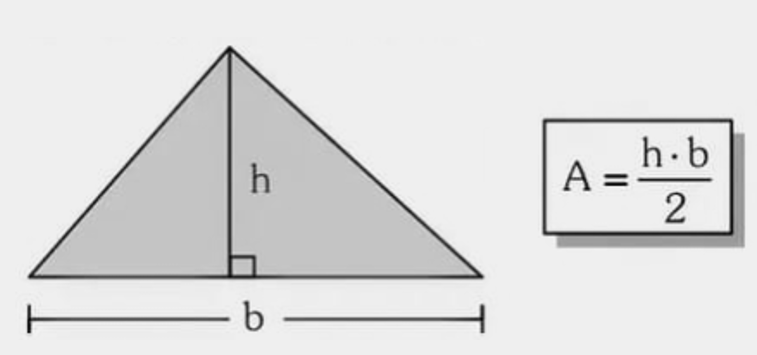
1) Triângulo qualquer (ou obtusângulo)

Fórmula base e altura: \( A=\dfrac{b\cdot h}{2} \). A altura \(h\) é perpendicular à base \(b\); em obtusângulos, ela pode cair fora da figura.

Consulta rápida: area do triangulo, área do triângulo, area triângulo.

Exemplo 1 — Base \(b=10\,\text{cm}\) e altura \(h=6\,\text{cm}\).

Exemplo 2 — \(b=12\,\text{cm}\) e \(h=5{,}2\,\text{cm}\).

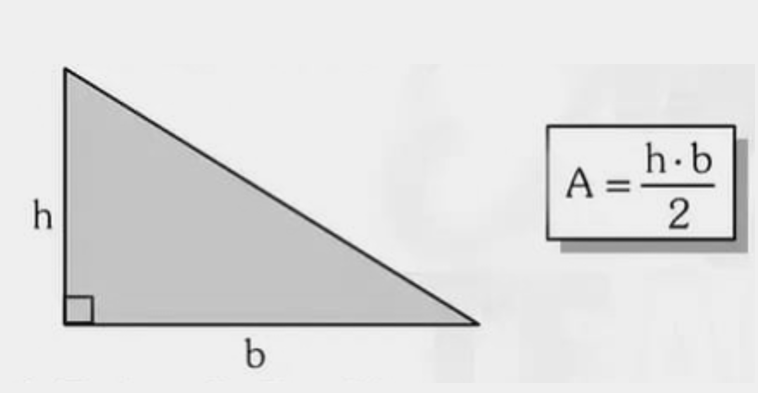
2) Triângulo retângulo (catetos)

Fórmula com catetos: \( A=\dfrac{cat_1\cdot cat_2}{2} \). Relembre o Teorema de Pitágoras.

Exemplo 1 — \(cat_1=9\) e \(cat_2=12\).

Exemplo 2 — \(cat_1=5\) e \(cat_2=7\).

3) Triângulo equilátero

Pelo lado \(L\): \( A=\dfrac{L^{2}\sqrt{3}}{4} \)

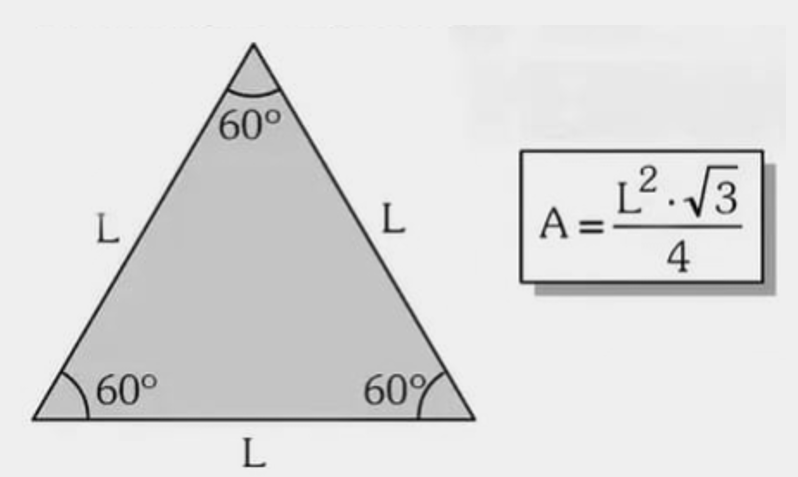
Exemplo 1 — \(L=8\).

Exemplo 2 — \(L=12\).

Pela altura \(h\): \( A=\dfrac{h^{2}\sqrt{3}}{3} \)

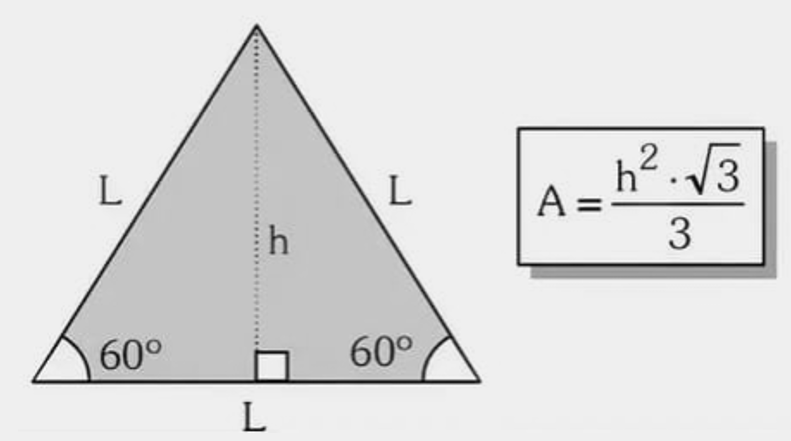
Exemplo 3 — \(h\approx 8{,}66\).

Exemplo 4 — \(h=5{,}5\).

Termos relacionados: área triângulo equilátero, area de um triangulo pela altura.

4) Dois lados e o ângulo compreendido

Regra geral: \( A=\dfrac{ab\sin\theta}{2} \). Veja Lei dos Senos e Lei dos Cossenos.

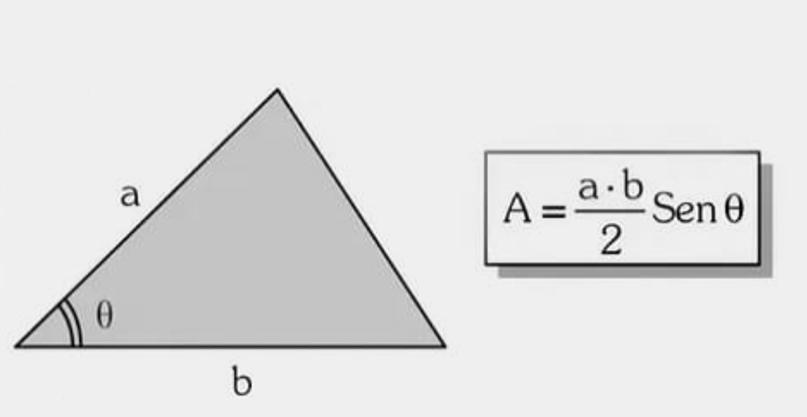
Exemplo 1 — \(a=7\), \(b=10\), \(\theta=30^\circ\).

Exemplo 2 — \(a=12\), \(b=9\), \(\theta=60^\circ\).

5) Três lados conhecidos — Fórmula de Heron

Semiperímetro e área: \( p=\dfrac{a+b+c}{2},\; A=\sqrt{\,p(p-a)(p-b)(p-c)\,} \)

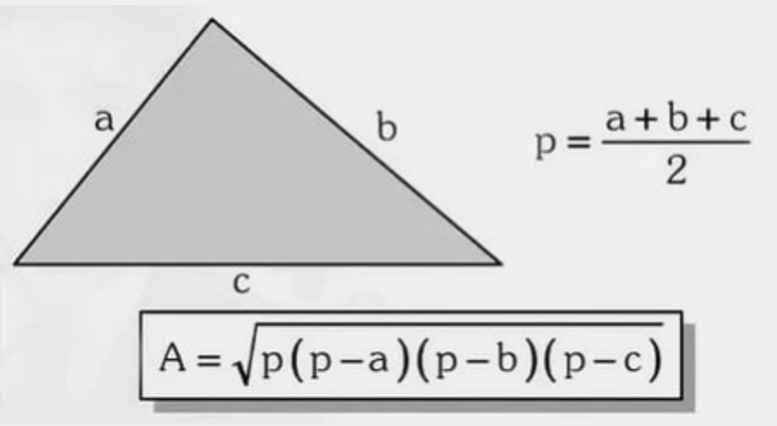
Exemplo 1 — Lados \(7,8,9\).

Exemplo 2 — Lados \(13,14,15\).

6) Triângulo retângulo com altura na hipotenusa

Se a altura à hipotenusa divide-a em segmentos \(m\) e \(n\), então: \( \mathbf{A=m\cdot n} \).

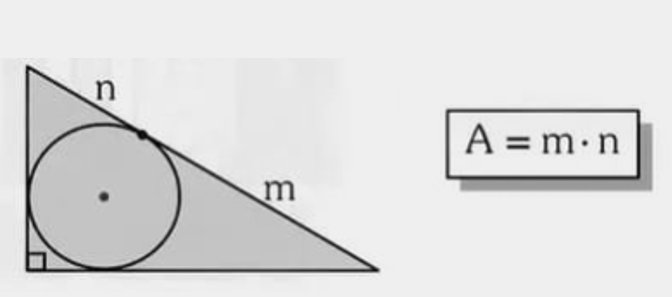
Exemplo 1 — \(m=6\) e \(n=8\).

Exemplo 2 — \(m=3{,}5\) e \(n=7\).

7) Usando o raio da circunferência inscrita (inrádio)

\( A=p\cdot r \), onde \(p\) é o semiperímetro e \(r\) o inrádio. Veja os pontos notáveis.

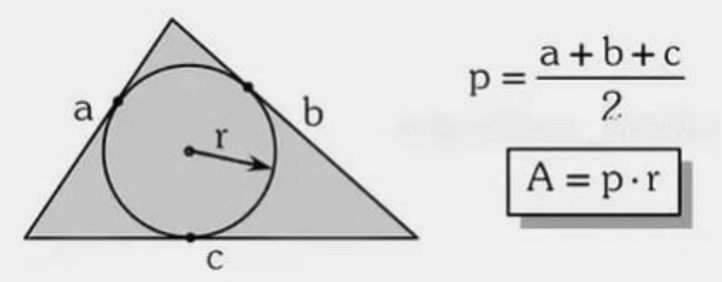
Exemplo 1 — \(p=21\) e \(r=4\).

Exemplo 2 — Triângulo \(6\!-\!8\!-\!10\) com \(p=12\) e \(r=2\).

8) Usando o raio da circunferência circunscrita (circunrádio)

Geral: \( A=\dfrac{abc}{4R} \).

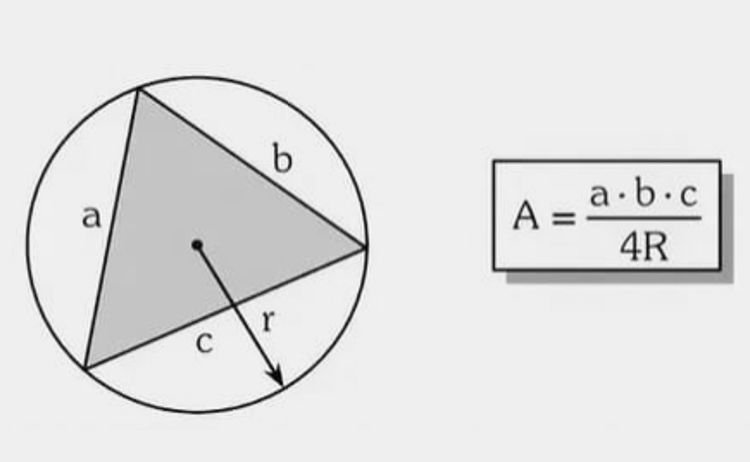
Exemplo 1 — Triângulo \(3\!-\!4\!-\!5\) e \(R=\dfrac{5}{2}\).

Exemplo 2 — Equilátero \(L=10\) e \(R=\dfrac{10}{\sqrt3}\).

Pesquisas relacionadas: area dos triângulos pelo circunrádio \(R\).

Exercícios — Situações-Problema (Múltipla Escolha)

Pratique área do triângulo em contextos reais: base-altura, retângulo, equilátero, dois lados e ângulo, Heron, inrádio, circunrádio, altura na hipotenusa, semelhança e coordenadas. Marque a alternativa correta.

1) Jardim da escola — A equipe de manutenção vai cobrir com manta um canteiro triangular. No croqui, a base vale \(b=12\,\text{cm}\) e a altura vale \(h=7\,\text{cm}\). Qual é a área do canteiro?

1. 36 cm²
2. 40 cm²
3. 42 cm²
4. 44 cm²
5. 48 cm²

2) Placa de advertência — Uma placa triangular retângula possui catetos de 9 m e 14 m. Qual é a área frontal a ser pintada?

1. 54 m²
2. 60 m²
3. 61 m²
4. 63 m²
5. 66 m²

3) Ateliê de mosaico — Azulejos equiláteros de lado L = 10 cm serão encomendados. Qual a área de cada peça?

1. 20√3 cm²
2. 22√3 cm²
3. 24√3 cm²
4. 25√3 cm²
5. 26√3 cm²

4) Agência de design — Um logotipo equilátero deve manter altura h = 6 cm. Qual a área do símbolo?

1. 10√3 cm²
2. 11√3 cm²
3. 12√3 cm²
4. 13√3 cm²
5. 14√3 cm²

5) Lote urbano — Lados medidos a = 8 m, b = 11 m com ângulo de 45°. Qual a área aproximada do lote?

1. 20√2
2. 21√2
3. 22√2
4. 23√2
5. 24√2

6) Vitral histórico — Um vitral triangular tem lados 7 cm, 9 cm e 12 cm. Qual a área para orçamento?

1. 12√5
2. 13√5
3. 14√5
4. 15√5
5. 16√5

7) Ginásio escolar — Será pintado um triângulo com círculo inscrito de raio r = 3 cm. O semiperímetro é p = 18. Qual a área da pintura?

1. 48 cm²
2. 50 cm²
3. 52 cm²
4. 54 cm²
5. 56 cm²

8) Ourivesaria — Um pingente triangular tem lados a = 5 cm, b = 6 cm, c = 7 cm e será montado num aro de raio R = 4 cm. Qual a área do triângulo?

1. 12,500 cm²
2. 12,875 cm²
3. 13,000 cm²
4. 13,125 cm²
5. 13,500 cm²

9) Acessibilidade — Uma rampa forma um triângulo retângulo com o piso. A altura até a hipotenusa divide-a em m = 4 e n = 9. Qual é a área do triângulo da rampa?

1. 30
2. 32
3. 34
4. 35
5. 36

10) Cooperativa agrícola — Um talhão triangular tem base 30 m e altura 22 m. Qual a área plantada?

1. 280 m²
2. 300 m²
3. 330 m²
4. 360 m²
5. 400 m²

11) Planta em escala — Terreno em escala 1:200. No papel, b = 8 cm e h = 5 cm. Qual a área real?

1. 60 m²
2. 70 m²
3. 75 m²
4. 80 m²
5. 90 m²

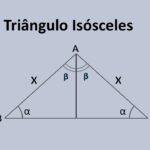
12) Cobertura de beiral — Triângulo isósceles com lados iguais de 10 m e base 12 m. Determine a área do recorte.

1. 44 m²
2. 46 m²
3. 48 m²
4. 50 m²
5. 52 m²

13) Georreferenciamento — Lote com vértices A(0,0), B(6,0), C(2,5). Qual é a área do lote?

1. 12
2. 14
3. 15
4. 16
5. 18

14) Revestimento cerâmico — Triângulo com lados 13, 14 e 15 deve ser coberto por plaquetas de 6 cm² cada. Quantas plaquetas são necessárias (sem perdas)?

1. 12
2. 13
3. 14
4. 15
5. 16

15) Paisagismo — Um canteiro é um triângulo retângulo com catetos 4 m e 6 m. Foi removido um triângulo semelhante de fator 1/2. Qual a área restante?

1. 7 m²
2. 8 m²
3. 9 m²
4. 10 m²
5. 12 m²

Dica: volte ao quadro “Resumo das fórmulas” sempre que precisar relembrar como calcular area do triangulo.

Materiais do Matemática Hoje

• 📘 Mapas Mentais de Matemática
• 🎯 ENEM Matemática Resolvida
• 📚 Coleção 10 eBooks
• 📝 Banco de Questões
• 🔗 Canais Oficiais

Precisa fixar a área do triângulo para provas e concursos? Explore nossos materiais completos.