Os triângulos são uma das figuras geométricas mais fundamentais e têm um papel crucial em várias áreas da matemática e ciências aplicadas. O cálculo da área de um triângulo pode variar dependendo das informações disponíveis e das características do triângulo. Vamos explorar os principais tipos de triângulos e os métodos para calcular sua área.
1. Triângulo Simples
Um triângulo simples é uma figura plana com três lados e três ângulos. A fórmula básica para calcular a área de um triângulo quando se conhece a base e a altura é:
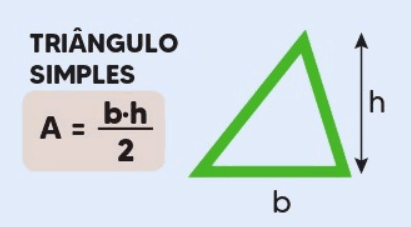
Exemplo:
Se a base de um triângulo é 8 cm e a altura é 5 cm, a área é:
Área = (8 cm×5 cm)/2=20 cm2
2. Triângulo Qualquer
Para triângulos em que não temos a altura diretamente, podemos usar outras fórmulas. Uma delas é a fórmula de Heron, que requer o conhecimento dos três lados do triângulo. Se os lados são a, b e c, primeiro calculamos o semiperímetro p usando:

E então a área A é dada por:

Exemplo:
Para um triângulo com lados 7 cm, 8 cm e 9 cm:
- Calcule o semiperímetro:
p=7+8+92=12
- Use a fórmula de Heron:
A=√12⋅(12−7)⋅(12−8)⋅(12−9)
A=√12⋅5⋅4⋅3
=√720 ≈ 26,83 cm2
3. Triângulo Equilátero
Um triângulo equilátero tem todos os três lados iguais e todos os ângulos de 60 graus. A fórmula da área para um triângulo equilátero com lado a é:

Exemplo:
Para um triângulo equilátero com lado 6 cm:
Área=(62 √3)/4 =(36 √3)/4 = 9√3 ≈ 15,59cm2
4. Ângulo Entre Lados
Se você conhece dois lados de um triângulo e o ângulo entre eles, pode usar a fórmula:
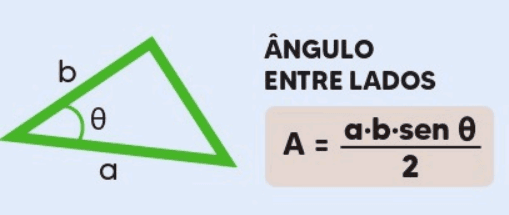
onde a e b são os lados e θ é o ângulo entre eles.
Exemplo:
Para um triângulo com lados 5 cm e 7 cm e o ângulo entre eles de 45 graus:

5. Triângulo Circunscrito
Um triângulo circunscrito é um triângulo em que todos os seus vértices tocam uma circunferência. Para calcular a área, podemos usar a fórmula envolvendo o raio da circunferência circunscrita RRR e os lados a, b e c:

onde a, b e c são os lados do triângulo e R é o raio da circunferência circunscrita.
6. Triângulo Inscrito
Um triângulo inscrito é um triângulo em que sua circunferência está contida dentro de outro triângulo (o triângulo circunscrito). A fórmula para a área de um triângulo inscrito pode ser calculada através da fórmula envolvendo o raio da circunferência inscrita r e o semiperímetro p:


onde r é o raio da circunferência inscrita e p é o semiperímetro.
Exemplo:
Se um triângulo tem semiperímetro de 10 cm e o raio da circunferência inscrita é 4 cm:
Área=4×10=40 cm2
Conclusão
O cálculo da área de um triângulo pode ser feito de várias maneiras, dependendo das informações disponíveis e do tipo de triângulo. Desde o simples triângulo com base e altura conhecidas até triângulos circunscritos e inscritos, cada fórmula fornece uma ferramenta útil para resolver problemas geométricos. Compreender essas fórmulas e quando usá-las é fundamental para resolver problemas de geometria com eficiência.
Leia também
Área de Triângulos: Conceitos e Cálculos
Área de Figuras Planas: Como Calcular, Exercícios Resolvidos
Área de Circunferências: Explorando Formas e Cálculos
Explorando Ângulos: Agudo, Obtuso, Reto e Raso
Retas Paralelas e Transversais
A Soma dos Ângulos em Polígonos: Internos e Externos
Tudo Sobre Triângulos: Classificação e Propriedades
Congruência de Triângulos: Casos e Propriedades
Teorema de Pitágoras: Conceito, Provas e Aplicações
Relações Métricas no Triângulo Retângulo: Conceitos e Fórmulas Essenciais
A Lei dos Senos e a Lei dos Cossenos: Ferramentas Essenciais na Trigonometria
Quadriláteros: Área, Perímetro e Diagonais
Tudo Sobre Circunferência: Conceitos Essenciais e Cálculos
Inscrição e Circunscrição de Triângulos, Quadrados e Hexágonos Regulares
Quadriláteros Circunscritos: Teorema de Pitot
Relação Entre Retas e Circunferências: Corda, Tangente e Encontro de Tangentes
Ângulos na Circunferência: Uma Exploração Completa













