Área do Paralelogramo

Área do Paralelogramo — fórmulas, exemplos e exercícios

Área do Paralelogramo

O paralelogramo é um quadrilátero com dois pares de lados paralelos. Lados opostos são congruentes e ângulos opostos também. A área pode ser obtida por base × altura, por dois lados e o ângulo compreendido ou ainda pela interseção das diagonais.

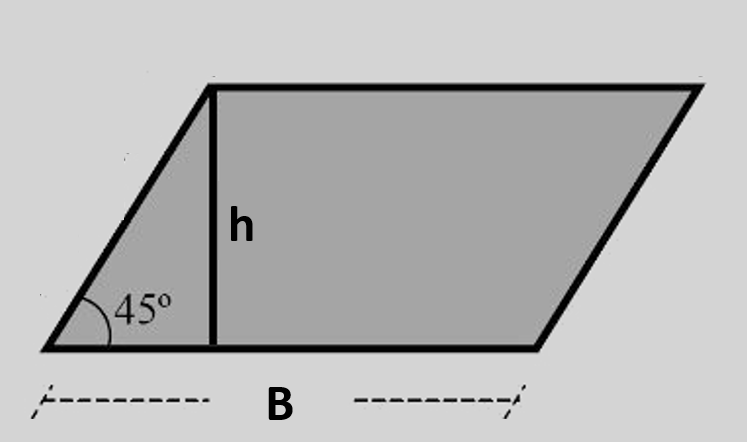
Paralelogramo com base B, altura h e um ângulo de 45°
Área pela altura: \(A=b\cdot h\). A altura é sempre a distância perpendicular entre as bases.
Estude junto: Área do Triângulo (base–altura e \(ab\sin\theta\)), Área do Trapézio, Área do Losango (paralelogramo especial), Lei dos Senos e Lei dos Cossenos.

Fórmulas da área

\[ \textbf{1) Base × altura (paralelogramo):}\quad \boxed{A=b\cdot h} \]
\[ \text{onde }h\text{ é a distância perpendicular entre os lados paralelos} \]
\[ \textbf{2) Dois lados e o ângulo compreendido:}\quad \boxed{A=a\,b\,\sin\theta} \]
\[ \text{(}a\text{ e }b\text{ são lados adjacentes; }\theta\text{ é o ângulo entre eles)} \]
\[ \textbf{3) Pelas diagonais:}\quad \boxed{A=\frac{p\,q}{2}\,\sin\varphi} \]
\[ \text{(}p\text{ e }q\text{ são as diagonais; }\varphi\text{ é o ângulo entre as diagonais)} \]

As três expressões são equivalentes (derivam do produto vetorial e das propriedades das diagonais). Use a que melhor casa com os dados do problema. Para revisar decomposição em triângulos, veja este guia completo de área do triângulo.

Exemplos resolvidos (situação-problema)

1

Área direta por altura

O croqui de um galpão mostra um paralelogramo com base \(b=18\,\text{m}\) e altura \(h=7{,}5\,\text{m}\).

Dados
\(b=18\), \(h=7{,}5\) (m).

Qual é a área do piso?

Ver solução
\[ \begin{aligned} A&=b\cdot h\\ &=18\cdot 7{,}5\\ &=\boxed{135\ \text{m}^2} \end{aligned} \]

Dica: se a altura não vier dada, você pode obtê-la por trigonometria (veja Lei dos Senos e Lei dos Cossenos).

2

Dois lados e ângulo compreendido

Uma placa metálica tem forma de paralelogramo com lados adjacentes \(a=12\,\text{cm}\) e \(b=20\,\text{cm}\). O ângulo entre eles é \(\theta=45^\circ\).

Dados
\(a=12\), \(b=20\) (cm), \(\theta=45^\circ\).

Qual é a área da placa?

Ver solução
\[ \begin{aligned} A&=a\,b\,\sin\theta\\ &=12\cdot 20\cdot \sin 45^\circ\\ &=240\cdot \tfrac{\sqrt{2}}{2}\\ &=\boxed{120\sqrt{2}\ \text{cm}^2}\approx \boxed{169{,}71\ \text{cm}^2} \end{aligned} \]

Compare com o caso do losango (um paralelogramo com lados iguais): área do losango.

3

Pelas diagonais

Um banner publicitário é um paralelogramo cujas diagonais medem \(p=1{,}8\,\text{m}\) e \(q=2{,}6\,\text{m}\). O ângulo entre as diagonais é \(\varphi=60^\circ\).

Dados
\(p=1{,}8\), \(q=2{,}6\) (m), \(\varphi=60^\circ\).

Qual é a área do banner?

Ver solução
\[ \begin{aligned} A&=\frac{p\,q}{2}\,\sin\varphi\\ &=\frac{1{,}8\cdot 2{,}6}{2}\cdot \sin 60^\circ\\ &=\frac{4{,}68}{2}\cdot \tfrac{\sqrt{3}}{2}\\ &=2{,}34\cdot 0{,}866025\ldots\\ &\approx \boxed{2{,}03\ \text{m}^2} \end{aligned} \]

Para revisão de diagonais em quadriláteros especiais, veja losango e trapézio.

4

Altura desconhecida

Em um lote representado como paralelogramo, sabe-se que a área é \(A=216\,\text{m}^2\) e a base é \(b=24\,\text{m}\).

Dados
\(A=216\), \(b=24\) (m).

Qual é a altura \(h\)?

Ver solução
\[ \begin{aligned} A&=b\,h \Rightarrow h=\frac{A}{b}\\ h&=\frac{216}{24}=\boxed{9\ \text{m}} \end{aligned} \]

Problemas de base × altura aparecem também em polígonos regulares (decomposição em triângulos).

Erros comuns (e como evitar)

  • Confundir altura com lado inclinado. Em \(A=b\cdot h\), \(h\) é a distância perpendicular entre as bases; veja a dedução em área do triângulo.
  • Ângulo errado em \(a\,b\,\sin\theta\). \(\theta\) é o ângulo compreendido entre os lados \(a\) e \(b\) (como no triângulo \(A=\tfrac12ab\sin\theta\)).
  • Diagonais. Em \(A=\dfrac{p\,q}{2}\sin\varphi\), \(\varphi\) é o ângulo entre as diagonais, não entre os lados. Compare com o caso do losango.

Exercícios propostos (múltipla escolha)

1

Base e altura

Um piso em forma de paralelogramo tem \(b=14\,\text{m}\) e \(h=6{,}2\,\text{m}\).

A área é:

  • A) \(78{,}4\ \text{m}^2\)
  • B) 86{,}8 \( \text{m}^2\)
  • C) \(92{,}4\ \text{m}^2\)
  • D) \(84{,}0\ \text{m}^2\)
Gabarito
\[ A=b\,h=14\cdot 6{,}2=\boxed{86{,}8\ \text{m}^2}\ (\text{B}) \]
2

Lados e ângulo

Uma chapa tem \(a=9\,\text{cm}\), \(b=17\,\text{cm}\) e \(\theta=30^\circ\) entre eles.

A área é:

  • A) \(68{,}5\ \text{cm}^2\)
  • B) 76{,}5 \( \text{cm}^2\)
  • C) \(153\ \text{cm}^2\)
  • D) \(45\ \text{cm}^2\)
Gabarito
\[ A=a\,b\,\sin 30^\circ=9\cdot 17\cdot \tfrac12=\boxed{76{,}5\ \text{cm}^2}\ (\text{B}) \]
3

Diagonais e ângulo

Num paralelogramo, \(p=10\,\text{cm}\), \(q=13\,\text{cm}\) e \(\varphi=90^\circ\) entre as diagonais.

A área é:

  • A) \(56{,}5\ \text{cm}^2\)
  • B) 65 \( \text{cm}^2\)
  • C) \(130\ \text{cm}^2\)
  • D) \(100\ \text{cm}^2\)
Gabarito
\[ A=\frac{p\,q}{2}\sin\varphi=\frac{10\cdot 13}{2}\cdot 1=\boxed{65\ \text{cm}^2}\ (\text{B}) \]

Mais prática: confira o nosso banco de questões e os mapas mentais de geometria plana.

Materiais do Matemática Hoje

Relacionadas

Área de uma Coroa Circular

Quadrilátero Inscrito na Circunferência

Lei dos Cossenos

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube