Área do Quadrado

Área do Quadrado — fórmulas, exemplos e exercícios

Área do Quadrado

O quadrado é um retângulo com quatro lados iguais e ângulos de 90°. Por isso, suas fórmulas ficam especialmente simples e úteis em problemas de geometria plana.

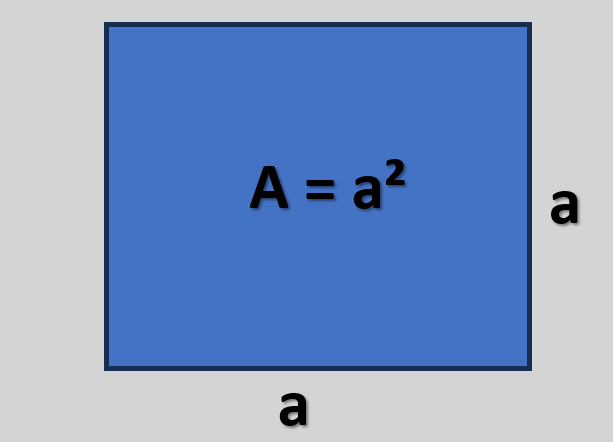
Quadrado com lado a e diagonal d
Quadrado de lado \(a\) e diagonal \(d\). Relação: \(d=a\sqrt{2}\).
Leitura recomendada: Área do Retângulo, Área do Paralelogramo, Área do Losango, Área do Triângulo e Polígonos Regulares.

Fórmulas essenciais (empilhadas)

\[ \textbf{1) Área pelo lado:}\quad \boxed{A=a^2} \]
\[ \textbf{2) Perímetro:}\quad \boxed{P=4a}\qquad \Rightarrow\qquad \boxed{A=\left(\tfrac{P}{4}\right)^2} \]
\[ \textbf{3) Pela diagonal:}\quad d=a\sqrt{2}\ \Rightarrow\ \boxed{A=\frac{d^2}{2}} \]
\[ \textbf{4) Por circunferência inscrita (raio }r\text{):}\quad r=\tfrac{a}{2}\ \Rightarrow\ \boxed{A=(2r)^2=4r^2} \]
\[ \textbf{5) Por circunferência circunscrita (raio }R\text{):}\quad R=\tfrac{a}{\sqrt{2}}\ \Rightarrow\ \boxed{A=(\sqrt{2}R)^2=2R^2} \]

Escolha a expressão que usa diretamente os dados fornecidos no enunciado.

Exemplos resolvidos (situação-problema)

1

Piso quadrado — lado conhecido

Um piso em formato de quadrado tem lado \(a=7\,\text{m}\).

Dados
\(a=7\,\text{m}\).

Qual é a área do piso?

Ver solução
\[ \begin{aligned} A&=a^2\\ &=7^2\\ &=\boxed{49\ \text{m}^2} \end{aligned} \]
2

Lote quadrado — diagonal informada

Um lote quadrado possui diagonal \(d=20\,\text{m}\).

Dados
\(d=20\,\text{m}\).

Qual é a área do lote?

Ver solução
\[ \begin{aligned} A&=\frac{d^2}{2}\\ &=\frac{20^2}{2}\\ &=\frac{400}{2}\\ &=\boxed{200\ \text{m}^2} \end{aligned} \]
3

Quadro — perímetro conhecido

Um quadro quadrado tem perímetro \(P=48\,\text{cm}\).

Dados
\(P=48\,\text{cm}\Rightarrow a=P/4=12\,\text{cm}\).

Qual é a área do quadro?

Ver solução
\[ \begin{aligned} A&=\left(\tfrac{P}{4}\right)^2\\ &=\left(\tfrac{48}{4}\right)^2\\ &=12^2\\ &=\boxed{144\ \text{cm}^2} \end{aligned} \]
4

Tampa com círculo inscrito

Uma tampa quadrada contém uma circunferência inscrita de raio \(r=15\,\text{cm}\).

Dados
\(r=15\,\text{cm}\Rightarrow a=2r=30\,\text{cm}\).

Qual é a área da tampa?

Ver solução
\[ \begin{aligned} A&=(2r)^2\\ &=30^2\\ &=\boxed{900\ \text{cm}^2} \end{aligned} \]

Erros comuns (e como evitar)

  • Confundir diagonal com lado. No quadrado, \(d=a\sqrt{2}\) — use \(A=d^2/2\) se a diagonal for dada.
  • Perímetro ≠ área. Perímetro é \(4a\); área é \(a^2\).
  • Unidades. Converta antes de calcular (ex.: \(1\,\text{m}^2=10\,000\,\text{cm}^2\)).

Para conexões com outras figuras, veja retângulo, paralelogramo e losango.

Exercícios (múltipla escolha)

1

Lado conhecido

Um terreno quadrado tem lado \(a=24\,\text{m}\).

Sua área é:

  • A) \(400\ \text{m}^2\)
  • B) \( \mathbf{576\ \text{m}^2} \)
  • C) \(624\ \text{m}^2\)
  • D) \(720\ \text{m}^2\)
Gabarito
\[ A=a^2=24^2=\boxed{576\ \text{m}^2}\ (\text{B}) \]
2

Diagonal dada

Um mosaico quadrado tem diagonal \(d=28\,\text{cm}\).

A área do mosaico é:

  • A) \(196\ \text{cm}^2\)
  • B) \( \mathbf{392\ \text{cm}^2} \)
  • C) \(448\ \text{cm}^2\)
  • D) \(784\ \text{cm}^2\)
Gabarito
\[ A=\frac{d^2}{2}=\frac{28^2}{2}=\frac{784}{2}=\boxed{392\ \text{cm}^2}\ (\text{B}) \]
3

Perímetro conhecido

A moldura de um quadro quadrado tem perímetro \(P=2{,}4\,\text{m}\).

A área do quadro é:

  • A) \(0{,}20\ \text{m}^2\)
  • B) \(0{,}30\ \text{m}^2\)
  • C) \( \mathbf{0{,}36\ \text{m}^2} \)
  • D) \(0{,}40\ \text{m}^2\)
Gabarito
\[ \begin{aligned} a&=\tfrac{P}{4}=\tfrac{2{,}4}{4}=0{,}6\\ A&=a^2=0{,}6^2=\boxed{0{,}36\ \text{m}^2}\ (\text{C}) \end{aligned} \]
4

Circunferência inscrita

Um selo quadrado contém uma circunferência inscrita de raio \(r=2{,}5\,\text{cm}\).

A área do selo é:

  • A) \(16\ \text{cm}^2\)
  • B) \(20\ \text{cm}^2\)
  • C) \( \mathbf{25\ \text{cm}^2} \)
  • D) \(36\ \text{cm}^2\)
Gabarito
\[ A=(2r)^2=(2\cdot 2{,}5)^2=5^2=\boxed{25\ \text{cm}^2}\ (\text{C}) \]

Mais prática: veja o nosso banco de questões e os mapas mentais de geometria.

Materiais do Matemática Hoje

Relacionadas

Teorema das Projeções

Relação Fundamental do Triângulo Retângulo

Igualdade entre pares de ângulos opostos no Triângulo

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube