Área do Setor Circular e Comprimento do Arco
Fórmulas com graus e radianos, conversões, exemplos resolvidos e exercícios de múltipla escolha com gabarito.
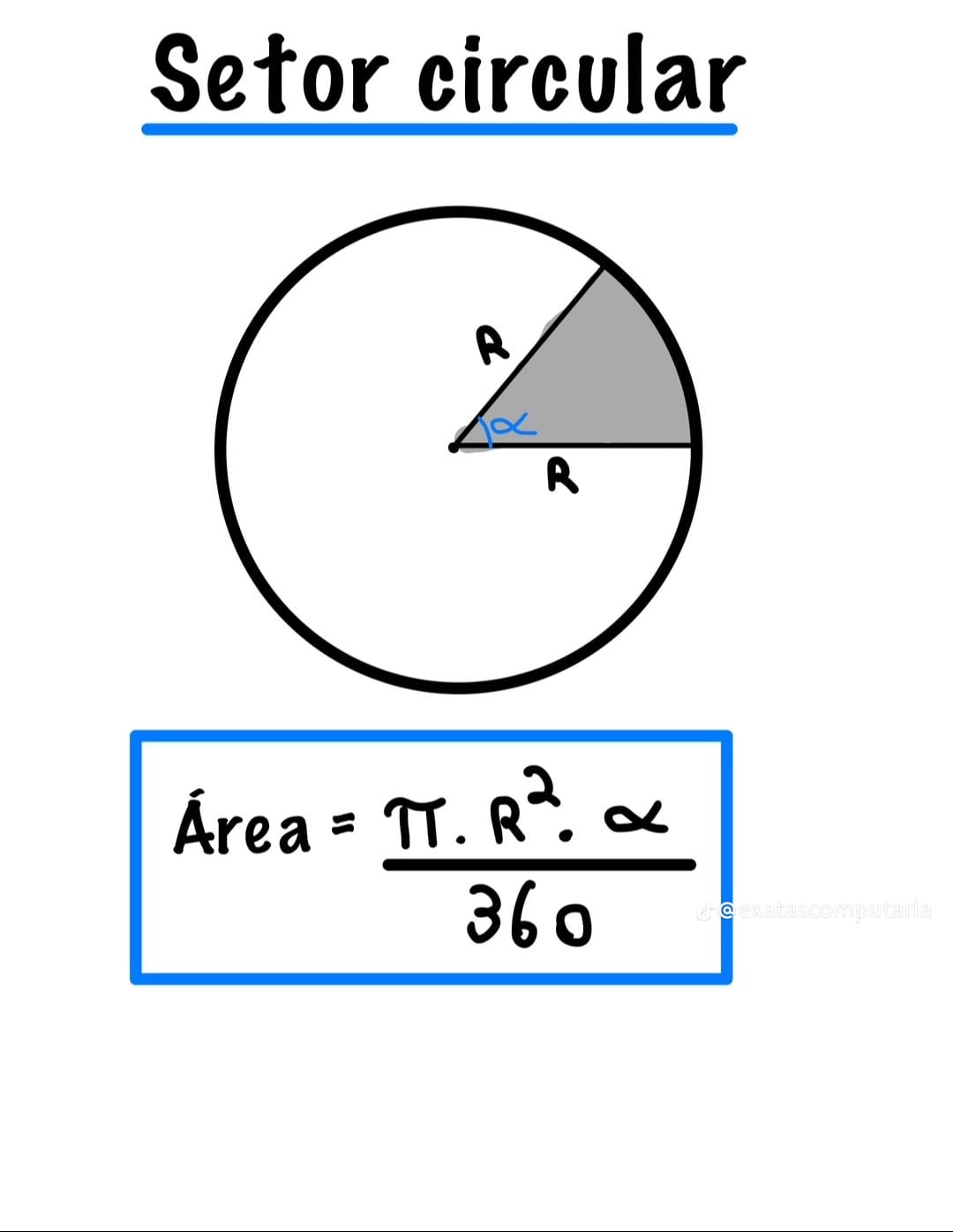
Fórmulas essenciais
Área do setor (graus)
\[ A=\frac{\theta}{360^\circ}\,\pi R^2 \]
Use quando \(\theta\) estiver em graus.
Área do setor (radianos)
\[ A=\frac{\theta_{\text{rad}}}{2}\,R^2 \]
Use quando \(\theta\) estiver em radianos.
Comprimento do arco
\[ L=\frac{\theta}{360^\circ}\,2\pi R \quad\text{ou}\quad L=\theta_{\text{rad}}\,R \]
Conversão de ângulo
\[ \theta_{\text{rad}}=\theta_{\text{graus}}\cdot\frac{\pi}{180^\circ} \qquad \theta_{\text{graus}}=\theta_{\text{rad}}\cdot\frac{180^\circ}{\pi} \]
Reforce o conteúdo com: ENEM Matemática • Mapas Mentais • Banco de Questões
📘 Fórmulas sempre à mão
Baixe o eBook Fórmulas Matemática e tenha um resumo rápido de áreas, perímetros e relações trigonométricas.
Exemplos resolvidos
Exemplo 1 graus
Num círculo de raio \(R=6\,\text{cm}\), o ângulo central é \(\theta=60^\circ\). Calcule a área do setor e o comprimento do arco (use \(\pi\approx3{,}14\)).
Ver solução
\(=\dfrac{60^\circ}{360^\circ}\cdot 3{,}14\cdot 6^2\)
\(=\dfrac{1}{6}\cdot 3{,}14\cdot 36\)
\(=18{,}84\,\text{cm}^2\).
Arco: \(L=\dfrac{\theta}{360^\circ}\,2\pi R\)
\(=\dfrac{60^\circ}{360^\circ}\cdot 2\cdot 3{,}14\cdot 6\)
\(=\dfrac{1}{6}\cdot 37{,}68\)
\(=6{,}28\,\text{cm}\).
Exemplo 2 radianos
Para \(R=10\,\text{m}\) e \(\theta=2\,\text{rad}\), determine a área do setor.
Ver solução
\(=\dfrac{2}{2}\cdot 10^2\)
\(=1\cdot 100\)
\(=100\,\text{m}^2\).
Exemplo 3 ângulo a partir da área
Um setor de raio \(R=12\,\text{cm}\) tem área \(A=60\pi\,\text{cm}^2\). Encontre o ângulo central em graus.
Ver solução
\(\theta=\dfrac{360^\circ\cdot 60\pi}{\pi\cdot 12^2}\)
\(\theta=\dfrac{21600^\circ}{144}\)
\(\theta=150^\circ\).
Exercícios de múltipla escolha (com gabarito)
Enunciados claros e soluções com os passos um abaixo do outro após cada “=”. Considere \(\pi\approx 3{,}14\) quando indicado.
1) Um círculo tem \(R=7\,\text{cm}\) e \(\theta=90^\circ\). A área do setor é, aproximadamente:
Gabarito e solução
\(=\dfrac{1}{4}\cdot \pi\cdot 49\)
\(=12{,}25\pi\)
\(\approx 38{,}5\,\text{cm}^2\Rightarrow\) Letra C.
2) Para \(R=5\,\text{cm}\) e \(\theta=72^\circ\), o comprimento do arco é:
Gabarito e solução
\(=\dfrac{1}{5}\cdot 10\pi\)
\(=2\pi\)
\(\approx 6{,}28\,\text{cm}\Rightarrow\) Letra B.
3) Um setor de raio \(12\,\text{cm}\) tem área \(60\pi\,\text{cm}^2\). O ângulo central \(\theta\) (em graus) vale:
Gabarito e solução
\(=\dfrac{360^\circ\cdot 60\pi}{\pi\cdot 144}\)
\(=\dfrac{21600^\circ}{144}\)
\(=150^\circ\Rightarrow\) Letra C.
4) Com \(R=9\,\text{m}\) e \(\theta=1{,}2\,\text{rad}\), o arco mede:
Gabarito e solução
\(=1{,}2\cdot 9\)
\(=10{,}8\,\text{m}\Rightarrow\) Letra B.
5) Dado um arco de comprimento \(L=8\pi\,\text{cm}\) em um círculo de raio \(R=4\,\text{cm}\), a área do setor é:
Gabarito e solução
\(=2\pi\) (círculo completo).
\(A=\dfrac{\theta_{\text{rad}}}{2}R^2\)
\(=\dfrac{2\pi}{2}\cdot 4^2\)
\(=\pi\cdot 16\)
\(=16\pi\,\text{cm}^2\Rightarrow\) Letra C.
6) A área de um setor é \(25\pi\,\text{cm}^2\) quando \(\theta=90^\circ\). O raio vale:
Gabarito e solução
\(25\pi=\dfrac{1}{4}\pi R^2\)
\(R^2=100\)
\(R=10\,\text{cm}\Rightarrow\) Letra C.
7) Uma pizza de raio \(14\,\text{cm}\) é cortada em um setor de \(\theta=30^\circ\). A área desse pedaço é aprox.:
Gabarito e solução
\(=\dfrac{1}{12}\cdot \pi\cdot 196\)
\(=\dfrac{196}{12}\pi=\dfrac{49}{3}\pi\)
\(\approx 51{,}3\,\text{cm}^2\Rightarrow\) Letra C.
8) Em um círculo de raio \(10\,\text{m}\), o arco mede \(5\pi\,\text{m}\). O ângulo central vale:
Gabarito e solução
\(=\dfrac{\pi}{2}\,\text{rad}\)
\(\theta_{\text{graus}}=\dfrac{\pi}{2}\cdot\dfrac{180^\circ}{\pi}\)
\(=90^\circ\Rightarrow\) Letra C.
Dicas finais
- Decida primeiro a unidade do ângulo: graus ou radianos (isso muda a fórmula).
- Arco e setor são proporcionais ao ângulo: dobrando \(\theta\), dobra \(L\) e \(A\).
- Para questões mistas, converta para radianos: \(L=\theta R\) costuma ser mais rápido.













