O Arranjo Simples é um dos temas centrais da Análise Combinatória. Ele aparece quando escolhemos p elementos dentre n disponíveis e, principalmente, quando a ordem importa (muda o resultado).
Arranjo é o “meio do caminho” entre contar possibilidades etapa a etapa (PFC) e aplicar fórmulas clássicas como permutações e combinações.
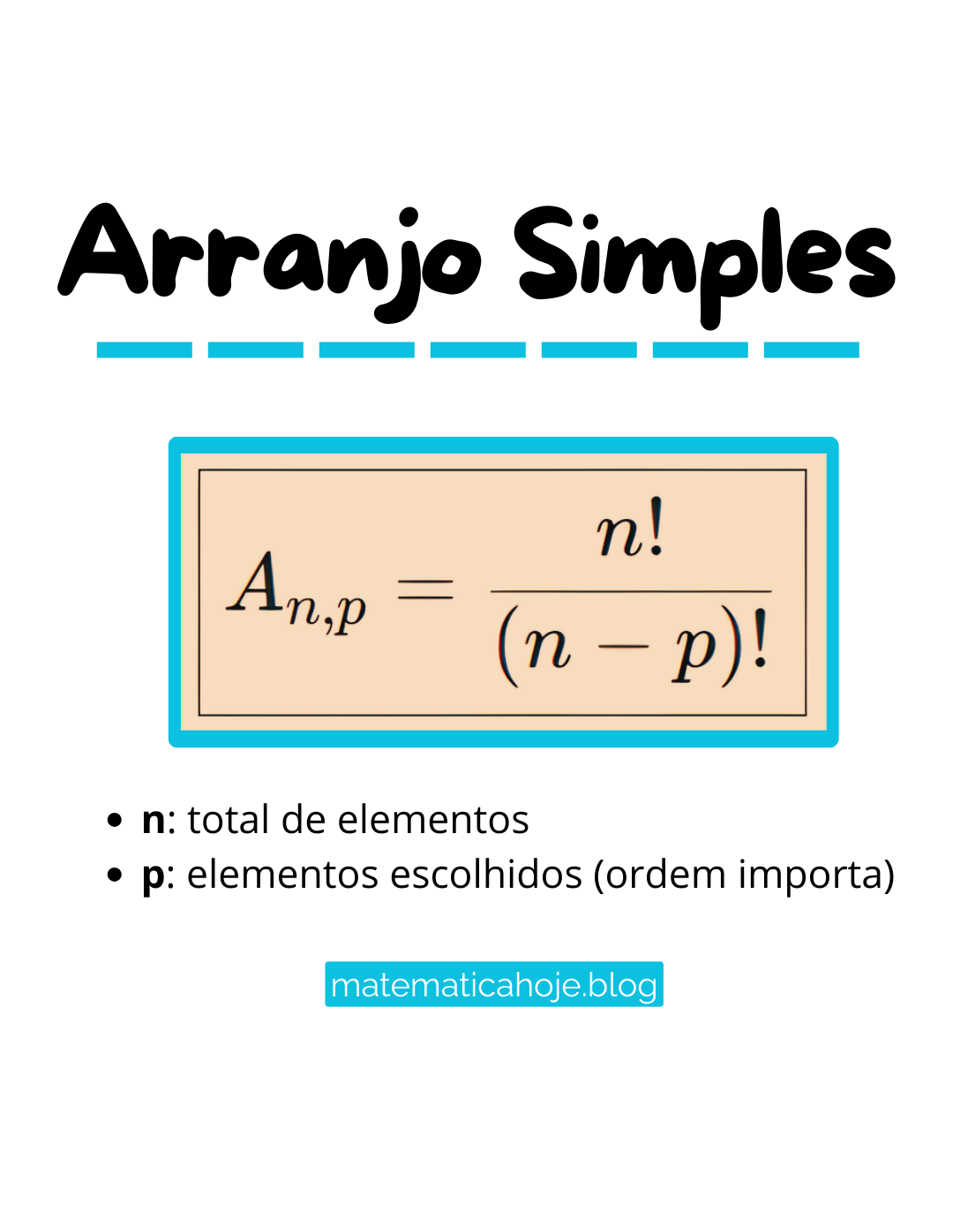
O que é Arranjo Simples?
Em um arranjo simples, nós:
- temos n elementos disponíveis (total);
- escolhemos p elementos (selecionados);
- a ordem importa (por isso é arranjo, e não combinação).
Ele pode ser entendido diretamente pelo Princípio Fundamental da Contagem : na 1ª escolha temos n opções, na 2ª temos n-1, e assim por diante, até completar p escolhas.
Usando fatorial, chegamos à forma mais usada:
Quando usar Arranjo Simples?
Use arranjo quando:
- você escolhe parte dos elementos (\(p<n\));
- não há repetição (cada elemento escolhido sai do “conjunto”);
- a ordem muda o resultado (ex.: ranking, senha, pódio, cargos).
Se você escolhe todos os elementos (\(p=n\)), vira permutação simples. Se a ordem não importa, geralmente é combinação simples. E se houver repetição controlada, pode entrar em permutação com repetição.
Exemplos resolvidos
Exemplo 1: De quantas formas podemos formar um código com 2 letras distintas escolhidas entre 5 letras?
Ver solução
Temos \(n=5\) e \(p=2\). Como a ordem importa (AB ≠ BA), é arranjo:
\[ A_{5,2}=\frac{5!}{(5-2)!}=\frac{5!}{3!}=\frac{5\cdot 4\cdot 3!}{3!}=20 \]Resposta: \(\boxed{20}\).
Exemplo 2: Um pódio (1º, 2º e 3º) será formado com 8 atletas. Quantas possibilidades?
Ver solução
Aqui \(n=8\) e \(p=3\). A ordem importa (1º, 2º, 3º), então:
\[ A_{8,3}=\frac{8!}{(8-3)!}=\frac{8!}{5!}=\frac{8\cdot 7\cdot 6\cdot 5!}{5!}=336 \]Resposta: \(\boxed{336}\).
Exercícios resolvidos
Exercício 1
De quantas formas podemos escolher e ordenar 4 pessoas para ocupar 2 cargos diferentes (Presidente e Vice)?
Ver solução
Como os cargos são diferentes, a ordem importa. Logo, é arranjo:
\[ A_{4,2}=\frac{4!}{(4-2)!}=\frac{4!}{2!}=\frac{4\cdot 3\cdot 2!}{2!}=12 \]Resposta: \(\boxed{12}\).
Exercício 2
Quantas senhas de 3 algarismos distintos podem ser formadas com os dígitos 0 a 9, sem repetir dígitos?
Ver solução
Escolhemos 3 elementos dentre 10, com ordem importando:
\[ A_{10,3}=\frac{10!}{7!}=10\cdot 9\cdot 8=720 \]Resposta: \(\boxed{720}\).
Exercício 3
De quantas formas podemos formar um “top 5” com 12 candidatos?
Ver solução
Top 5 é ranking, então a ordem importa:
\[ A_{12,5}=\frac{12!}{7!}=12\cdot 11\cdot 10\cdot 9\cdot 8=95040 \]Resposta: \(\boxed{95040}\).
Conexões importantes (para avançar)
O arranjo simples conversa diretamente com o coeficiente binomial (quando a ordem deixa de importar), com o número binomial e com o Triângulo de Pascal, que organizam combinações de forma estruturada.
Para consolidar o tema dentro do seu estudo, a sequência mais eficiente costuma ser: PFC → Fatorial → Arranjo → Permutação → Combinação.
Arranjo Simples no ENEM e concursos
Em provas, o arranjo simples aparece em situações como pódios, senhas, códigos, ordens de chamada, posições em fila e escolhas com cargos diferentes. Se quiser um guia completo, acesse: Análise Combinatória — Guia Completo .
Continue seus estudos com o Matemática Hoje:
Mapas Mentais eBook de Fórmulas (Grátis) Banco de Questões Coleção 10 eBooks
























