Classificação de Triângulos quanto aos Ângulos

Classificação angular: ΔDEF acutângulo, ΔABC retângulo e ΔRST obtusângulo.

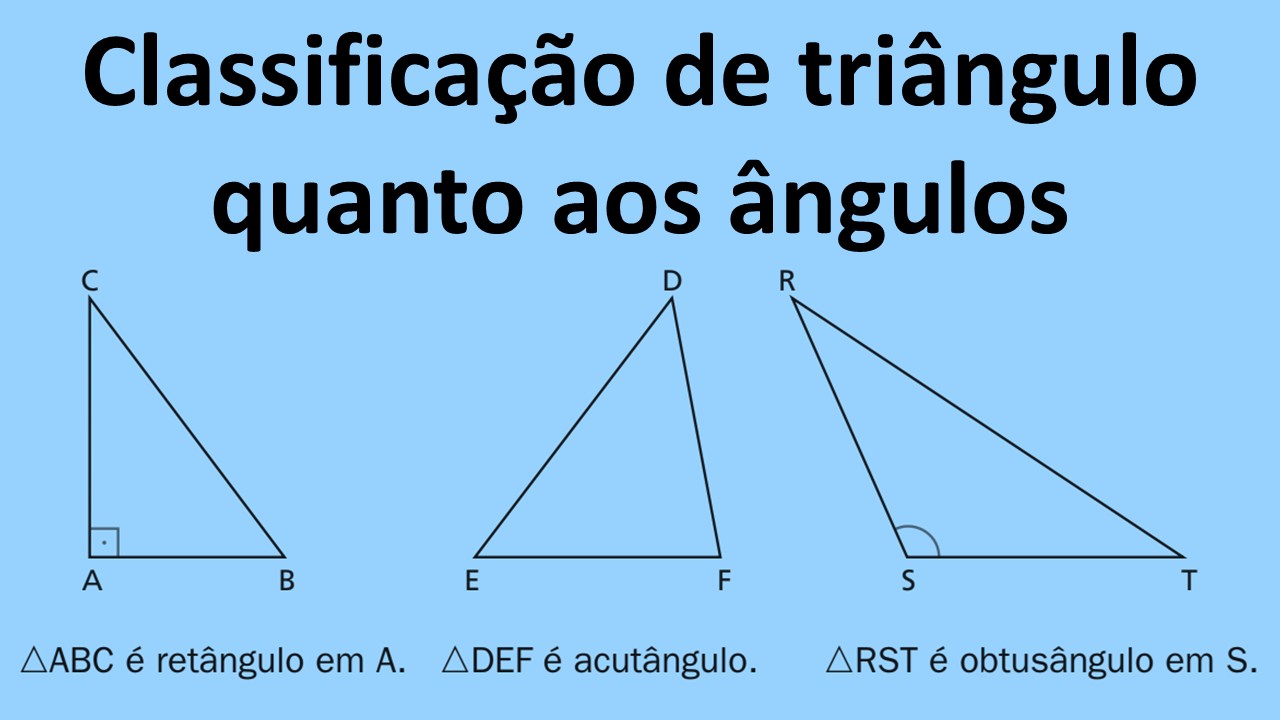
Visão geral (com figuras)

ΔDEF acutângulo: todos os ângulos menores que 90°. — ΔDEF acutângulo: \( \angle D,\angle E,\angle F<90^\circ \).

ΔABC retângulo: ângulo de 90° em A. — ΔABC retângulo: \( \angle A=90^\circ \).

ΔRST obtusângulo: ângulo maior que 90° em S. — ΔRST obtusângulo: \( \angle S>90^\circ \).

O maior ângulo está sempre oposto ao maior lado — regra útil para classificar rapidamente.

Como classificar: por ângulos e por lados (Pitágoras ao contrário)

Para qualquer triângulo com lados \(a,b,c\) (sendo \(c\) o maior) e ângulo oposto \(C\):

Acutângulo ⇔ \(C<90^\circ\) ⇔ \(c^2<a^2+b^2\). Retângulo ⇔ \(C=90^\circ\) ⇔ \(c^2=a^2+b^2\). Obtusângulo ⇔ \(C>90^\circ\) ⇔ \(c^2>a^2+b^2\). Lei dos cossenos: \(c^2=a^2+b^2-2ab\cos C\).

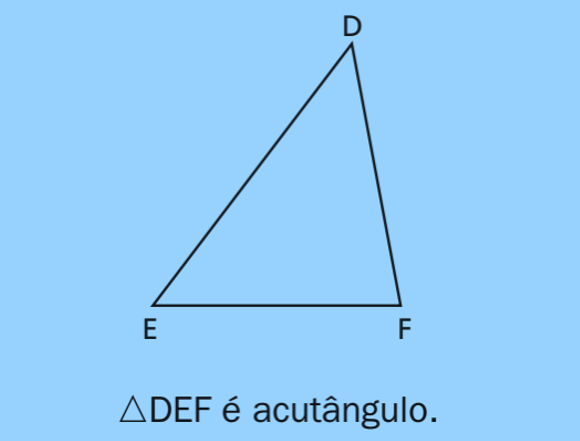
Triângulo Acutângulo — ΔDEF

Triângulo ΔDEF acutângulo: ângulos D, E e F são agudos. — **ΔDEF** com \( \angle D,\angle E,\angle F<90^\circ \).

Em ΔDEF todos os ângulos são agudos. Ortocentro, incentro e circuncentro ficam dentro do triângulo. Alturas são internas. Veja o artigo completo: triângulo acutângulo.

Critério (lados): \(c^2<a^2+b^2\). Área: \(A=\dfrac{ab\sin C}{2}\). Alturas: \(h_a=\dfrac{2A}{a},\; h_b=\dfrac{2A}{b},\; h_c=\dfrac{2A}{c}\). Raios: \(R=\dfrac{c}{2\sin C},\; r=\dfrac{A}{s}\) com \(s=\tfrac{a+b+c}{2}\).

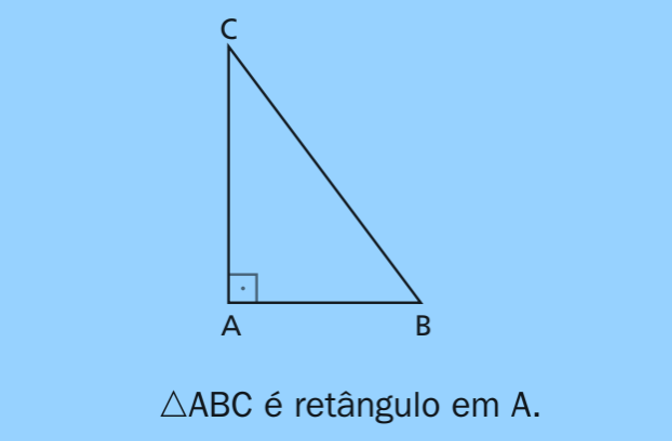
Triângulo Retângulo — ΔABC

Triângulo ΔABC retângulo com ângulo reto em A. — **ΔABC** retângulo em A: \( \angle A=90^\circ \).

Em ΔABC há um ângulo reto. A hipotenusa é o lado oposto a \( \angle A \). Veja: triângulo retângulo.

Pitágoras: \(c^2=a^2+b^2\). Razões trig.: \(\sin\theta=\frac{\text{cat.op.}}{\text{hip.}},\ \cos\theta=\frac{\text{cat.adj.}}{\text{hip.}}\). Área: \(A=\dfrac{\text{cateto}_1\cdot \text{cateto}_2}{2}\). Semelhança com triângulos formados pela altura na hipotenusa.

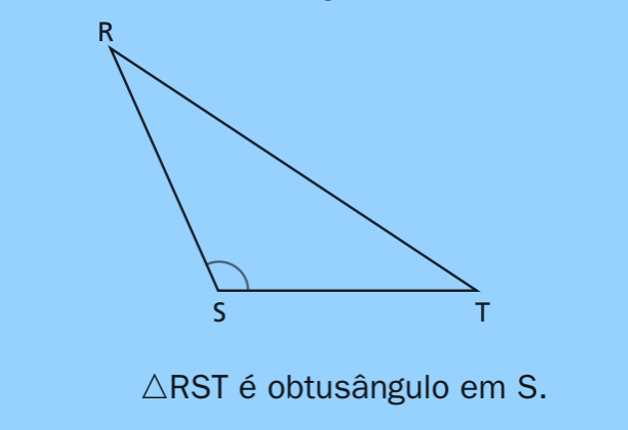
Triângulo Obtusângulo — ΔRST

Triângulo ΔRST obtusângulo: ângulo obtuso em S. — **ΔRST** com \( \angle S>90^\circ \) (obtuso).

Em ΔRST um ângulo é obtuso. Ortocentro e circuncentro ficam fora do triângulo; a altura relativa ao lado oposto ao ângulo obtuso cai na extensão do lado. Veja: triângulo obtusângulo.

Critério (lados): \(c^2>a^2+b^2\). Lei dos cossenos: \(c^2=a^2+b^2-2ab\cos C\) com \(\cos C<0\). Área: \(A=\dfrac{ab\sin C}{2}\). Alturas externas: \(h_b=\dfrac{2A}{b}\) quando o pé cai fora.

Exemplos resolvidos (passo a passo vertical)

Exemplo 1 — Classifique o triângulo de lados \(7,8,9\).

Mostrar solução

Maior lado: \(c=9\).

\(c^2=9^2\)
=81

\(a^2+b^2=7^2+8^2\)
=49+64
=113

Como \(81<113\), é acutângulo (como ΔDEF).

Exemplo 2 — Dados \(a=9\), \(b=12\) e \(C=120^\circ\). Classifique e calcule \(c\).

Mostrar solução

Como \(C=120^\circ>90^\circ\), é obtusângulo (ΔRST).

\(c^2=a^2+b^2-2ab\cos C\)
\(=9^2+12^2-2\cdot 9\cdot 12\cdot \cos120^\circ\)
\(=81+144-216\cdot (-\tfrac12)\)
\(=333\)

\(c=\sqrt{333}\approx 18{,}25\).

Exemplo 3 — Um triângulo tem \(a=5\), \(b=12\), \(c=13\). Classifique-o.

Mostrar solução

\(c^2=13^2=169\)

\(a^2+b^2=25+144=169\)

Como \(c^2=a^2+b^2\), é retângulo (ΔABC).

Exercícios de múltipla escolha

1) Classifique \(6,7,8\).

A) Retângulo B) Obtusângulo C) Acutângulo D) Isósceles E) Equilátero

Mostrar solução

Maior lado \(c=8\).

\(c^2=64\)

\(a^2+b^2=36+49=85\)

Como \(64<85\), Acutângulo.

2) Para \(8,15,c\) (com \(c\) maior), o triângulo é retângulo quando:

A) \(c=15\) B) \(c=16\) C) \(c=17\) D) \(c=18\) E) \(c=20\)

Mostrar solução

\(c^2=8^2+15^2=64+225=289\Rightarrow c=17\). Alternativa C.

Continue estudando

Triângulo acutângulo Triângulo retângulo Triângulo obtusângulo Área de triângulo Pontos notáveis Tipos de triângulos Triângulo equilátero Triângulo escaleno

Classificação de Triângulo quanto aos Ângulos

Classificação de Triângulos quanto aos Ângulos

Visão geral (com figuras)

Como classificar: por ângulos e por lados (Pitágoras ao contrário)

Triângulo Acutângulo — ΔDEF

Triângulo Retângulo — ΔABC

Triângulo Obtusângulo — ΔRST

Exemplos resolvidos (passo a passo vertical)

Exercícios de múltipla escolha

Continue estudando

Classificação de Triângulo quanto aos Lados

Área de Triângulo

Coroa Circular

"Artigo escrito por"

Adriano Rocha

Nos ajude compartilhando esse post 😉

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Triângulo 3 4 5

Triângulo Isósceles

Desigualdade Triangular

Triângulo Escaleno

Área de Triângulo

Triângulo Equilátero

📘 Baixe Grátis o eBook de Fórmulas Matemática

📘 Mapas Mentais

📚 10 E-books de Matemática

Questões

Conteúdo

Banca