Coeficiente Angular da Reta — Fórmula, Definição e Exercícios
O coeficiente angular é um conceito fundamental na geometria analítica e está diretamente relacionado à inclinação de uma reta no plano cartesiano. Ele indica quanto a reta “sobe” ou “desce” quando o valor de \(x\) aumenta, sendo um parâmetro essencial para entender o comportamento gráfico de funções lineares.
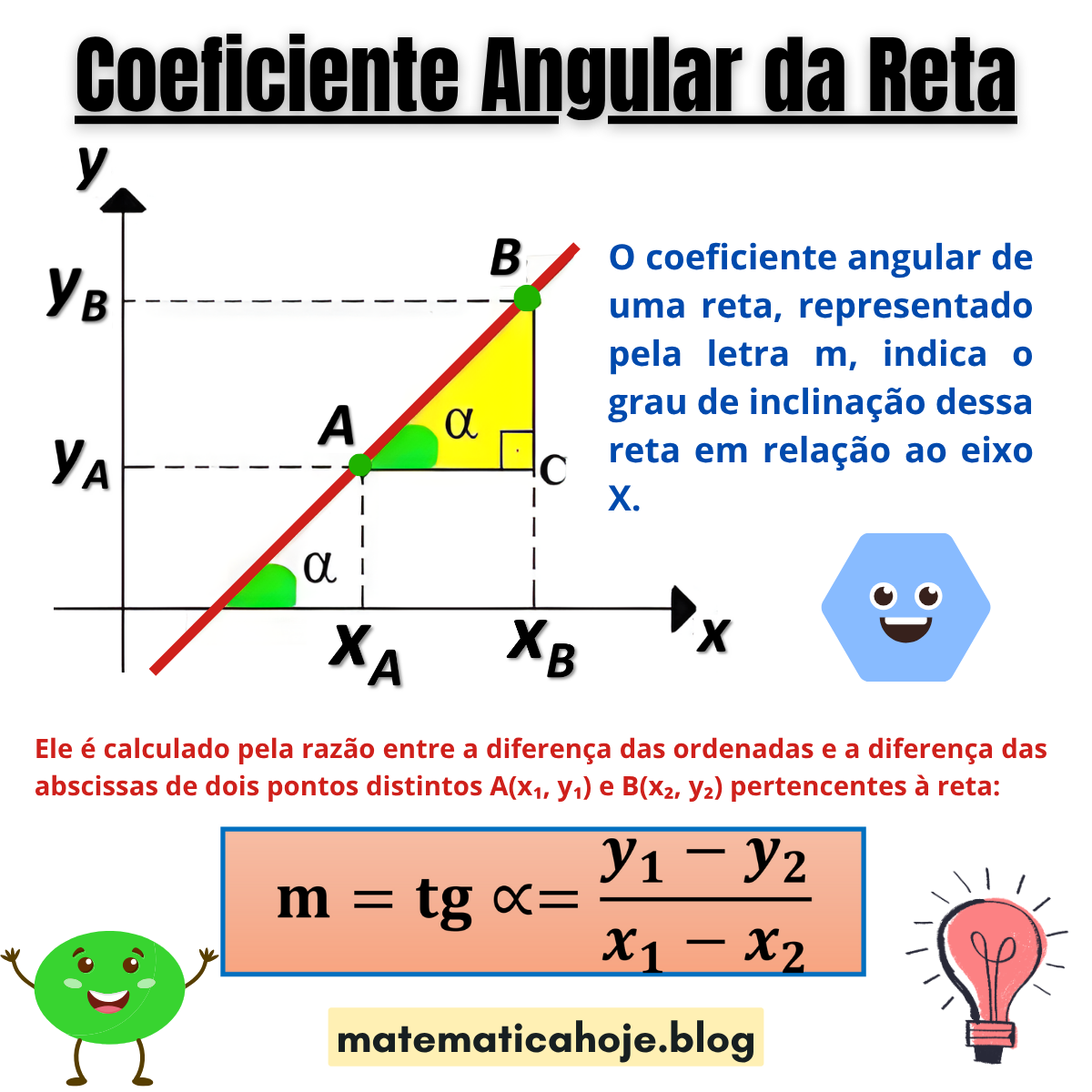
📘 O que é o Coeficiente Angular
O coeficiente angular de uma reta, representado pela letra \( m \), indica o grau de inclinação da reta em relação ao eixo \( X \). Ele mostra o quanto o valor de \( y \) varia quando o valor de \( x \) aumenta uma unidade.
É calculado pela razão entre a diferença das ordenadas e a diferença das abscissas de dois pontos distintos \( A(x_1, y_1) \) e \( B(x_2, y_2) \) pertencentes à reta:
📐 Interpretação Geométrica
O valor de \( m \) define a inclinação da reta:
- Se \( m > 0 \), a reta é crescente — sobe da esquerda para a direita.
- Se \( m < 0 \), a reta é decrescente — desce da esquerda para a direita.
- Se \( m = 0 \), a reta é horizontal.
- Se o denominador \( x_2 – x_1 = 0 \), a reta é vertical e não possui coeficiente angular definido.
🧩 Exemplo Resolvido 1
Exemplo: Determine o coeficiente angular da reta que passa pelos pontos \( A(1, 2) \) e \( B(4, 8) \).
Resolução:
\( m = \dfrac{y_2 – y_1}{x_2 – x_1} = \dfrac{8 – 2}{4 – 1} = \dfrac{6}{3} = 2 \)
Resposta: \( m = 2 \)
🧮 Exemplo Resolvido 2
Calcule o coeficiente angular da reta que passa pelos pontos \( A(-3, 5) \) e \( B(2, -5) \).
Resolução:
\( m = \dfrac{-5 – 5}{2 – (-3)} = \dfrac{-10}{5} = -2 \)
Resposta: \( m = -2 \)
📚 Exercícios de Fixação
1. Encontre o coeficiente angular da reta que passa pelos pontos \( A(2, 3) \) e \( B(6, 9) \).
2. Determine o coeficiente angular da reta que passa pelos pontos \( A(-4, -2) \) e \( B(2, 4) \).
3 (Múltipla escolha). A reta que passa pelos pontos \( A(3, 5) \) e \( B(5, 1) \) possui coeficiente angular:
- A) \( 2 \)
- B) \( -2 \)
- C) \( \dfrac{1}{2} \)
- D) \( -\dfrac{1}{2} \)
🔥 Exercícios Desafiadores
4. (Desafio 1) Determine o coeficiente angular da reta que passa pelos pontos \( A(0, 3) \) e \( B(-4, -1) \).
5. (Desafio 2) Encontre o coeficiente angular da reta que passa pelos pontos \( A(2, -3) \) e \( B(5, -3) \).
6. (Desafio 3) Qual é o coeficiente angular da reta que passa pelos pontos \( A(4, 2) \) e \( B(4, -3) \)?













