Coeficiente Angular (m): como calcular e interpretar
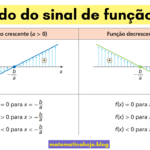
O coeficiente angular (ou inclinação) de uma reta mede quanto a altura muda quando avançamos uma unidade na horizontal. Em função do 1º grau \(f(x)=ax+b\), o coeficiente angular é simplesmente m = a. Ele controla se a reta é crescente, decrescente ou horizontal.
Fórmulas essenciais
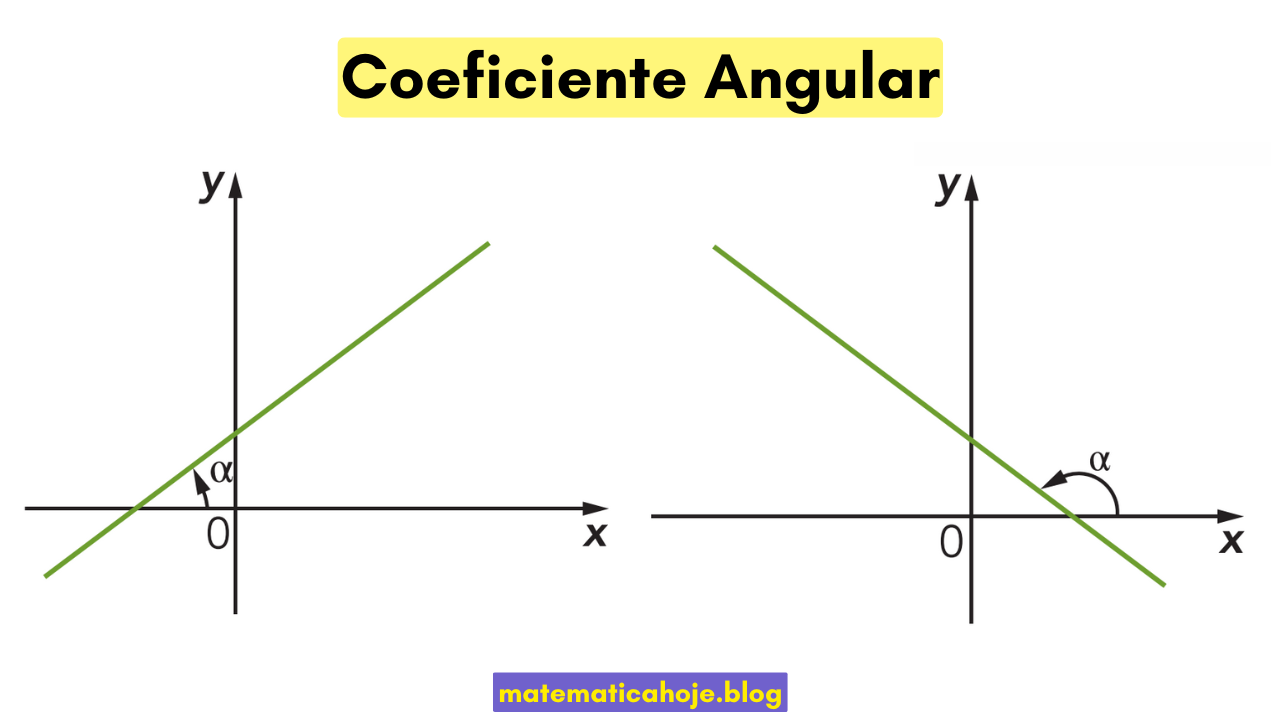
- Sinal: \(m\gt 0\) → reta crescente; \(m\lt 0\) → decrescente; \(m=0\) → constante.
- Interpretação: “A cada \(1\) em \(x\), \(y\) varia \(m\)”. Ex.: \(m=2\) significa “sobe 2 para a direita 1”.
- Unidade: \([\text{y}]/[\text{x}]\) (ex.: km/h, R$/un.).
Como encontrar \(m\) na prática
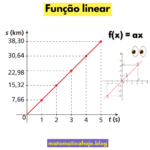
- Pela lei da função: em \(f(x)=ax+b\), leia \(m=a\). Veja também função linear (\(b=0\)).
- No gráfico: escolha dois pontos da reta, calcule \(\Delta y/\Delta x\). Dica: use o quadriculado para contar “sobe/desce” e “anda”.
- Pelo ângulo: meça \(\alpha\) desde o semieixo \(x\) positivo até a reta (no sentido anti-horário) e aplique \(m=\tan\alpha\).
Para traçar a reta com rapidez, combine \(m\) com o intercepto em \(y\) \(b\): marque \(B=(0,b)\), avance \(\Delta x\) e suba/ desça \(\Delta y=m\Delta x\). Tutorial completo em como construir o gráfico da função afim.
📘 Precisa das fórmulas sempre à mão?
Baixe o eBook Fórmulas Matemática com resumos práticos de funções, gráficos, trigonometria e muito mais. Ideal para revisões rápidas.
Baixar eBook de FórmulasExemplos resolvidos
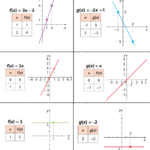
Exemplo 1 — A partir da equação. Dada \(f(x)=3x-2\): determine \(m\), classifique a reta e estime o ângulo \(\alpha\).
Ver solução
Em \(f(x)=ax+b\), \(m=a=3\) ⇒ reta crescente. \(\alpha=\arctan(3)\approx 71{,}6^\circ\).
Exemplo 2 — Usando dois pontos. Uma reta passa por \(A(-3,2)\) e \(B(5,-6)\). Encontre \(m\) e a lei \(f(x)\).
Ver solução
\(m=\dfrac{-6-2}{5-(-3)}=\dfrac{-8}{8}=-1\). Como \(y=mx+b\), substitua \(A\): \(2=(-1)(-3)+b\Rightarrow b=-1\). Logo \(f(x)=-x-1\) (reta decrescente).
Exemplo 3 — Pelo ângulo e intercepto. A reta faz \(\alpha=30^\circ\) com o eixo \(x\) e corta \(y\) em \(b=2\). Determine \(f(x)\) e o zero.
Ver solução
\(m=\tan 30^\circ=\sqrt{3}/3\approx0{,}577\). Logo \(f(x)=0{,}577x+2\). Zero \(x_0=-b/m\approx -2/0{,}577\approx -3{,}46\). Veja zero da função.
Exercícios propostos (com gabarito)
1) Ache o coeficiente angular da reta que passa por \(P(2,5)\) e \(Q(11, -4)\). Classifique a reta e estime \(\alpha\) (graus, uma casa).
Gabarito
\(m=\dfrac{-4-5}{11-2}=\dfrac{-9}{9}=-1\) (decrescente). \(\alpha=\arctan(-1)=-45^\circ\) (ou \(135^\circ\)).
2) Uma reta tem intercepto \(b=-3\) e ângulo \(\alpha=135^\circ\). Escreva a função e informe o zero.
Gabarito
\(\tan 135^\circ=-1\Rightarrow m=-1\). \(f(x)=-x-3\). Zero \(x_0=-b/m=-(-3)/(-1)=-3\).
3) Complete a tabela e determine \(m\).
| \(x\) | 0 | 2 | 5 |
|---|---|---|---|
| \(f(x)\) | 4 | 10 | ? |
Gabarito
De 0→2: \(\Delta y=6\Rightarrow m=6/2=3\). Logo \(f(x)=3x+4\); portanto \(f(5)=19\).
4) Uma estrada sobe \(8\) m a cada \(200\) m na horizontal. Modele a inclinação como coeficiente angular (em m/m e em %).
Gabarito
\(m=\dfrac{8}{200}=0{,}04\ \text{m/m}\). Em porcentagem, 4% (rampa de 4%).
5) Determine \(m\) observando o gráfico: a reta desce 2 unidades em \(y\) quando avança 5 em \(x\) e corta \(y\) em \(b=1\). Escreva \(f(x)\).
Gabarito
\(m=\Delta y/\Delta x=-2/5=-0{,}4\). Assim, \(f(x)=-0{,}4x+1\) (decrescente). Interseção das retas? Veja interseção de retas.