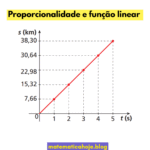
Coeficiente linear (b): o “ponto de partida” da reta
Em toda função do 1º grau \(f(x)=ax+b\), o número \(b\) é o coeficiente linear (ou termo independente). Ele indica onde a reta corta o eixo \(y\) e, portanto, define a altura inicial da função. Para dominar gráficos e problemas do ENEM, combine este estudo com: coeficiente angular, construção do gráfico, zero da função, interseção de retas e estudo do sinal.
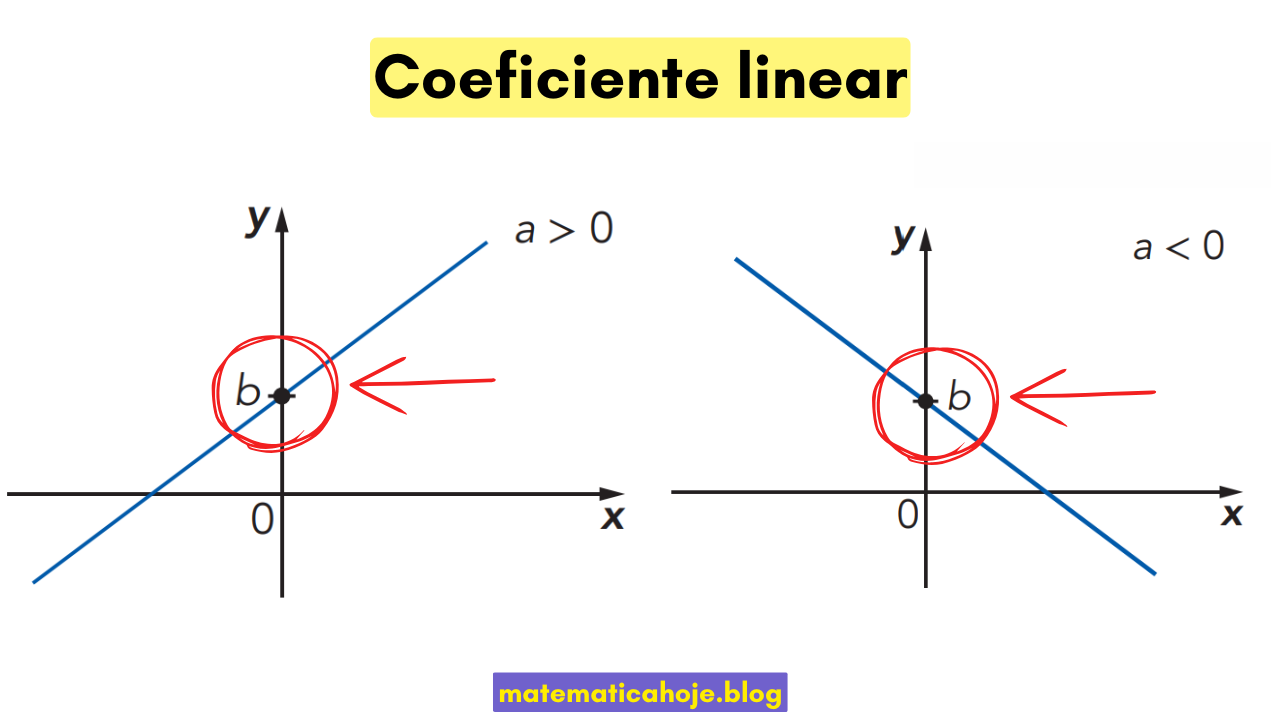
Definição e leitura no gráfico
- Tradução vertical: \(b\) “sobe” ou “desce” a reta sem mudar a inclinação.
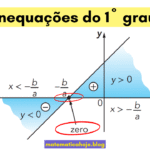
- Sinal de \(b\): \(b\gt 0\) → corta o eixo \(y\) acima da origem; \(b\lt 0\) → abaixo; \(b=0\) → passa pela origem (caso função linear).
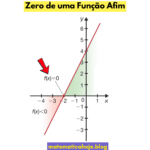
- Relação com o zero: para \(a\ne 0\), \(x_0=-\dfrac{b}{a}\) (ponto onde \(f(x)=0\)).
- Casos-limite: se \(a=0\), \(f(x)=b\) é função constante (reta horizontal em \(y=b\)).
Como encontrar \(b\) em cada situação
- Pela lei \(f(x)=ax+b\): leia diretamente \(b\).
- A partir do gráfico: identifique o ponto em que a reta cruza o eixo \(y\). A ordenada desse ponto é \(b\).
- Com dois pontos e o coeficiente angular: primeiro calcule \(a=\dfrac{y_2-y_1}{x_2-x_1}\) e depois use \(b=y-ax\) substituindo qualquer ponto da reta.
- Com tabela: se a tabela trouxer \(x=0\), então \(b=f(0)\). Se não trouxer, determine \(a\) e use \(b=y-ax\).
📘 Fórmulas sempre à mão
Baixe o eBook Fórmulas Matemática com resumos de funções, gráficos, trigonometria e muito mais — perfeito para revisões antes das provas.
Baixar eBook de FórmulasExemplos resolvidos
Exemplo 1 — Lendo \(b\) na lei. Para \(f(x)=2x-3\), identifique \(b\), o ponto \(B\) e o zero \(x_0\). Classifique a posição do intercepto.
Ver solução
\(b=-3\Rightarrow B=(0,-3)\) (abaixo da origem). Zero \(x_0=-(-3)/2=1{,}5\). A reta cruza \(y\) em \(-3\) e \(x\) em \(1{,}5\).
Exemplo 2 — Com dois pontos. A reta passa por \(A(3,1)\) e \(B(7,9)\). Encontre \(a\) e \(b\), escrevendo \(f(x)\).
Ver solução
\(a=\dfrac{9-1}{7-3}=2\). Substituindo em \(b=y-ax\) com \(A\): \(b=1-2\cdot3=-5\). Logo \(f(x)=2x-5\) e \(B=(0,-5)\).
Exemplo 3 — Contexto real (custo com taxa fixa). Uma corrida de app custa \(C(t)=0{,}80\,t+3\) (R$), em que \(t\) está em minutos. Interprete \(b\) e estime o tempo para que o custo atinja R$ 11,40.
Ver solução
O \(b=3\) é a tarifa inicial (taxa fixa). Resolva \(0{,}80\,t+3=11{,}40\Rightarrow t=10{,}5\ \text{min}\).
Exemplo 4 — Pelo gráfico. Uma reta cruza o eixo \(y\) em \(y=4\) e desce \(3\) unidades quando avança \(2\) (ou seja, \(a=-3/2\)). Escreva \(f(x)\) e encontre o zero.
Ver solução
\(b=4\) e \(a=-\frac{3}{2}\Rightarrow f(x)=-\frac{3}{2}x+4\). Zero \(x_0=-b/a=-4/(-3/2)=\frac{8}{3}\approx2{,}67\). Relembre zero da função.
Erros comuns
- Confundir \(b\) com o zero. Zero é em \(x\) (\(x_0=-b/a\)); \(b\) é em \(y\) (\(B=(0,b)\)).
- Tentar “ver” \(b\) em tabela sem \(x=0\). Nestes casos, calcule \(a\) e use \(b=y-ax\).
- Esquecer que mudar \(b\) move a reta na vertical, mas não altera a inclinação (que depende de \(a\)).
Exercícios propostos (com gabarito)
1) Numa assinatura de streaming, o custo mensal é \(C(n)=12\,n+19{,}90\), em que \(n\) é o número de pacotes extras. Interprete \(b\) e calcule \(C\) para \(n=3\).
Gabarito
\(b=19{,}90\) é a taxa fixa mensal sem extras. \(C(3)=12\cdot3+19{,}90=55{,}90\) (R$).
2) A reta tem inclinação \(a=1{,}5\) e passa por \(P(4,1)\). Determine \(b\), a função e o zero.
Gabarito
\(b=y-ax=1-1{,}5\cdot4=-5\). \(f(x)=1{,}5x-5\). Zero \(x_0=-b/a=5/1{,}5\approx3{,}33\).
3) Complete e ache \(b\):
| \(x\) | 0 | 1 | 2 |
|---|---|---|---|
| \(f(x)\) | ? | 7 | 10 |
Gabarito
De 1→2, \(\Delta y=3\Rightarrow a=3\). Então \(b=f(1)-a\cdot1=7-3=4\). Logo \(f(0)=b=4\).
4) Uma reta tem zero em \(x=5\) e coeficiente angular \(a=-\dfrac{2}{5}\). Encontre \(b\) e escreva a lei.
Gabarito
Zero \(x_0=-b/a=5\Rightarrow b=-5a= -5\cdot(-2/5)=2\). \(f(x)=-\dfrac{2}{5}x+2\).
5) O gráfico de uma função é uma reta horizontal que passa por \(y=-3\). Identifique \(a\) e \(b\) e diga se há zero.
Gabarito
\(a=0\), \(b=-3\) ⇒ função constante \(f(x)=-3\). Não possui zero (não cruza \(x\)).