Questão 6. Esboce, no sistema cartesiano, o gráfico de cada função quadrática definida a seguir:
- a) \( y = -x^2 \)
- b) \( y = x^2 – 4 \)
- c) \( y = -x^2 + 6x – 9 \)
- d) \( y = x^2 – 5x \)
Ver solução completa
Letra a) \( y = -x^2 \)
Coeficientes: \( a = -1 \), \( b = 0 \), \( c = 0 \)
Vértice: \( x_v = -\frac{b}{2a} = 0 \) ⇒ \( y_v = 0 \)
Raízes: \( y = 0 \Rightarrow -x^2 = 0 \Rightarrow x = 0 \)
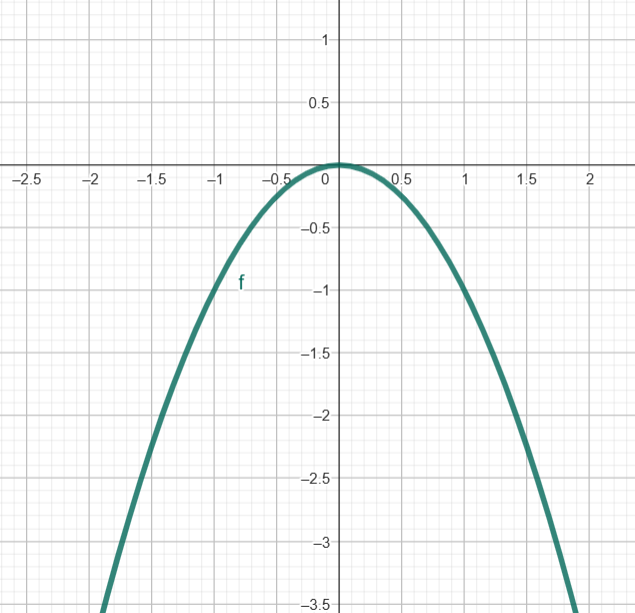
Letra b) \( y = x^2 – 4 \)
Coeficientes: \( a = 1 \), \( b = 0 \), \( c = -4 \)
Vértice: \( x_v = 0 \) ⇒ \( y_v = -4 \)
Raízes: \( x^2 – 4 = 0 \Rightarrow x = \pm 2 \)
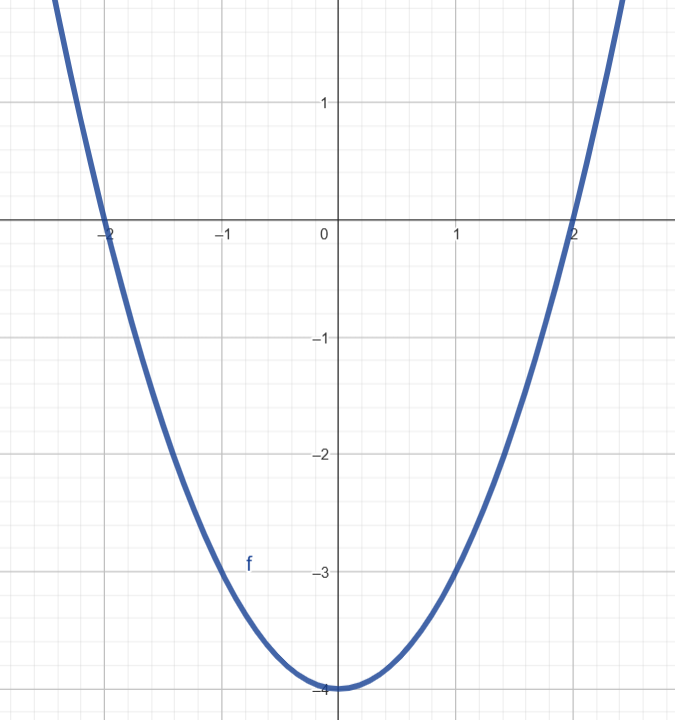
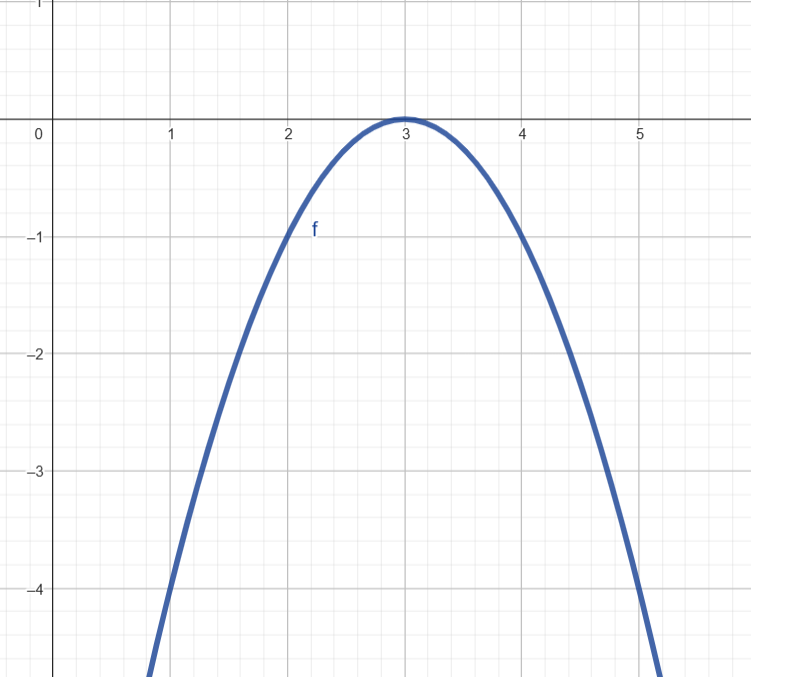
Letra c) \( y = -x^2 + 6x – 9 \)
Coeficientes: \( a = -1 \), \( b = 6 \), \( c = -9 \)
Vértice: \( x_v = -\frac{6}{2 \cdot (-1)} = 3 \)
\( y_v = -3^2 + 6\cdot3 – 9 = -9 + 18 – 9 = 0 \)
Raízes: \( x^2 – 6x + 9 = 0 \Rightarrow (x – 3)^2 = 0 \Rightarrow x = 3 \) (raiz dupla)
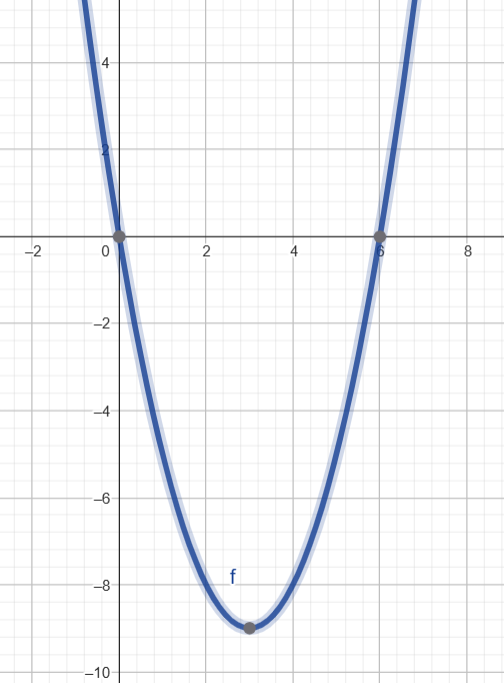
Letra d) \( y = x^2 – 5x \)
Coeficientes: \( a = 1 \), \( b = -5 \), \( c = 0 \)
Vértice: \( x_v = -\frac{-5}{2\cdot1} = \frac{5}{2} \)
\( y_v = \left(\frac{5}{2}\right)^2 – 5\cdot\frac{5}{2} = \frac{25}{4} – \frac{25}{2} = \frac{25 – 50}{4} = \frac{-25}{4} \)
Raízes: \( x(x – 5) = 0 \Rightarrow x = 0 \) ou \( x = 5 \)