Construção do Gráfico da Função Afim
Aqui você encontra um guia reformulado e direto para traçar o gráfico de \(f(x)=ax+b\). O conteúdo segue o padrão visual da imagem e cobre 6 padrões clássicos (incluindo funções constantes), com exemplos e exercícios no final. Ideal para ENEM, vestibulares e concursos.
1) Conceitos-chave
- Coeficiente angular \(a\): inclinação (sobe se \(a>0\), desce se \(a<0\)).
- Coeficiente linear \(b\): valor quando \(x=0\) (intercepto em \(y\)).
- Zero da função: \(x_0=-\dfrac{b}{a}\) (intercepto em \(x\)).
2) Três rotas para traçar a reta
2.1) Interceptos (método mais rápido)
- Ponto \(A\) no eixo \(y\): \(A=(0,b)\).
- Ponto \(B\) no eixo \(x\): \(B=(x_0,0)\), com \(x_0=-\dfrac{b}{a}\).
- Trace a reta \(\overline{AB}\).
2.2) Tabela de valores
Escolha dois \(x\), calcule \(f(x)\) e una os pontos.
2.3) Inclinação
Use \(a=\dfrac{\Delta y}{\Delta x}\): a partir de um ponto conhecido, avance \(\Delta x\) e suba/ desça \(\Delta y\).
📘 Dica de estudo
Tenha as principais fórmulas em mãos com o eBook Fórmulas Matemática — perfeito para revisão antes da prova.
Baixar eBook de Fórmulas3) Os 6 padrões da imagem (com exemplos)
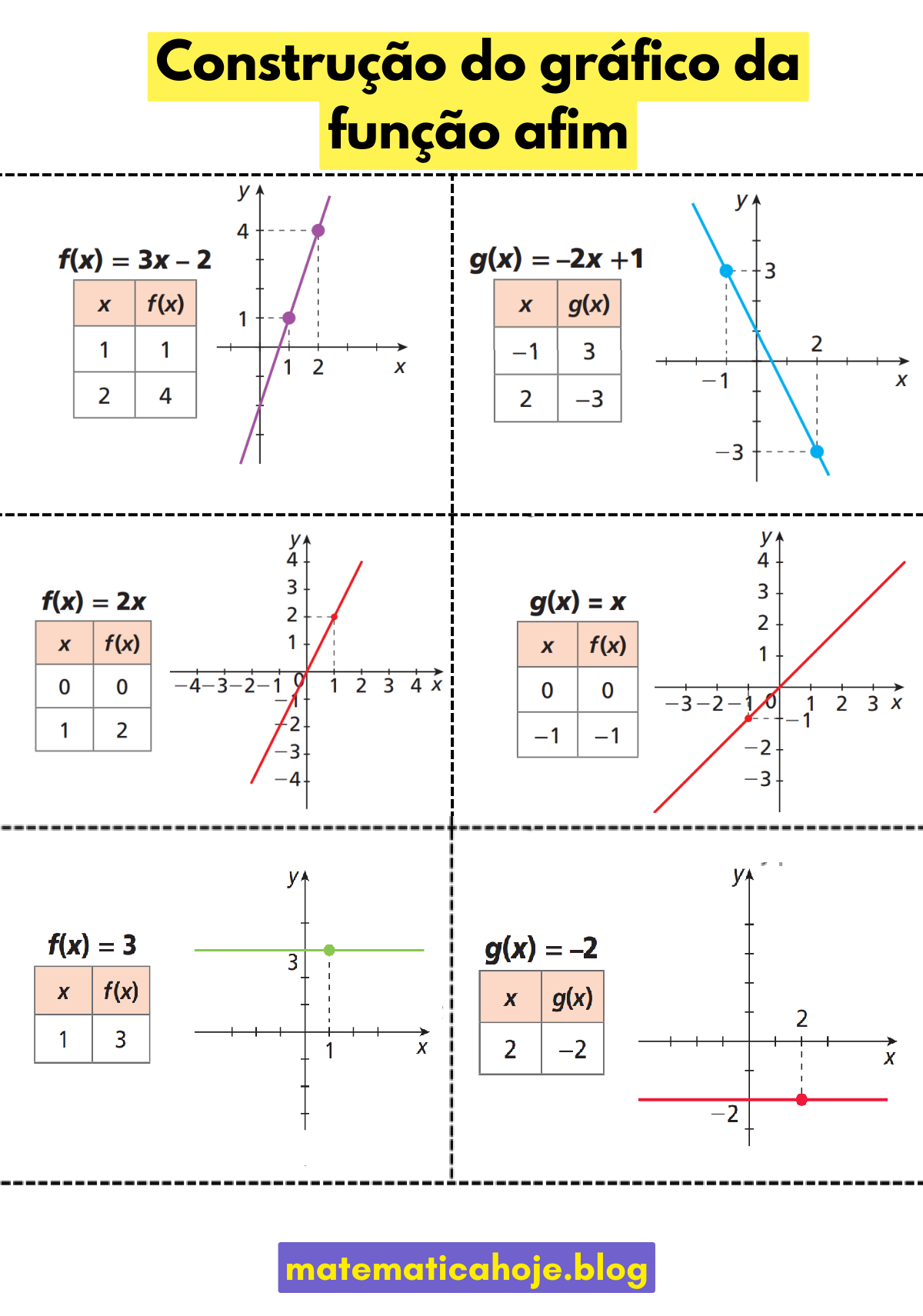
Padrão A — Reta crescente com \(b\) positivo
Exemplo: \(f(x)=3x-2\). Construa com tabela e confirme pelos interceptos.
Ver solução
| \(x\) | \(f(x)\) |
|---|---|
| 1 | 1 |
| 2 | 4 |
Interceptos: \(A=(0,-2)\), \(x_0=\tfrac{2}{3}\). Reta crescente (a=3).
Padrão B — Reta decrescente com \(b\) positivo
Exemplo: \(g(x)=-2x+1\). Use tabela e o zero.
Ver solução
| \(x\) | \(g(x)\) |
|---|---|
| \(-1\) | 3 |
| 2 | \(-3\) |
Interceptos: \(A=(0,1)\), \(x_0=\tfrac{1}{2}\). Reta decrescente (a=-2).
Padrão C — Reta que passa pela origem (multiplicativa)
Exemplo: \(f(x)=2x\). Parta de \((0,0)\) e aplique a inclinação \(2=\dfrac{\Delta y}{\Delta x}\).
Ver solução
De \((0,0)\), com \(\Delta x=1\) ⇒ \(\Delta y=2\) ⇒ ponto \((1,2)\). Reta crescente.
Padrão D — Reta \(45^\circ\) (inclinação 1)
Exemplo: \(g(x)=x\). Subida 1 para avanço 1.
Padrão E — Função constante acima do eixo \(x\)
Exemplo: \(f(x)=3\). Reta horizontal em \(y=3\).
Padrão F — Função constante abaixo do eixo \(x\)
Exemplo: \(g(x)=-2\). Reta horizontal em \(y=-2\).
4) Checklist rápido
- Já tem dois pontos? (interceptos, tabela ou inclinação).
- Confirmou o sinal de \(a\) (sobe/ desce)?
- Marcou escala coerente nos eixos?
5) Exercícios propostos (com soluções)
1) Construa o gráfico de \(h(x)=4x-5\) pelos interceptos e indique se a reta é crescente ou decrescente.
Ver solução
\(A=(0,-5)\); \(x_0=\frac{5}{4}=1{,}25\). Como \(a=4>0\), reta crescente.
2) Usando o método da inclinação, trace \(p(x)=-\tfrac{3}{2}x+4\) a partir do ponto em \(y\).
Ver solução
Comece em \((0,4)\). Para \(\Delta x=2\), \(\Delta y=-3\) ⇒ ponto \((2,1)\). Zero: \(x_0=\dfrac{8}{3}\).
3) Determine a função da reta que passa por \(A(1,4)\) e \(B(3,8)\) e esboce seu gráfico.
Ver solução
\(a=\dfrac{8-4}{3-1}=2\); \(b=4-2\cdot1=2\). Logo \(f(x)=2x+2\). Interceptos: \((0,2)\) e \(x_0=-1\).
4) Esboce os gráficos e encontre a interseção de \(y=1{,}5x-3\) e \(y=-0{,}5x+1\).
Ver solução
Igualando: \(1{,}5x-3=-0{,}5x+1 \Rightarrow 2x=4 \Rightarrow x=2\); \(y=0\). Ponto \((2,0)\).
5) Um serviço cobra \(C(d)=5+2{,}2d\) (R$) para distância \(d\) em km. Represente no intervalo \(0\le d\le 6\) e calcule \(C(3)\).
Ver solução
Reta com \((0,5)\) e \((6,18{,}2)\). \(C(3)=11{,}6\) reais.
6) Classifique e esboce: \(y=2x+1\) e \(y=2x-3\).
Ver solução
Mesma inclinação ⇒ paralelas. Sem interseção.