Coroa Circular (Anel Circular)

A coroa circular é a região entre duas circunferências concêntricas (mesmo centro) de raios \(R\) e \(r\) \((R>r)\). Também é chamada de anel circular. Veja as fórmulas essenciais, um exemplo resolvido passo a passo e exercícios.

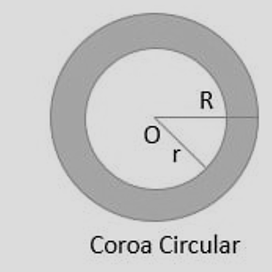
Coroa circular (anel) com raios R e r — Região em azul entre os círculos de raios \(R\) (externo) e \(r\) (interno).

Estude junto com: Circunferência e Círculo, Área do Círculo, Comprimento da Circunferência e Área do Setor Circular.

Definição e elementos

R: raio externo; r: raio interno (\(R>r\)).
t: espessura do anel, \(t=R-r\).
r_m: raio médio, \(r_m=\dfrac{R+r}{2}\).

Fórmulas essenciais (empilhadas)

\[ \textbf{Área da coroa:}\quad \boxed{A_{\text{coroa}}=\pi(R^2-r^2)} \]

\[ \textbf{Expressão pela espessura }(t=R-r):\quad A_{\text{coroa}}=\pi\big((r+t)^2-r^2\big)=\boxed{2\pi r t+\pi t^2} \]

Nota: aqui \(r\) é o raio interno. Se \(t\) for pequeno frente a \(r\), a parcela \(\pi t^2\) é pequena: \(A\approx 2\pi r\,t\).

\[ \textbf{Fórmula do raio médio (exata):}\quad \boxed{A_{\text{coroa}}=2\pi\,r_m\,t}\quad \text{com}\ r_m=\dfrac{R+r}{2},\ t=R-r \]

Interpretação geométrica: área do “retângulo” formado pelo comprimento médio \(2\pi r_m\) e espessura \(t\).

\[ \textbf{Circunferências de contorno:}\quad C_{\text{ext}}=2\pi R,\quad C_{\text{int}}=2\pi r \]

Exemplo resolvido (passo a passo)

1) Área da coroa a partir de \(R\) e \(r\)

Um anel metálico tem raios \(R=20\,\text{cm}\) e \(r=14\,\text{cm}\). Calcule a área da coroa circular.

Ver solução

\[ \begin{aligned} A_{\text{coroa}}&=\pi(R^2-r^2)\\ &=\pi\,(20^2-14^2)\\ &=\pi\,(400-196)\\ &=\pi\cdot 204\\ &\approx \boxed{641{,}52\ \text{cm}^2} \end{aligned} \]

Exercícios resolvidos

(E1) Encontrar \(r\) conhecendo a área e \(R\)

Uma moldura circular tem área \(A=200\pi\,\text{cm}^2\) e raio externo \(R=15\,\text{cm}\). Encontre o raio interno \(r\).

Mostrar solução

\[ \begin{aligned} A_{\text{coroa}}&=\pi(R^2-r^2)\\ 200\pi&=\pi(15^2-r^2)\\ 200&=225-r^2\\ r^2&=25\\ r&=\boxed{5\ \text{cm}} \end{aligned} \]

(E2) Usando a espessura \(t\)

Uma pista circular tem miolo interno de raio \(r=30\,\text{m}\). A faixa de corrida tem espessura uniforme \(t=1{,}2\,\text{m}\). Calcule a área da faixa.

Mostrar solução

\[ \begin{aligned} A_{\text{coroa}}&=2\pi r t+\pi t^2\\ &=2\pi\cdot 30\cdot 1{,}2+\pi\cdot (1{,}2)^2\\ &=72\pi+\ 1{,}44\pi\\ &=73{,}44\pi\\ &\approx \boxed{230{,}72\ \text{m}^2} \end{aligned} \]

(E3) Pela fórmula do raio médio

Uma arruela possui \(R=8\,\text{cm}\) e \(r=6\,\text{cm}\). Use \(r_m\) e \(t\) para calcular a área.

Mostrar solução

\[ \begin{aligned} r_m&=\frac{R+r}{2}=\frac{8+6}{2}=7\ \text{cm}\\ t&=R-r=8-6=2\ \text{cm}\\[6pt] A_{\text{coroa}}&=2\pi r_m t\\ &=2\pi\cdot 7\cdot 2\\ &=\boxed{28\pi\ \text{cm}^2\ \ (\approx 87{,}96)} \end{aligned} \]

Erros comuns (e como evitar)

Confundir diâmetro com raio. Se o enunciado der \(D\), lembre que \(R=\dfrac{D}{2}\).
Esquecer a unidade de área. Se os raios estão em cm, a área sai em cm².
Ignorar a parcela \(\pi t^2\). Para anéis muito finos \(t\ll r\), \(A\approx 2\pi r t\). Caso contrário, use a fórmula completa.