O Corolário Inverso do Teorema de Tales é um resultado que funciona como um critério de paralelismo em triângulos. Em vez de começar com um segmento paralelo e concluir que há proporcionalidade, fazemos o caminho inverso: se as razões entre os segmentos forem proporcionais, então o segmento que une os pontos é paralelo a um lado do triângulo.
Figura do Corolário Inverso de Tales
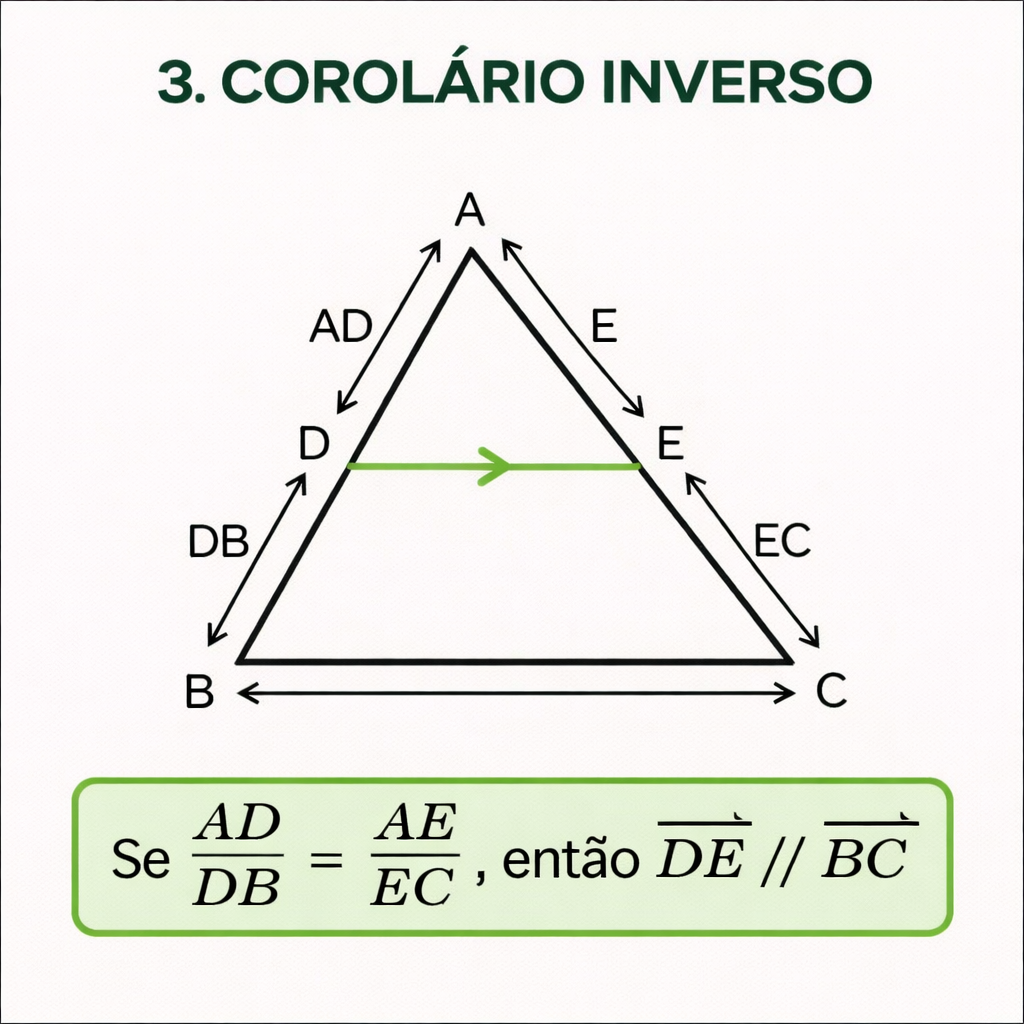
Na figura, temos o triângulo \(ABC\). O ponto \(D\) pertence ao lado \(AB\) e o ponto \(E\) pertence ao lado \(AC\). Os segmentos são indicados por:
- \(AD\) e \(DB\) no lado \(AB\);
- \(AE\) e \(EC\) no lado \(AC\).
Enunciado do Corolário Inverso de Tales
O corolário inverso pode ser enunciado assim:
Se os pontos \(D\) e \(E\) pertencem, respectivamente, aos lados \(AB\) e \(AC\) de um triângulo \(ABC\), e
\(\displaystyle \frac{AD}{DB} = \frac{AE}{EC}\),
então o segmento \(DE\) é paralelo ao lado \(BC\).
Esse resultado é exatamente o “caminho de volta” do Corolário do Teorema de Tales. No corolário direto, partimos do paralelismo para concluir a proporcionalidade; aqui, partimos da proporcionalidade para concluir o paralelismo.
Interpretação geométrica
Quando a razão entre os segmentos de um lado do triângulo é igual à razão entre os segmentos do outro lado, estamos garantindo que existe um segmento \(DE\) que “se comporta” como se fosse obtido pelo Teorema de Tales tradicional.
Ou seja, se:
\(\displaystyle \frac{AD}{DB} = \frac{AE}{EC}\),
então o triângulo \(ADE\) é semelhante ao triângulo \(ABC\), e isso só é possível se \(DE\) for paralelo a \(BC\).
Exemplo resolvido
Problema: No triângulo \(ABC\), os pontos \(D\) e \(E\) pertencem a \(AB\) e \(AC\), respectivamente. Sabemos que \(AD = 4\), \(DB = 6\) e \(AE = 5\). Qual deve ser o valor de \(EC\) para que \(DE\) seja paralelo a \(BC\)?
Para que \(DE\parallel BC\), é necessário que:
\(\displaystyle \frac{AD}{DB} = \frac{AE}{EC}\)
Substituindo os valores conhecidos:
\(\displaystyle \frac{4}{6} = \frac{5}{EC}\)
Aplicando o produto em cruz:
\(4 \cdot EC = 6 \cdot 5 \Rightarrow 4\,EC = 30\)
Isolando \(EC\):
\(EC = \dfrac{30}{4} = \dfrac{15}{2} = 7{,}5\)
Resposta: \(EC = 7{,}5\). Com esse valor, a razão \(\dfrac{AD}{DB}\) é igual à razão \(\dfrac{AE}{EC}\) e, portanto, o segmento \(DE\) será paralelo a \(BC\).
Exercícios para praticar
- No triângulo \(ABC\), \(D\in AB\) e \(E\in AC\). Se \(AD = 3\), \(DB = 9\), \(AE = 2\) e \(EC = 6\), verifique se \(DE\) é paralelo a \(BC\).
- Em um triângulo, temos \(AD = 5\), \(DB = 15\) e \(AE = 4\). Determine o valor de \(EC\) de modo que \(DE\parallel BC\).
- Explique, em palavras, por que a igualdade \[ \frac{AD}{DB} = \frac{AE}{EC} \] garante que o triângulo \(ADE\) é semelhante ao triângulo \(ABC\).
Dica: lembre-se de que o Corolário Inverso de Tales é uma forma de verificar o paralelismo usando apenas razões de segmentos.
Conexões com outros resultados de Tales
O Corolário Inverso de Tales se encaixa em um “pacote” de resultados que aparecem juntos em provas:
Dominar esses quatro resultados deixa a parte de Geometria Plana muito mais leve, principalmente em questões de ENEM, de concursos FGV e de provas militares.
Fortaleça sua base em Geometria
Você pode aprofundar esse conteúdo e revisar toda a Geometria com os materiais do Matemática Hoje:
- Acesse as Questões Resolvidas de Matemática do ENEM
- Baixe os 10 eBooks de Matemática e tenha um material completo de estudo
- Veja o Curso Matemática Básica: Do Zero à Confiança Prática
Continue estudando no Matemática Hoje
- Mapas Mentais de Matemática
- FGV 2025 – Matemática para Concurso
- Entre no grupo gratuito de Matemática no WhatsApp e receba questões diárias.