Crescimento Exponencial

Crescimento Exponencial: conceito, exemplos e aplicações

Crescimento Exponencial

Saiba como funciona o crescimento exponencial, veja exemplos de divisões celulares e descubra aplicações no cotidiano.

Definição: O crescimento exponencial ocorre quando a taxa de crescimento de uma quantidade é proporcional ao seu valor atual. Em outras palavras, quanto mais cresce, mais rapidamente continua a crescer.

1) O conceito matemático

O crescimento exponencial pode ser descrito pela fórmula:

\[ P(t) = P_0 \cdot a^t \] Onde: $P(t)$ = quantidade no tempo $t$ $P_0$ = quantidade inicial $a$ = taxa de crescimento (base) $t$ = tempo ou número de períodos

Se $a > 1$, a quantidade cresce rapidamente. Esse comportamento é comum em populações de bactérias, células ou até no crescimento de juros compostos.

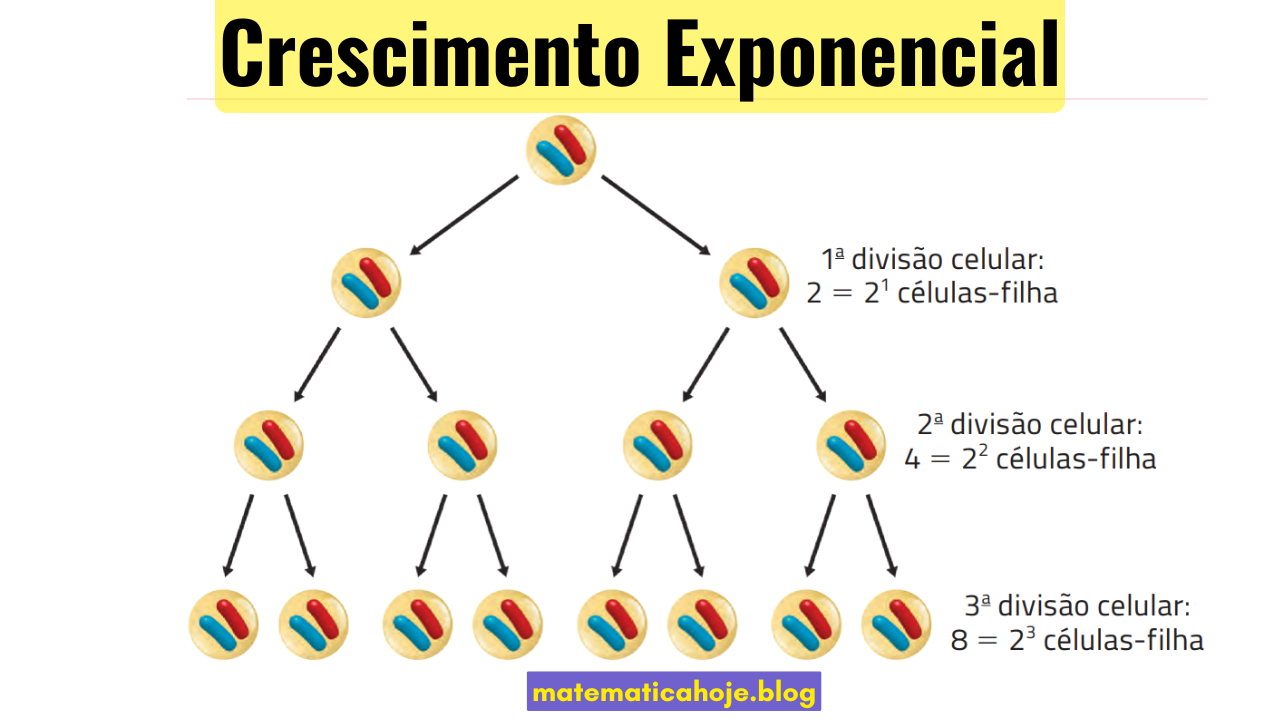
2) Exemplo biológico: divisão celular

– 1ª divisão: $2 = 2^1$ células-filha – 2ª divisão: $4 = 2^2$ células-filha – 3ª divisão: $8 = 2^3$ células-filha – 4ª divisão: $16 = 2^4$ células-filha

Note que o número de células dobra a cada divisão, caracterizando o crescimento exponencial.

3) Crescimento exponencial vs. crescimento linear

No crescimento linear, os valores aumentam de maneira constante (ex.: somando sempre o mesmo número). Já no crescimento exponencial, os valores aumentam em proporções cada vez maiores, o que leva a um crescimento muito mais rápido.

4) Exemplos no cotidiano

População bacteriana em ambientes favoráveis.
Investimentos com juros compostos.
Disseminação de informações nas redes sociais.
Propagação de vírus em epidemias.

5) Exercícios resolvidos

Exemplo 1: Uma população de bactérias dobra a cada hora. Se no início havia 100 bactérias, quantas existirão após 5 horas?

Fórmula: $P(t) = P_0 \cdot 2^t$ $P(5) = 100 \cdot 2^5 = 100 \cdot 32 = 3200$. Resposta: Após 5 horas, existirão 3200 bactérias.

Exemplo 2: Um capital de R$ 5000 cresce 20% ao mês em juros compostos. Qual será o valor após 6 meses?

Fórmula: $M = P \cdot (1+i)^t$ $M = 5000 \cdot (1+0,20)^6 = 5000 \cdot (1,2)^6 \approx 14.921,92$. Resposta: Após 6 meses, o capital será de aproximadamente R$ 14.921,92.

📘 Aprimore seus estudos em funções e crescimento com nosso material exclusivo!
Baixe grátis o eBook Fórmulas Matemática

6) Exercícios propostos

Uma população de 50 coelhos dobra a cada mês. Quantos coelhos existirão após 8 meses?
Um investimento de R$ 2000 rende 10% ao mês. Qual será o valor acumulado após 12 meses?
Uma bactéria se divide a cada 20 minutos. Quantas células existirão após 2 horas, começando com 1 célula?

📚 Produtos recomendados

🧠 Mapas Mentais de Matemática 🎯 ENEM Matemática 📚 Coleção 10 eBooks 📝 Banco de Questões 📘 eBook Fórmulas Matemática

Relacionadas

Imagem função exponencial

Aplicações da Função Exponencial

Função Exponencial

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.