CUBO – Geometria Espacial
Fórmulas, Volume, Área Total e Diagonal Espacial
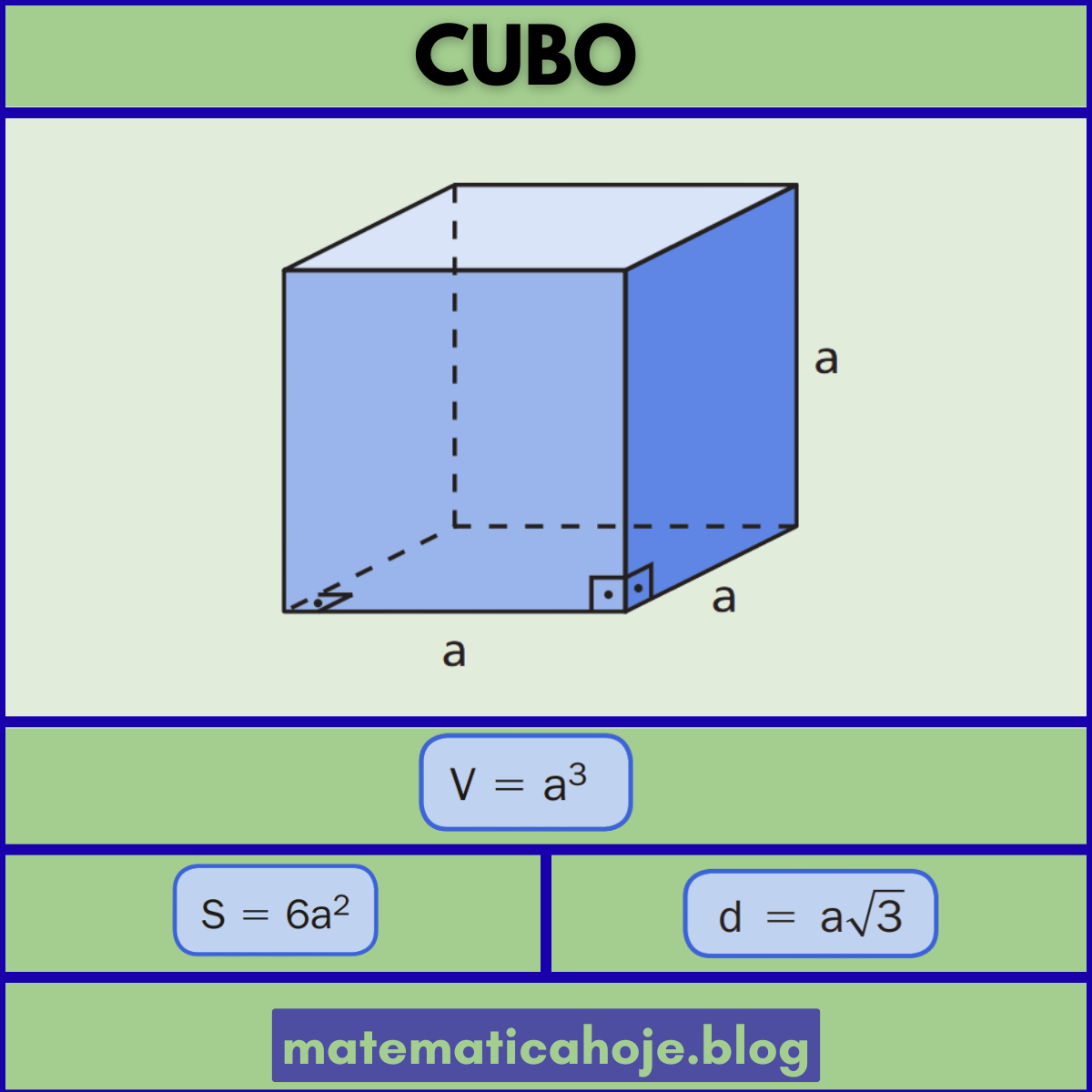
O que é um cubo?
O cubo é um sólido da Geometria Espacial com seis faces quadradas congruentes, 12 arestas iguais e 8 vértices. É um caso especial do paralelepípedo retângulo em que todas as dimensões são iguais.
🧠 Mapas Mentais de Matemática
📘 Banco de Questões
🎯 Guia do ENEM
📚 Coleção completa
📘 Fórmulas do Cubo
Seja a a medida da aresta do cubo:
Exemplo 1
Um cubo possui aresta \( a = 4\,\text{cm} \). Calcule seu volume, área total e diagonal espacial.
📗 Baixe o eBook de Fórmulas Matemáticas
Tenha todas as fórmulas de Geometria Espacial, Álgebra e Trigonometria em um único PDF.
📥 Baixar AgoraExemplos Adicionais
Exemplo 2: Um cubo tem volume de \( 125\,\text{cm}^3 \). Determine a aresta.
Exemplo 3: A diagonal espacial mede \( 10\sqrt{3}\,\text{cm} \). Calcule a área total.
Exercícios de Múltipla Escolha
1. Um cubo tem aresta de \( 3\,\text{cm} \). O volume é:
👀 Ver solução passo a passo
Gabarito: C.
2. A diagonal espacial de um cubo mede \( 6\sqrt{3}\,\text{cm} \). A aresta mede:
👀 Ver solução passo a passo
Gabarito: A.
3. A área total de um cubo é \( 150\,\text{cm}^2 \). O valor da aresta é:
👀 Ver solução passo a passo
Gabarito: C.
Conclusão
O estudo do cubo é essencial na Geometria Espacial e aparece com frequência em provas e no ENEM. Dominar as fórmulas facilita o entendimento de outros sólidos.




























