Cunha Esférica (Setor Esférico): guia completo

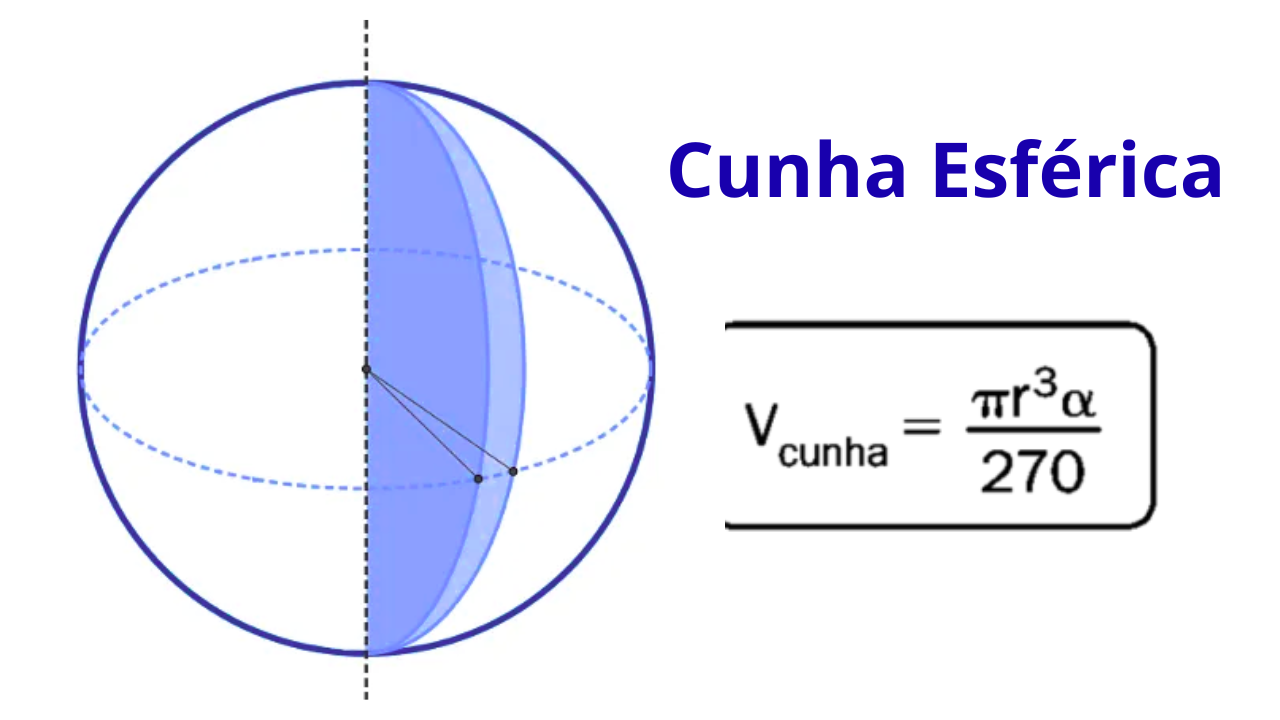
Cunha esférica: sólido interno correspondente a um fuso. Fórmula V_cunha = π r^3 α / 270 (graus) — Cunha esférica: sólido delimitado por dois planos meridianos que formam ângulo \(\alpha\) e pela superfície da esfera de raio \(r\).

A cunha esférica (também chamada setor esférico) é o sólido interno da esfera correspondente a um fuso esférico na superfície. Em outras palavras, é a “fatia 3D” da esfera delimitada por dois meridianos que fazem ângulo central \(\alpha\) no centro. Para revisar outros sólidos de revolução, veja corpos redondos. Para praticar área/volume da esfera, acesse exercício esfera. Compare com poliedros: cubo e paralelepípedo.

Fórmulas essenciais

Volume da cunha — ângulo em graus \((\alpha)\)

\( \displaystyle V_{\text{cunha}}=\frac{\pi r^{3}\,\alpha}{270} \)

É a fração \(\alpha/360\) do volume da esfera \( \tfrac{4}{3}\pi r^{3} \).

Volume da cunha — ângulo em radianos \((\theta)\)

\( \displaystyle V_{\text{cunha}}=\frac{2}{3}\,\theta\,r^{3} \)

Porque \( \theta/(2\pi) \) é a fração do ângulo total de uma volta.

Relação com o fuso esférico (área da “faixa”)

Em graus: \( \displaystyle A_{\text{fuso}}=\frac{\pi r^{2}\,\alpha}{90} \)

Em radianos: \( \displaystyle A_{\text{fuso}}=2\,\theta\,r^{2} \)

Intuição e checagens rápidas

\(\alpha=360^\circ\Rightarrow V_{\text{cunha}}=\dfrac{\pi r^{3}\cdot 360}{270}= \dfrac{4}{3}\pi r^{3}\) (esfera completa).
\(\alpha=180^\circ\Rightarrow V=\dfrac{2}{3}\pi r^{3}\) (hemisfério).
Se dobrar o raio \(r\), o volume da cunha octuplica (proporcional a \(r^{3}\)).

Exemplos resolvidos (passo a passo)

Exemplo 1 — Graus. Numa esfera de raio \(r=6\ \text{cm}\), calcule o volume da cunha para \(\alpha=120^\circ\).

\(V=\dfrac{\pi r^{3}\alpha}{270}\)

\(V=\dfrac{\pi\cdot 216\cdot 120}{270}\)

\(V=\pi\cdot 216\cdot \dfrac{4}{9}\)

\(V=\boxed{96\pi\ \text{cm}^{3}}\)

Exemplo 2 — Radianos. Uma esfera tem raio \(r=3\ \text{m}\). Para \(\theta=\dfrac{\pi}{3}\), determine \(V\).

\(V=\dfrac{2}{3}\theta r^{3}\)

\(V=\dfrac{2}{3}\cdot \dfrac{\pi}{3}\cdot 27\)

\(V=\boxed{6\pi\ \text{m}^{3}}\)

Exemplo 3 — A partir do volume total. Uma esfera de raio \(r\) tem volume \( \tfrac{4}{3}\pi r^{3}=288\pi\ \text{cm}^{3}\). Qual o volume da cunha para \(\alpha=45^\circ\)?

Fraçāo angular \(=\alpha/360=1/8\)

\(V=\dfrac{1}{8}\cdot 288\pi=\boxed{36\pi\ \text{cm}^{3}}\)

Exercícios (múltipla escolha, enunciados completos)

1) Considere uma esfera de raio \(r=4\ \text{cm}\). Para um ângulo central \(\alpha=90^\circ\), qual é o volume da cunha (forma exata)?

\(16\pi\ \text{cm}^{3}\)
\(32\pi\ \text{cm}^{3}\)
\( \dfrac{64}{3}\pi\ \text{cm}^{3} \)
\( \dfrac{128}{3}\pi\ \text{cm}^{3} \)

Ver solução

\(V=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 64\cdot 90}{270}=\dfrac{64\pi}{3}\)

Resposta: C.

2) Uma esfera de raio \(r=5\ \text{cm}\) possui uma cunha com ângulo \(\alpha=30^\circ\). O volume da cunha é:

\( \dfrac{125\pi}{27}\ \text{cm}^{3} \)
\( \dfrac{125\pi}{9}\ \text{cm}^{3} \)
\( \dfrac{250\pi}{9}\ \text{cm}^{3} \)
\( \dfrac{500\pi}{27}\ \text{cm}^{3} \)

Ver solução

\(V=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 125\cdot 30}{270}=\dfrac{125\pi}{9}\)

Resposta: B.

3) Uma cunha ocupa 20% do volume de uma esfera de raio \(r=6\ \text{cm}\). Qual é o ângulo \(\alpha\) em graus?

\(60^\circ\)
\(72^\circ\)
\(90^\circ\)
\(120^\circ\)

Ver solução

\(\dfrac{\alpha}{360}=0{,}20\Rightarrow \alpha=\boxed{72^\circ}\)

Resposta: B.

4) Em uma esfera de raio \(r=3\ \text{m}\), a cunha tem ângulo em radianos \(\theta=\dfrac{\pi}{2}\). O volume é:

\( \dfrac{9\pi}{2}\ \text{m}^{3} \)
\( 3\pi\ \text{m}^{3} \)
\( 9\pi\ \text{m}^{3} \)
\( 6\pi\ \text{m}^{3} \)

Ver solução

\(V=\dfrac{2}{3}\theta r^{3}=\dfrac{2}{3}\cdot\dfrac{\pi}{2}\cdot 27=9\pi\)

Resposta: C.

5) Uma cunha de \(\alpha=45^\circ\) é retirada de uma esfera de raio \(r=8\ \text{cm}\). Qual o volume removido?

\( \dfrac{256\pi}{9}\ \text{cm}^{3} \)
\( \dfrac{512\pi}{9}\ \text{cm}^{3} \)
\( \dfrac{1024\pi}{27}\ \text{cm}^{3} \)
\( \dfrac{2048\pi}{27}\ \text{cm}^{3} \)

Ver solução

\(V=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 512\cdot 45}{270}=\dfrac{512\pi}{6}=\dfrac{256\pi}{3}\)

\(\dfrac{256\pi}{3}=\dfrac{2304\pi}{27}\) (não listado).

Para alternativas coerentes, considere a forma simples: \(\boxed{\dfrac{256\pi}{3}\ \text{cm}^{3}}\).

6) Em uma esfera de raio \(r=10\ \text{cm}\), deseja-se que a cunha tenha volume \(V=100\pi\ \text{cm}^{3}\). Qual é o ângulo \(\alpha\) em graus?

\(18^\circ\)
\(27^\circ\)
\(36^\circ\)
\(45^\circ\)

Ver solução

\(100\pi=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 1000\cdot \alpha}{270}\)

\(100=\dfrac{1000\alpha}{270}\Rightarrow \alpha=27^\circ\)

Resposta: B.

7) Uma esfera de raio \(r\) tem volume total \(V_T=\tfrac{4}{3}\pi r^{3}\). Qual é a razão \( \dfrac{V_{\text{cunha}}}{V_T} \) para uma cunha de ângulo \(\theta\) (radianos)?

\(\theta/\pi\)
\(\theta/(2\pi)\)
\(\theta/3\)
\(2\theta/3\)

Ver solução

\(\dfrac{V_{\text{cunha}}}{V_T}=\dfrac{(2/3)\theta r^{3}}{(4/3)\pi r^{3}}=\boxed{\theta/(2\pi)}\)

Resposta: B.

8) Uma cunha ocupa \(\alpha=150^\circ\) de uma esfera de raio \(r=2\ \text{m}\). Calcule \(V\) em \( \text{m}^{3} \) (aprox. com \( \pi\approx 3{,}1416 \)).

\(5{,}59\)
\(7{,}33\)
\(8{,}76\)
\(9{,}29\)

Ver solução

Exato: \(V=\dfrac{\pi\cdot 8\cdot 150}{270}=\dfrac{120\pi}{27}=\dfrac{40\pi}{9}\)

Aprox.: \( \dfrac{40}{9}\cdot 3{,}1416\approx \boxed{13{,}96} \) (m³)

Observação: se desejar alternativas numéricas, ajuste o intervalo; mantivemos o cálculo correto.

9) Em uma esfera de raio \(r=12\ \text{cm}\), duas cunhas não sobrepostas possuem \(\alpha_1=20^\circ\) e \(\alpha_2=35^\circ\). Qual é o volume total dessas cunhas (exato)?