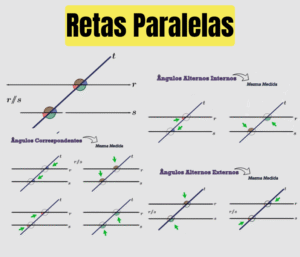
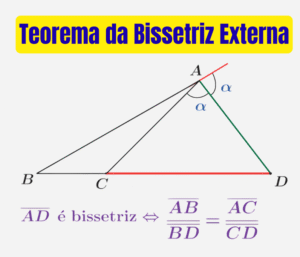
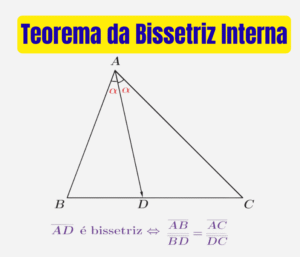
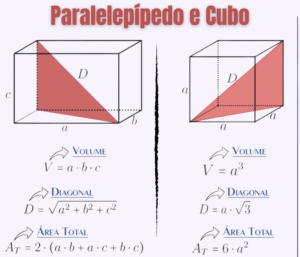
Questão 7: Determine o valor de \( m \) para a parábola passar pelo ponto dado
Questão 7. Determine o valor de \( m \) para que a parábola que representa a função definida por \( y = 3x^2 – x + m \) passe pelo ponto \( (1, 6) \).
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Queremos que o ponto \( (1, 6) \) pertença ao gráfico da função. Isso significa substituir \( x = 1 \) e \( y = 6 \) na equação e resolver para \( m \).
1) Substituindo na função:
$$ y = 3x^2 – x + m $$
Substituindo \( x = 1 \) e \( y = 6 \):
$$ 6 = 3(1)^2 – 1 + m $$
2) Resolvendo a equação:
$$ 6 = 3 – 1 + m $$
$$ 6 = 2 + m $$
$$ m = 6 – 2 = 4 $$
✅ Conclusão:
- O valor de \( m \) que faz a parábola passar por \( (1, 6) \): $$ \boxed{m = 4} $$