Distância entre Dois Pontos

Distância entre Dois Pontos — Fórmula, Explicação e Exercícios Resolvidos

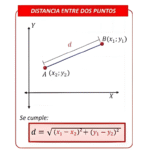
A distância entre dois pontos no plano cartesiano representa o comprimento do segmento de reta que os liga. Ela é uma das fórmulas mais importantes da Geometria Analítica e deriva diretamente do Teorema de Pitágoras.

Fórmula da distância entre dois pontos - matematicaoje.blog

📘 Fórmula Geral

Sejam dois pontos \( A(x_A, y_A) \) e \( B(x_B, y_B) \). A distância entre eles é dada por:

\( d = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2} \)

Essa fórmula expressa o valor do segmento de reta que une \(A\) e \(B\), calculado a partir das diferenças entre suas coordenadas.

🧮 Dedução da Fórmula

Ao projetar os pontos sobre os eixos, forma-se um triângulo retângulo cujos catetos são as diferenças entre as coordenadas:

Comprimento horizontal: \( |x_B – x_A| \)
Comprimento vertical: \( |y_B – y_A| \)

Aplicando o Teorema de Pitágoras:

\( d^2 = (x_B – x_A)^2 + (y_B – y_A)^2 \)

Tomando a raiz quadrada, obtemos a expressão final:

\( d = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2} \)

💡 Essa fórmula é útil para calcular distâncias entre cidades, posições no plano e até mesmo em problemas de Física que envolvem deslocamentos no espaço bidimensional.

📐 Exemplo 1 — Nível Fácil

Calcule a distância entre os pontos \( A(2, 3) \) e \( B(7, 3) \).

Como as ordenadas são iguais, a distância é apenas horizontal: \[ d = \sqrt{(7 – 2)^2 + (3 – 3)^2} = \sqrt{5^2} = 5 \] ✅ A distância entre os pontos é **5 unidades**.

📐 Exemplo 2 — Nível Médio

Determine a distância entre os pontos \( A(1, 2) \) e \( B(4, 6) \).

\[ d = \sqrt{(4 – 1)^2 + (6 – 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \] ✅ A distância entre os pontos é **5 unidades**.

📐 Exemplo 3 — Nível Avançado

Encontre a distância entre \( A(-2, -3) \) e \( B(3, 5) \).

\[ d = \sqrt{(3 – (-2))^2 + (5 – (-3))^2} = \sqrt{(5)^2 + (8)^2} = \sqrt{25 + 64} = \sqrt{89} \] ✅ A distância entre os pontos é **\(\sqrt{89}\)** ≈ **9,43 unidades**.

📘 Exemplo 4 — Nível Desafio

Calcule a distância entre \( A(-4, 7) \) e \( B(5, -2) \).

\[ d = \sqrt{(5 – (-4))^2 + (-2 – 7)^2} = \sqrt{(9)^2 + (-9)^2} = \sqrt{81 + 81} = \sqrt{162} \] \[ d = 9\sqrt{2} \approx 12{,}73 \] ✅ A distância entre os pontos é **9√2** ou **aproximadamente 12,73 unidades**.

📘 eBook Fórmulas Matemática — Guia Completo de Estudos

Domine todas as fórmulas essenciais de Geometria Analítica, Trigonometria e Álgebra com o eBook Fórmulas Matemática. Ideal para provas e concursos!

📥 Baixar Agora — Grátis

📚 Continue Estudando

Relacionadas

Área de um Triângulo no Plano Cartesiano

Distância entre Dois Pontos

Coordenadas do Baricentro

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.