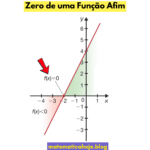
Domínio de uma função afim
O domínio de uma função é o conjunto de valores de \(x\) para os quais a função está definida. Para a função afim \(f(x)=ax+b\), o domínio natural é \( \mathbb{R} \), pois não há divisões por zero nem raízes de índice par restringindo \(x\).
![Dois gráficos da função 2x: à esquerda domínio ℝ; à direita domínio restrito [1,3] indicado no eixo x](https://matematicahoje.blog/wp-content/uploads/2025/09/Dominio-de-uma-funcao-Afim.png)
Quando o domínio NÃO é \( \mathbb{R} \)
- Restrição explícita no enunciado: “seja \(g(x)=2x\) definida em \([1,3]\)”. Então \(D(g)=[1,3]\).
- Contexto físico: tempo \(t\ge0\), quantidade \(q\in\mathbb{N}\), etc. Ex.: custo \(C(q)=20q+50\) com \(q\in\{0,1,2,\dots\}\) (domínio discreto).
- Definição por partes: “\(h(x)=-x+4\) se \(0\le x\le 2\)”. Logo \(D(h)=[0,2]\).
- Dados de tabela: o domínio é o conjunto dos \(x\) fornecidos na primeira coluna.
Como identificar o domínio em cada representação
- Pela lei: em \(ax+b\), assuma \(D=\mathbb{R}\), salvo restrição indicada.
- No gráfico: projete o traço da reta no eixo \(x\). O “sombra” formada (segmentos, intervalos) é o domínio.
- Na tabela: \(D\) é o conjunto de entradas (todos os \(x\) listados).
📘 Precisa revisar notação de conjuntos e intervalos?
Tenha à mão um resumo com símbolos, intervalos e propriedades das funções. Baixe o eBook Fórmulas Matemática.
Notações úteis para domínio
- \(D(f)=\mathbb{R}\) (todos os reais).
- \(D(f)=[a,b]\) (intervalo fechado), \((a,b)\) (aberto), \([a,b)\) ou \((a,b]\).
- \(D(f)=\{0,1,2,\dots\}\) (discreto).
- “Contra-domínio” (valores permitidos de saída) é diferente de imagem (valores efetivamente gerados). Aqui focamos no domínio.
Exemplos resolvidos
Exemplo 1 — Domínio natural. Determine \(D\) de \(f(x)=0{,}8x+3\) e interprete em um contexto de corrida por aplicativo.
Ver solução
Matematicamente, \(D(f)=\mathbb{R}\). No contexto, só faz sentido \(t\ge0\) (tempo) ⇒ \(D=\,[0,\infty)\).
Exemplo 2 — Domínio restrito por enunciado. Para \(g(x)=-2x+5\), “definida para \(x\in[-1,4]\)”. Encontre \(D(g)\) e a imagem.
Ver solução
\(D(g)=[-1,4]\). Como é afim e decrescente, a imagem é o intervalo entre \(g(-1)=7\) e \(g(4)=-3\): \([-3,7]\).
Exemplo 3 — Domínio discreto (tabela). Uma loja estima \(R(q)=12q+80\) com \(q\in\{0,1,2,3,4\}\). Qual é o domínio?
Ver solução
\(D=\{0,1,2,3,4\}\). (A lei é afim, mas o domínio é dado pelo conjunto de quantidades possíveis.)
Exemplo 4 — Por partes. Defina \(h(x)=\begin{cases}2x-1,& 1\le x\le 3\\ \text{indef.},& \text{caso contrário}\end{cases}\). Determine \(D(h)\).
Ver solução
\(D(h)=[1,3]\). Fora desse intervalo, a função não está definida.
Erros comuns
- Confundir domínio natural com o domínio do problema (contexto ou restrição dadas). Leia o enunciado!
- Incluir pontos fora do traço no gráfico: use a projeção no eixo \(x\) e respeite bolinhas abertas/fechadas.
- Domínio ≠ imagem: domínio fica no eixo \(x\); imagem, no eixo \(y\).
Exercícios propostos (com gabarito)
1) Diga o domínio natural de \(f(x)=3x-2\) e, em contexto, se \(x\) representa dias desde hoje.
Gabarito
Natural: \(\mathbb{R}\). No contexto: \(x\ge0\) ⇒ \([0,\infty)\).
2) “Seja \(g(x)=x+4\) definida em \((-2,5]\).” Escreva \(D(g)\) e represente em desigualdade.
Gabarito
\(D(g)=(-2,5]\) ⇔ \(-2<x\le5\).
3) A tabela traz \(x\in\{-1,0,2,7\}\) e \(f(x)=2x+1\). Qual é o domínio? É contínuo ou discreto?
Gabarito
\(D=\{-1,0,2,7\}\). Discreto.
4) No gráfico de uma reta, o traço aparece apenas de \(x=1\) a \(x=3\), com bolinhas fechadas nas extremidades. Qual é o domínio?
Gabarito
\([1,3]\).
5) Considere \(h(x)=-5x+9\) para “idades humanas \(x\) em anos”. Escreva o domínio plausível.
Gabarito
Por exemplo, \(x\in[0,120]\) (ajuste conforme o contexto dado).