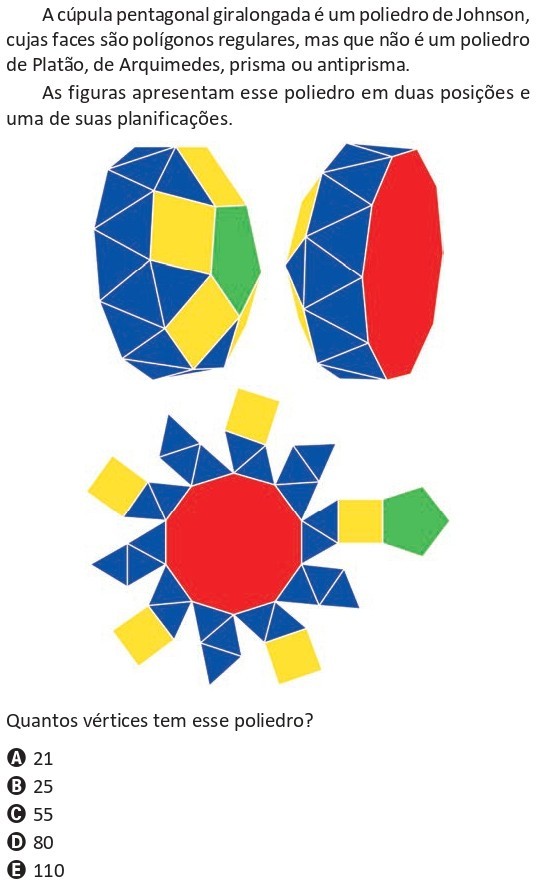
Nesta questão de Geometria Espacial do ENEM 2025, aparece um poliedro de Johnson chamado cúpula pentagonal giralongada. Suas faces são polígonos regulares (triângulos, quadrados, um pentágono e um decágono), mas ele não é um poliedro de Platão, de Arquimedes, prisma ou antiprisma. As figuras mostram o poliedro em duas vistas diferentes e também uma de suas planificações. A pergunta é: quantos vértices esse poliedro tem?
✅ Clique para ver a solução passo a passo
1) Contando as faces na planificação
Pela planificação, conseguimos ver claramente cada tipo de face do poliedro:
- Triângulos (azuis): 25 faces triangulares;
- Quadrados (amarelos): 5 faces quadradas;
- Pentágono (verde): 1 face pentagonal;
- Decágono (vermelho): 1 face decagonal.
Logo, o número total de faces é:
2) Determinando o número de arestas
Para achar o número de arestas, somamos o número de lados de todas as faces e depois dividimos por 2 (cada aresta é compartilhada por duas faces).
- Triângulos: 25 × 3 = 75 lados;
- Quadrados: 5 × 4 = 20 lados;
- Pentágono: 1 × 5 = 5 lados;
- Decágono: 1 × 10 = 10 lados.
Soma total de lados:
Como cada aresta aparece em duas faces:
3) Aplicando a relação de Euler
Para poliedros convexos, vale a relação de Euler:
Substituindo os valores encontrados:
Isolando V:
V = 2 + 23 = 25
Portanto, a cúpula pentagonal giralongada possui 25 vértices.
✅ Número de vértices do poliedro: 25
✅ Alternativa correta: B (25).
Antes desta questão de Geometria Espacial, resolvemos uma questão de Geometria Plana com escalas, analisando deslocamentos de um carrinho de brinquedo em diferentes escalas para descobrir qual era o maior deslocamento real. Você pode conferir essa resolução em: ENEM 2025 – Geometria Plana: escala e maior deslocamento .
Para reforçar seus estudos em Geometria Espacial, poliedros e demais conteúdos de Matemática para o ENEM, aproveite também:
🔎 Veja mais resoluções de Matemática do ENEM 2025 em:
https://matematicahoje.blog/category/matematica-enem-2025/













