Equação Geral da Reta

Equação Geral da Reta — Fórmula, Definição e Exercícios

A equação geral da reta é uma das formas mais utilizadas para representar retas no plano cartesiano. Essa forma é especialmente útil porque permite identificar facilmente o coeficiente angular e realizar comparações entre diferentes retas, como paralelismo e perpendicularidade.

Equação Geral da Reta - matematicaoje.blog

📘 Definição

Todas as equações das retas podem ser expressas na forma:

\( Ax + By + C = 0 \)

onde \( A \), \( B \) e \( C \) são números reais, e simultaneamente diferentes de zero.

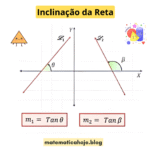
📐 Coeficiente Angular

O coeficiente angular \( m \) indica a inclinação da reta em relação ao eixo \( X \). Na equação geral, ele é calculado por:

\( m = -\dfrac{A}{B} \)

Observe que, se \( B = 0 \), a reta é vertical e não possui coeficiente angular definido.

💡 Dica: Se você transformar a equação geral na forma explícita \( y = mx + n \), o valor de \( m \) será o mesmo encontrado por \( -A/B \).

🧩 Exemplo Resolvido 1

Exemplo: Determine o coeficiente angular da reta dada pela equação \( 2x + 3y – 9 = 0 \).

Resolução:

\( m = -\dfrac{A}{B} = -\dfrac{2}{3} \)

Resposta: O coeficiente angular é \( m = -\dfrac{2}{3} \).

🧮 Exemplo Resolvido 2

Encontre o coeficiente angular da reta \( 5x – 4y + 8 = 0 \).

Resolução:

\( m = -\dfrac{A}{B} = -\dfrac{5}{-4} = \dfrac{5}{4} \)

Resposta: \( m = \dfrac{5}{4} \)

📘 Quer revisar todas as fórmulas de Geometria Analítica?
👉 Baixe grátis o eBook Fórmulas Matemática

📚 Exercícios de Fixação

1. Calcule o coeficiente angular da reta \( 3x + 2y – 6 = 0 \).

\( m = -\dfrac{A}{B} = -\dfrac{3}{2} \)

2. Determine o coeficiente angular da reta \( -4x + y + 5 = 0 \).

\( m = -\dfrac{-4}{1} = 4 \)

3 (Múltipla escolha). O coeficiente angular da reta \( 7x – 2y + 10 = 0 \) é:

A) \( \dfrac{2}{7} \)
B) \( -\dfrac{2}{7} \)
C) \( \dfrac{7}{2} \)
D) \( -\dfrac{7}{2} \)

\( m = -\dfrac{A}{B} = -\dfrac{7}{-2} = \dfrac{7}{2} \) ✅ Alternativa correta: C)

🔥 Exercícios Desafiadores

4. (Desafio 1) Encontre a equação geral da reta que tem coeficiente angular \( m = 2 \) e passa pelo ponto \( P(1, 3) \).

A equação genérica de uma reta é \( y – y_1 = m(x – x_1) \): \( y – 3 = 2(x – 1) \Rightarrow y – 3 = 2x – 2 \Rightarrow 2x – y + 1 = 0 \). Resposta: \( 2x – y + 1 = 0 \)

5. (Desafio 2) Determine a equação geral da reta que passa pelos pontos \( A(2, 3) \) e \( B(6, 5) \).

Primeiro, calcule o coeficiente angular: \( m = \dfrac{5 – 3}{6 – 2} = \dfrac{2}{4} = \dfrac{1}{2} \). Agora, usando \( y – y_1 = m(x – x_1) \): \( y – 3 = \dfrac{1}{2}(x – 2) \Rightarrow 2y – 6 = x – 2 \Rightarrow x – 2y + 4 = 0 \). Resposta: \( x – 2y + 4 = 0 \)

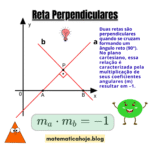
6. (Desafio 3) Verifique se as retas \( 2x – 3y + 6 = 0 \) e \( 4x – 6y – 10 = 0 \) são paralelas.

\( m_1 = -\dfrac{2}{-3} = \dfrac{2}{3} \)
\( m_2 = -\dfrac{4}{-6} = \dfrac{2}{3} \)
Como \( m_1 = m_2 \), ✔️ as retas são **paralelas**.

🔗 Continue Estudando

Relacionadas

Divisão de um Segmento em uma Razão Dada

Fórmula do Ponto Médio

Inclinação da Reta (Coeficiente Angular)

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.