Equação Simétrica da Reta

Equação Simétrica da Reta — Interseções com os Eixos X e Y

A equação simétrica da reta é uma forma especial de representar uma reta no plano cartesiano, destacando os pontos em que ela corta os eixos X e Y. Essa representação é especialmente útil para esboçar o gráfico de uma reta de forma rápida e intuitiva.

Equação Simétrica da Reta - matematicaoje.blog

📘 O que é a Equação Simétrica da Reta

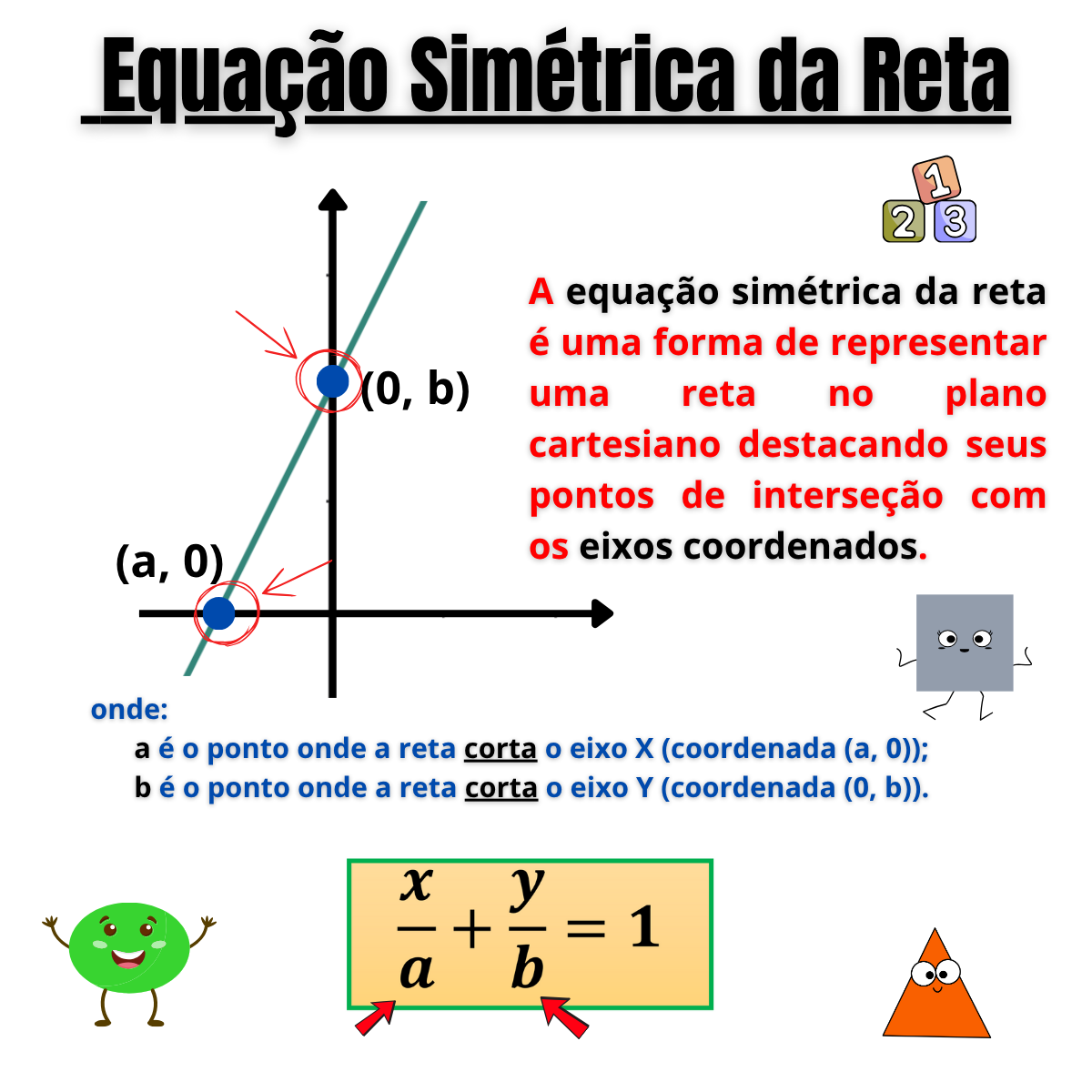
A equação simétrica de uma reta é expressa por:

\( \frac{x}{a} + \frac{y}{b} = 1 \)

Nessa forma de equação:

a é o ponto onde a reta corta o eixo X (coordenada \( (a, 0) \));
b é o ponto onde a reta corta o eixo Y (coordenada \( (0, b) \)).

Esses dois pontos são chamados de interceptos e indicam as interseções da reta com os eixos coordenados.

💡 Essa forma de equação é muito usada quando se deseja identificar rapidamente as interseções da reta com os eixos X e Y.

🧮 Interpretação Geométrica

O número a indica onde a reta encontra o eixo das abscissas (horizontal), e o número b indica onde a reta encontra o eixo das ordenadas (vertical). A equação relaciona de maneira proporcional as coordenadas \( x \) e \( y \) com esses pontos de corte, formando um triângulo com os eixos — o que facilita sua visualização geométrica.

📐 Exemplo 1

Exemplo: Considere a equação \( \frac{x}{4} + \frac{y}{2} = 1 \).

Essa reta corta o eixo X no ponto \( (4, 0) \) e o eixo Y no ponto \( (0, 2) \).

Com apenas esses dois pontos já é possível traçar o gráfico da reta.

📐 Exemplo 2

Exemplo: Dada a reta que passa pelos pontos \( (3, 0) \) e \( (0, 6) \), escreva sua equação simétrica.

Substituindo \( a = 3 \) e \( b = 6 \): \[ \frac{x}{3} + \frac{y}{6} = 1 \] Essa é a equação simétrica da reta.

📘 Consulte todas as fórmulas de Geometria Analítica no 👉 eBook Fórmulas Matemática

📚 Exercícios de Fixação

1. Determine os pontos de interseção da reta \( \frac{x}{2} + \frac{y}{3} = 1 \) com os eixos.

A reta corta o eixo X no ponto \( (2, 0) \) e o eixo Y no ponto \( (0, 3) \).

2. Escreva a equação simétrica da reta que intercepta o eixo X no ponto \( (5, 0) \) e o eixo Y no ponto \( (0, -2) \).

Substituindo \( a = 5 \) e \( b = -2 \): \[ \frac{x}{5} + \frac{y}{-2} = 1 \quad \Rightarrow \quad \frac{x}{5} – \frac{y}{2} = 1 \]

3. (Desafio) Encontre a equação simétrica da reta que corta o eixo X no ponto \( (6, 0) \) e o eixo Y no ponto \( (0, 4) \).

Substituindo \( a = 6 \) e \( b = 4 \): \[ \frac{x}{6} + \frac{y}{4} = 1 \]

🔗 Continue Estudando

Relacionadas

Coeficiente Angular da Reta

Fórmula do Ponto Médio

Divisão de um Segmento em uma Razão Dada

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.