Esfera: Área, Volume, Fuso Esférico e Cunha Esférica

A esfera é um dos principais corpos redondos. Todos os pontos da sua superfície estão à mesma distância do centro; essa distância é o raio \(r\). Para revisar a teoria geral, consulte Esfera e, para praticar, acesse Exercício Esfera. Compare com sólidos de faces planas: Cubo e Paralelepípedo.

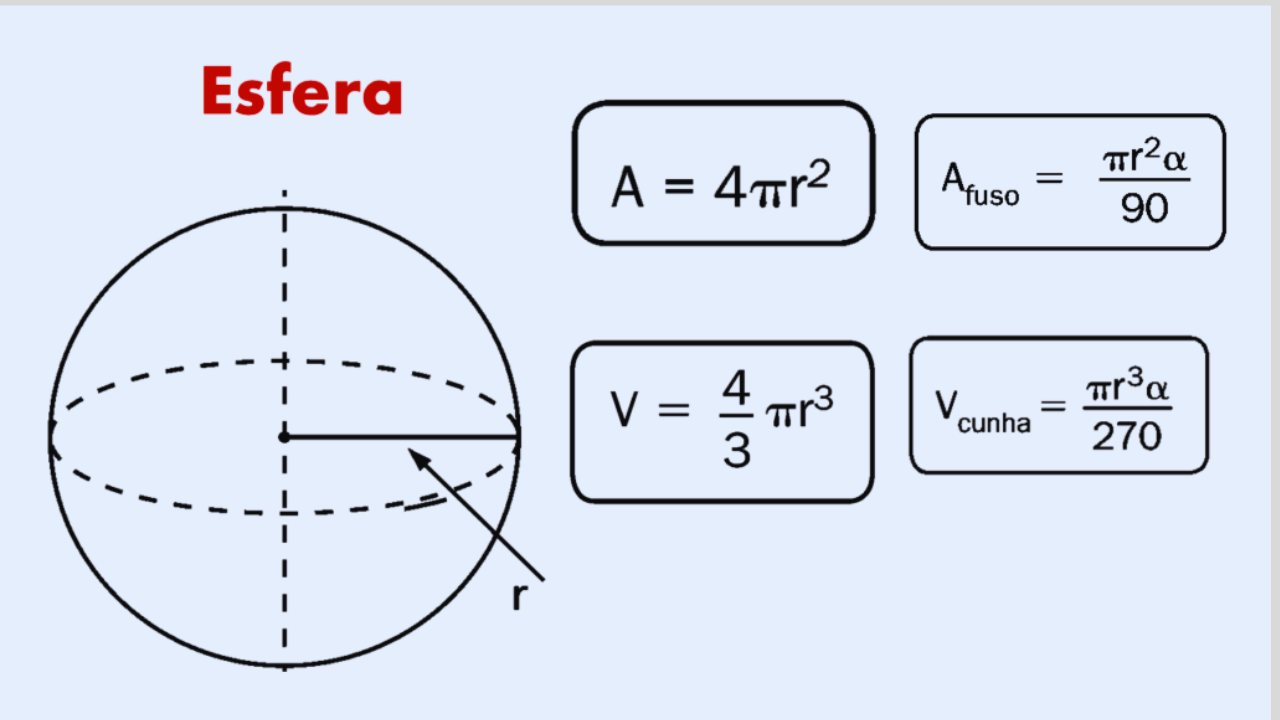
Esfera: A=4πr², V=4/3πr³, fuso e cunha esférica — Fórmulas fundamentais da esfera e de suas “fatias” angulares.

Fórmulas essenciais

Área da superfície da esfera

\( \displaystyle A = 4\pi r^{2} \)

Unidades quadradas (cm², m²…)
Com diâmetro \(d=2r\): \(A=\pi d^{2}\)

Volume da esfera

\( \displaystyle V = \frac{4}{3}\pi r^{3} \)

Unidades cúbicas (cm³, m³…)
Com diâmetro \(d\): \( \displaystyle V=\frac{\pi}{6}d^{3} \)

Fuso esférico e cunha esférica

Um fuso esférico (também chamado lúnula) é a “faixa” da superfície compreendida entre dois meridianos que formam ângulo central \(\alpha\). A cunha esférica (ou setor esférico) é o sólido correspondente no interior da esfera.

Área do fuso

Versão em graus: \( \displaystyle A_{\text{fuso}}=\frac{\pi r^{2}\alpha}{90} \)

Versão em radianos: \( \displaystyle A_{\text{fuso}}=2\theta\,r^{2} \)

onde \(\alpha\in[0,360]\)° e \(\theta=\alpha\cdot\pi/180\).

Volume da cunha

Versão em graus: \( \displaystyle V_{\text{cunha}}=\frac{\pi r^{3}\alpha}{270} \)

Versão em radianos: \( \displaystyle V_{\text{cunha}}=\frac{2}{3}\theta\,r^{3} \)

Proporcionalidade: tanto o fuso quanto a cunha são frações da área/volume total da esfera, diretamente proporcionais ao ângulo (\(\alpha\) em graus ou \(\theta\) em radianos). Exemplos: \(\alpha=180^\circ\) → hemisfério \((A=2\pi r^{2},\ V= \tfrac{2}{3}\pi r^{3})\); \(\alpha=360^\circ\) → esfera inteira.

Intuição/derivação curta

De \(V\) para \(A\): \( \displaystyle \frac{d}{dr}\!\left(\frac{4}{3}\pi r^{3}\right)=4\pi r^{2}=A \). A área é a taxa de variação do volume quando o raio cresce.
Regra de três angular: a área da esfera é \(4\pi r^{2}\) para \(360^\circ\). Logo, para \(\alpha^\circ\), \(A_{\text{fuso}}=\dfrac{\alpha}{360}\cdot 4\pi r^{2}=\dfrac{\pi r^{2}\alpha}{90}\). Idem para o volume: \(V_{\text{cunha}}=\dfrac{\alpha}{360}\cdot \dfrac{4}{3}\pi r^{3}=\dfrac{\pi r^{3}\alpha}{270}\).

Erros comuns

Confundir unidades: \(A\) em m²/cm² e \(V\) em m³/cm³.
Usar \(r^{3}\) na área (é \(r^{2}\)).
Esquecer de converter graus ↔ radianos ao aplicar as fórmulas com \(\theta\).

Exemplos resolvidos

Exemplo 1 — Área e volume da esfera. Para \(r=6\ \text{cm}\), calcule \(A\) e \(V\).

\(A=4\pi r^{2}\)

\(A=4\pi\cdot 6^{2}\)

\(A=4\pi\cdot 36=144\pi\ \text{cm}^{2}\)

\(V=\dfrac{4}{3}\pi r^{3}\)

\(V=\dfrac{4}{3}\pi\cdot 6^{3}\)

\(V=\dfrac{4}{3}\pi\cdot 216=288\pi\ \text{cm}^{3}\)

Exemplo 2 — Fuso e cunha (graus). Para \(r=5\ \text{cm}\) e \(\alpha=120^\circ\), encontre \(A_{\text{fuso}}\) e \(V_{\text{cunha}}\) (exatos).

\(A_{\text{fuso}}=\dfrac{\pi r^{2}\alpha}{90}=\dfrac{\pi\cdot 25\cdot 120}{90}\)

\(A_{\text{fuso}}=\dfrac{25\pi\cdot 120}{90}=\dfrac{25\pi\cdot 4}{3}=\boxed{\dfrac{100}{3}\pi\ \text{cm}^{2}}\)

\(V_{\text{cunha}}=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 125\cdot 120}{270}\)

\(V_{\text{cunha}}=\dfrac{125\pi\cdot 120}{270}=\dfrac{125\pi\cdot 4}{9}=\boxed{\dfrac{500}{9}\pi\ \text{cm}^{3}}\)

Exemplo 3 — Fuso e cunha (radianos). Para \(r=3\ \text{m}\) e \(\theta=\dfrac{\pi}{3}\), calcule \(A_{\text{fuso}}\) e \(V_{\text{cunha}}\).

\(A_{\text{fuso}}=2\theta r^{2}=2\cdot \dfrac{\pi}{3}\cdot 9=\boxed{6\pi\ \text{m}^{2}}\)

\(V_{\text{cunha}}=\dfrac{2}{3}\theta r^{3}=\dfrac{2}{3}\cdot \dfrac{\pi}{3}\cdot 27=\boxed{6\pi\ \text{m}^{3}}\)

Exercícios (múltipla escolha)

Em todos, use \(A=4\pi r^{2}\), \(V=\tfrac{4}{3}\pi r^{3}\), \(A_{\text{fuso}}=\dfrac{\pi r^{2}\alpha}{90}\) e \(V_{\text{cunha}}=\dfrac{\pi r^{3}\alpha}{270}\) (para \(\alpha\) em graus). Em radianos (\(\theta\)): \(A_{\text{fuso}}=2\theta r^{2}\) e \(V_{\text{cunha}}=\dfrac{2}{3}\theta r^{3}\).

1) Uma esfera tem raio \(4\ \text{cm}\). O par \((A,V)\) correto é:

\((64\pi\ \text{cm}^{2},\ 64\pi\ \text{cm}^{3})\)
\((64\pi\ \text{cm}^{2},\ \tfrac{256}{3}\pi\ \text{cm}^{3})\)
\((32\pi\ \text{cm}^{2},\ \tfrac{256}{3}\pi\ \text{cm}^{3})\)
\((32\pi\ \text{cm}^{2},\ 64\pi\ \text{cm}^{3})\)

Ver solução

\(A=4\pi r^{2}=4\pi\cdot 4^{2}=64\pi\ \text{cm}^{2}\)

\(V=\dfrac{4}{3}\pi r^{3}=\dfrac{4}{3}\pi\cdot 4^{3}=\dfrac{256}{3}\pi\ \text{cm}^{3}\)

Resposta: B.

2) Para uma esfera com área total \(A=144\pi\ \text{cm}^{2}\), calcule a área de um fuso de \(\alpha=45^\circ\) e o volume da cunha correspondente.

\(18\pi\ \text{cm}^{2}\) e \(36\pi\ \text{cm}^{3}\)
\(36\pi\ \text{cm}^{2}\) e \(18\pi\ \text{cm}^{3}\)
\(12\pi\ \text{cm}^{2}\) e \(24\pi\ \text{cm}^{3}\)
\(24\pi\ \text{cm}^{2}\) e \(12\pi\ \text{cm}^{3}\)

Ver solução

\(4\pi r^{2}=144\pi\Rightarrow r^{2}=36\Rightarrow r=6\ \text{cm}\)

\(A_{\text{fuso}}=\dfrac{\pi r^{2}\alpha}{90}=\dfrac{\pi\cdot 36\cdot 45}{90}=18\pi\ \text{cm}^{2}\)

\(V_{\text{cunha}}=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 216\cdot 45}{270}=36\pi\ \text{cm}^{3}\)

Resposta: A.

3) Para \(r=7\ \text{cm}\) e \(\alpha=180^\circ\) (hemisfério), a área curva e o volume são, respectivamente:

\(98\pi\ \text{cm}^{2}\) e \(\tfrac{686}{3}\pi\ \text{cm}^{3}\)
\(196\pi\ \text{cm}^{2}\) e \(\tfrac{343}{3}\pi\ \text{cm}^{3}\)
\(49\pi\ \text{cm}^{2}\) e \(\tfrac{343}{6}\pi\ \text{cm}^{3}\)
\(98\pi\ \text{cm}^{2}\) e \(343\pi\ \text{cm}^{3}\)

Ver solução

Área curva (meia esfera): \(2\pi r^{2}=2\pi\cdot 49=98\pi\ \text{cm}^{2}\)

Volume (metade): \(\dfrac{1}{2}\cdot \dfrac{4}{3}\pi r^{3}=\dfrac{2}{3}\pi\cdot 343=\dfrac{686}{3}\pi\ \text{cm}^{3}\)

Resposta: A.

4) Em radianos: para \(r=10\ \text{cm}\) e \(\theta=\dfrac{\pi}{6}\), determine \(A_{\text{fuso}}\) e \(V_{\text{cunha}}\).

\(\dfrac{100\pi}{3}\ \text{cm}^{2}\) e \(\dfrac{1000\pi}{9}\ \text{cm}^{3}\)
\(\dfrac{50\pi}{3}\ \text{cm}^{2}\) e \(\dfrac{500\pi}{9}\ \text{cm}^{3}\)
\(100\pi\ \text{cm}^{2}\) e \(1000\pi\ \text{cm}^{3}\)
\(\dfrac{200\pi}{3}\ \text{cm}^{2}\) e \(\dfrac{2000\pi}{9}\ \text{cm}^{3}\)

Ver solução

\(A_{\text{fuso}}=2\theta r^{2}=2\cdot \dfrac{\pi}{6}\cdot 100=\dfrac{100\pi}{3}\ \text{cm}^{2}\)

\(V_{\text{cunha}}=\dfrac{2}{3}\theta r^{3}=\dfrac{2}{3}\cdot \dfrac{\pi}{6}\cdot 1000=\dfrac{1000\pi}{9}\ \text{cm}^{3}\)

Resposta: A.

5) Uma esfera tem \(V=36\pi\ \text{cm}^{3}\). Para que a cunha tenha volume \(12\pi\ \text{cm}^{3}\), o ângulo \(\alpha\) (em graus) deve ser:

\(60^\circ\)
\(90^\circ\)
\(120^\circ\)
\(180^\circ\)

Ver solução

\(\dfrac{4}{3}\pi r^{3}=36\pi\Rightarrow r=3\ \text{cm}\)

\(V_{\text{cunha}}=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 27\cdot \alpha}{270}=\dfrac{\pi\alpha}{10}\)

\(\dfrac{\pi\alpha}{10}=12\pi\Rightarrow \alpha=\boxed{120^\circ}\)

Resposta: C.

6) Uma cúpula esférica de raio \(8\ \text{m}\) será pintada apenas em um fuso de \(\alpha=60^\circ\). A área a pintar é, aproximadamente:

\(101\ \text{m}^{2}\)
\(120{,}6\ \text{m}^{2}\)
\(134{,}0\ \text{m}^{2}\)
\(201{,}1\ \text{m}^{2}\)

Ver solução

\(A_{\text{fuso}}=\dfrac{\pi r^{2}\alpha}{90}=\dfrac{\pi\cdot 64\cdot 60}{90}=\dfrac{128}{3}\pi\approx \boxed{134{,}0\ \text{m}^{2}}\)

Resposta: C.

7) Quantas cunhas esféricas de \(\alpha=30^\circ\) são necessárias para compor a esfera inteira?

Ver solução

Cada cunha corresponde a \(\alpha/360=30/360=1/12\) da esfera.

\(\Rightarrow\) Número de cunhas \(=360/30=\boxed{12}\).

Resposta: C.

8) Sabe-se que um fuso de \(\alpha=90^\circ\) tem área \(200\pi\ \text{cm}^{2}\). Determine o raio e o volume da cunha correspondente (exatos).

\(r=10\ \text{cm}\) e \(V=\dfrac{1000}{3}\pi\ \text{cm}^{3}\)
\(r=10\sqrt{2}\ \text{cm}\) e \(V=\dfrac{2000\sqrt{2}}{3}\pi\ \text{cm}^{3}\)
\(r=20\ \text{cm}\) e \(V=\dfrac{8000}{3}\pi\ \text{cm}^{3}\)
\(r=5\sqrt{2}\ \text{cm}\) e \(V=\dfrac{250\sqrt{2}}{3}\pi\ \text{cm}^{3}\)

Ver solução

Para \(\alpha=90^\circ\): \(A_{\text{fuso}}=\dfrac{\pi r^{2}\cdot 90}{90}=\pi r^{2}\)

\(\pi r^{2}=200\pi\Rightarrow r^{2}=200\Rightarrow r=\boxed{10\sqrt{2}\ \text{cm}}\)

\(V_{\text{cunha}}=\dfrac{\pi r^{3}\cdot 90}{270}=\dfrac{\pi r^{3}}{3}=\dfrac{\pi(10\sqrt{2})^{3}}{3}=\boxed{\dfrac{2000\sqrt{2}}{3}\pi\ \text{cm}^{3}}\)

Resposta: B.