Exercício Cilindro – coleção com 15 situações-problema de múltipla escolha, em ordem crescente de dificuldade. Para revisar teoria, veja Corpos redondos, o resumo de Cone e a página da Esfera. Se precisar das fórmulas do cilindro (área lateral, total e volume), consulte também o artigo principal sobre o tema.
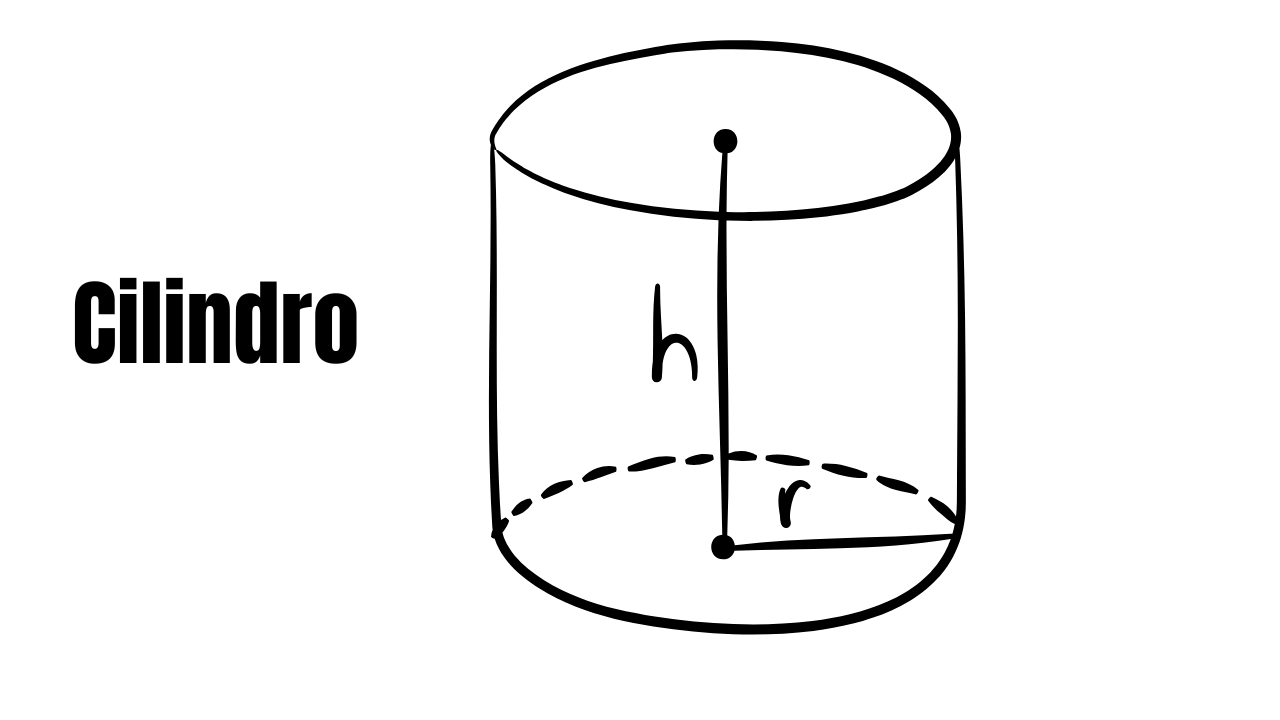
Notação usada nos enunciados: \(r\) = raio da base (raio do círculo da base); \(h\) = altura do cilindro (distância perpendicular entre os planos das bases); \(g\) = geratriz do cilindro oblíquo (comprimento da lateral inclinada). Use \(\pi\approx3{,}1416\) nas contas com aproximação.
1) Uma lata cilíndrica tem raio da base \(r=4\,\text{cm}\) e altura \(h=10\,\text{cm}\). Qual é a capacidade em litros?
- 0,45 L
- 0,50 L
- 0,55 L
- 0,60 L
Mostrar solução
\(V=\pi r^2h=160\pi\approx 502{,}65\,\text{cm}^3=0{,}503\,\text{L}\) → alternativa B.
2) Um cilindro reto tem raio \(r=3\,\text{cm}\) e altura \(h=12\,\text{cm}\). Qual a área do rótulo (apenas a superfície lateral)?
- 188,5 cm²
- 226,2 cm²
- 251,3 cm²
- 282,7 cm²
Mostrar solução
\(A_L=2\pi rh=72\pi\approx \mathbf{226{,}19}\ \text{cm}^2\) → B.
3) Um vaso cilíndrico fechado (duas tampas) possui raio \(r=5\,\text{cm}\) e altura \(h=8\,\text{cm}\). Qual é a área total externa a ser pintada?
- 377,0 cm²
- 392,7 cm²
- 408,4 cm²
- 424,1 cm²
Mostrar solução
\(A_T=2\pi r(h+r)=2\pi\cdot5(8+5)=130\pi\approx \mathbf{408{,}41}\ \text{cm}^2\) → C.
4) Uma lata cilíndrica fechada será pintada por fora. Dados: raio \(r=6\,\text{cm}\), altura \(h=15\,\text{cm}\) e preço de R$ 0,02 por cm². Qual o custo?
- R$ 12,60
- R$ 14,90
- R$ 15,83
- R$ 17,20
Mostrar solução
\(A_T=2\pi r(h+r)=252\pi\approx 791{,}68\ \text{cm}^2\). Custo \(=0{,}02\cdot791{,}68\approx \mathbf{R\$\,15{,}83}\) → C.
5) Um tanque cilíndrico tem raio \(r=1\,\text{m}\) e altura \(h=3\,\text{m}\), mas está preenchido apenas até metade da altura. Qual é o volume de água em litros?
- 3 770 L
- 4 712 L
- 5 240 L
- 6 283 L
Mostrar solução
Metade da altura \(\Rightarrow\) metade do volume: \(V=\pi r^2(h/2)=1{,}5\pi\ \text{m}^3\approx \mathbf{4\,712}\ \text{L}\) → B.
6) Um cilindro oblíquo tem raio \(r=4\,\text{cm}\) e geratriz \(g=13\,\text{cm}\) (comprimento da lateral inclinada). Qual é a área lateral?
- 288π cm²
- 104π cm²
- 120π cm²
- 130π cm²
Mostrar solução
No oblíquo \(A_L=2\pi rg=2\pi\cdot4\cdot13=\mathbf{104\pi}\approx 326{,}73\ \text{cm}^2\) → B.
7) Uma chapa retangular \(25\times20\,\text{cm}\) forma o rótulo de uma lata ao ser enrolada, usando 25 cm como circunferência da base. Assim, o raio é \(r=\frac{25}{2\pi}\) e a altura é \(h=20\,\text{cm}\). Qual é o volume da lata?
- 905 cm³
- 995 cm³
- 1 050 cm³
- 1 120 cm³
Mostrar solução
\(r=\frac{25}{2\pi}\approx 3{,}979\). \(V=\pi r^2h\approx \mathbf{994{,}72}\ \text{cm}^3\) → alternativa B.
8) Para minimizar a área total com volume fixo, uma lata deve satisfazer \(h=2r\). Se o volume desejado é \(1\,000\,\text{cm}^3\), quais dimensões mais próximas atendem essa condição?
- \(r=4{,}8\) cm; \(h=9{,}6\) cm
- \(r=5{,}4\) cm; \(h=10{,}8\) cm
- \(r=6{,}0\) cm; \(h=12{,}0\) cm
- \(r=7{,}0\) cm; \(h=14{,}0\) cm
Mostrar solução
\(r=(V/2\pi)^{1/3}\approx 5{,}42\) e \(h\approx 10{,}84\). Alternativa mais próxima: B.
9) Um tubo cilíndrico tem raio externo \(R=8\,\text{cm}\), raio interno \(r=5\,\text{cm}\) e comprimento (altura) \(h=30\,\text{cm}\). Qual o volume de metal (diferença entre os volumes)?
- 2 827 cm³
- 3 142 cm³
- 3 676 cm³
- 4 189 cm³
Mostrar solução
\(V=\pi(R^2-r^2)h=\pi(64-25)\cdot30=1170\pi\approx \mathbf{3\,675{,}66}\ \text{cm}^3\) → C.
10) Moedas cilíndricas de diâmetro \(2{,}4\,\text{cm}\) (logo \(r=1{,}2\,\text{cm}\)) e espessura \(0{,}2\,\text{cm}\) são empilhadas em 10 unidades (\(h=2\,\text{cm}\)). Qual é o volume do rolo?
- 7,85 cm³
- 9,05 cm³
- 10,20 cm³
- 12,57 cm³
Mostrar solução
\(V=\pi r^2h=\pi\cdot1{,}2^2\cdot2=2{,}88\pi\approx \mathbf{9{,}05}\ \text{cm}^3\) → B.
11) Um reservatório cilíndrico de raio \(r=15\,\text{cm}\) e altura \(h=40\,\text{cm}\) está 2/3 cheio. Quantos litros faltam para completar?
- 7,85 L
- 9,42 L
- 10,47 L
- 12,57 L
Mostrar solução
Falta \(1/3\) do total: \(V_T=\pi r^2h=9000\pi\ \text{cm}^3\). \(V_{\text{faltante}}=3000\pi\approx \mathbf{9{,}425}\ \text{L}\) → B.
12) Uma fábrica mantém o raio \(r\) da lata e reduz a altura \(h\) em 10%. Em que percentual a área do rótulo \(A_L=2\pi rh\) diminui?
- 5%
- 10%
- 15%
- 20%
Mostrar solução
\(A_L\) é diretamente proporcional a \(h\); reduzindo \(h\) em \(10\%\), \(A_L\) também reduz \(10\%\) → B.
13) Um cone e um cilindro têm mesma base (mesmo raio \(r\)) e mesma altura \(h\). Se o volume do cone é \(1\,500\,\text{cm}^3\), qual é o volume do cilindro?
- 2 000 cm³
- 3 000 cm³
- 4 500 cm³
- 6 000 cm³
Mostrar solução
\(V_{\text{cil}}=3\,V_{\text{cone}}=3\cdot1\,500=\mathbf{4\,500}\ \text{cm}^3\) → C. (Veja cone.)
14) Em um protótipo cilíndrico, todas as dimensões foram ampliadas em 50% (isto é, \(r\) e \(h\) multiplicados por \(1{,}5\)). De quanto o volume aumentou?
- 150%
- 200%
- 237,5%
- 300%
Mostrar solução
Fator volumétrico \(=1{,}5^3=3{,}375\). Aumento relativo \(=3{,}375-1=\mathbf{2{,}375}=237{,}5\%\) → C.
15) Deseja-se um cilindro sem tampas (só lateral) com área lateral fixa \(S=600\pi\,\text{cm}^2\). Adote o projeto \(h=2r\). Quais dimensões e volume resultante?
- \(r\approx 10{,}0\) cm; \(h\approx 20{,}0\) cm; \(V\approx 9{,}425\ \text{cm}^3\)
- \(r\approx 11{,}0\) cm; \(h\approx 22{,}0\) cm; \(V\approx 10{,}600\ \text{cm}^3\)
- \(r\approx 12{,}25\) cm; \(h\approx 24{,}49\) cm; \(V\approx 11{,}543\ \text{cm}^3\)
- \(r\approx 13{,}0\) cm; \(h\approx 26{,}0\) cm; \(V\approx 12{,}400\ \text{cm}^3\)
Mostrar solução
Com \(S=2\pi rh\) e \(h=2r\): \(S=4\pi r^2\Rightarrow r=\sqrt{S/(4\pi)}=\sqrt{150}\approx \mathbf{12{,}247}\,\text{cm}\); \(h=2r\approx \mathbf{24{,}495}\,\text{cm}\).
\(V=\pi r^2h=\pi\cdot150\cdot24{,}495\approx \mathbf{11\,542{,}95}\ \text{cm}^3\) → alternativa C.
Quer seguir praticando? Explore os resumos de Corpos redondos, a página da Esfera e a seção de Cone. Se preferir, posso transformar esta lista em PDF/Word para impressão.






















