Exercício Fuso Esférico — 15 questões com soluções

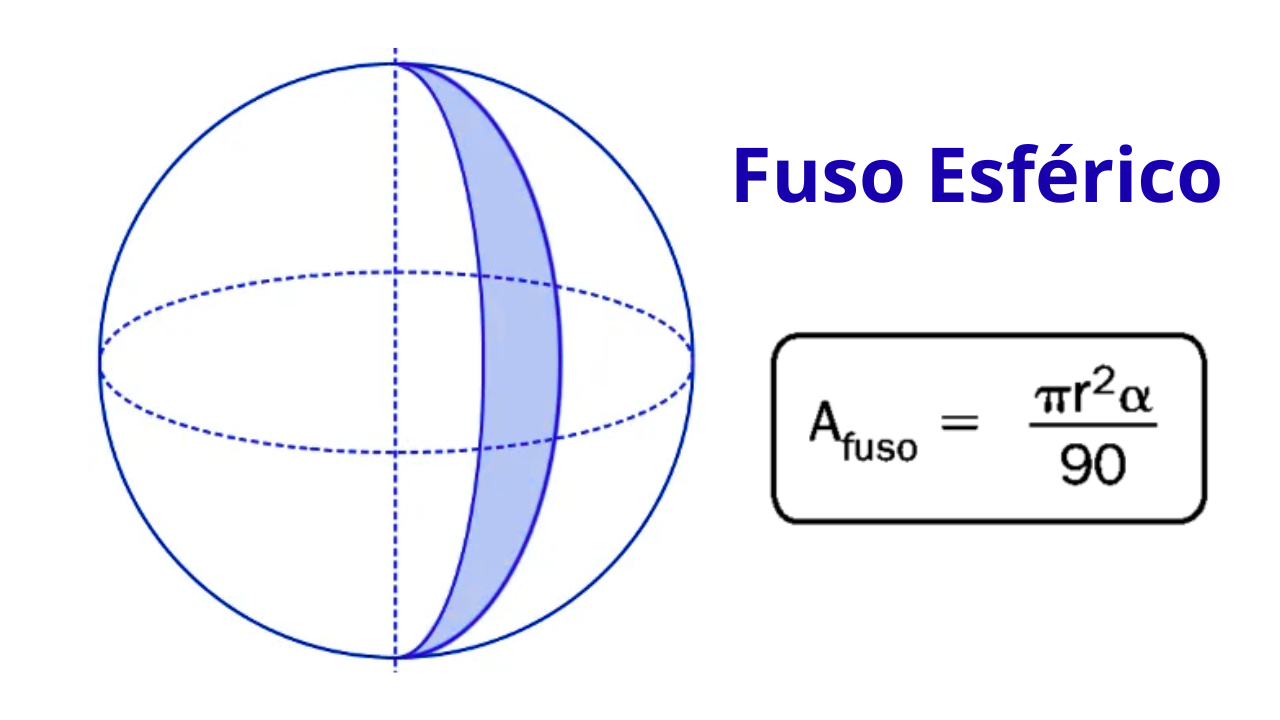
Fuso esférico (lúnula) delimitado por dois meridianos com ângulo central α — Fuso esférico (lúnula) entre dois meridianos que formam o ângulo central $\alpha$.

Antes de começar, revise a teoria em Esfera, o panorama em Corpos redondos e, para treinar volume/área da esfera, veja Exercício Esfera. Para contraste com poliedros, consulte Cubo e Paralelepípedo. Quando o enunciado pedir aproximações, use $ \pi \approx 3{,}1416 $.

Fórmulas essenciais

Em graus $(\alpha)$: $ \displaystyle A_{\text{fuso}}=\frac{\pi r^{2}\alpha}{90} \quad$ e $\quad \displaystyle V_{\text{cunha}}=\frac{\pi r^{3}\alpha}{270} $.

Em radianos $(\theta)$: $ \displaystyle A_{\text{fuso}}=2\,\theta\,r^{2} \quad$ e $\quad \displaystyle V_{\text{cunha}}=\frac{2}{3}\,\theta\,r^{3} $.

1) Direto e curto. Numa esfera de raio $r=3\ \text{cm}$, a área do fuso de $\alpha=60^\circ$ é:

$3\pi\ \text{cm}^{2}$
$6\pi\ \text{cm}^{2}$
$9\pi\ \text{cm}^{2}$
$12\pi\ \text{cm}^{2}$

Ver solução

$A_f=\dfrac{\pi r^{2}\alpha}{90}$

$A_f=\dfrac{\pi\cdot 9\cdot 60}{90}$

$A_f=\dfrac{9\pi\cdot 2}{3}= \boxed{6\pi\ \text{cm}^{2}}$

Resposta: B.

2) Com fração de círculo. Para $r=5\ \text{cm}$ e $\alpha=45^\circ$, a área do fuso é:

$10\pi\ \text{cm}^{2}$
$\dfrac{25\pi}{2}\ \text{cm}^{2}$
$15\pi\ \text{cm}^{2}$
$20\pi\ \text{cm}^{2}$

Ver solução

$A_f=\dfrac{\pi\cdot 25\cdot 45}{90}=\dfrac{25\pi}{2}\ \text{cm}^{2}$

Resposta: B.

3) Descobrindo o ângulo. Numa esfera de $r=4\ \text{cm}$, o fuso tem área $A_f=8\pi\ \text{cm}^{2}$. O ângulo central é:

$30^\circ$
$45^\circ$
$60^\circ$
$90^\circ$

Ver solução

$8\pi=\dfrac{\pi\cdot 16\cdot \alpha}{90}$

$8=\dfrac{16\alpha}{90}\Rightarrow \alpha=\dfrac{8\cdot 90}{16}=\boxed{45^\circ}$

Resposta: B.

4) Versão em radianos. Para $r=10\ \text{cm}$ e $\theta=\dfrac{\pi}{6}$, a área do fuso vale:

$\dfrac{50\pi}{3}\ \text{cm}^{2}$
$\dfrac{100\pi}{3}\ \text{cm}^{2}$
$\dfrac{200\pi}{3}\ \text{cm}^{2}$
$100\pi\ \text{cm}^{2}$

Ver solução

$A_f=2\theta r^{2}=2\cdot\dfrac{\pi}{6}\cdot 100=\boxed{\dfrac{100\pi}{3}\ \text{cm}^{2}}$

Resposta: B.

5) Hemisfério (checagem). Com $r=7\ \text{cm}$ e $\alpha=180^\circ$, a área do fuso é:

$49\pi\ \text{cm}^{2}$
$98\pi\ \text{cm}^{2}$
$147\pi\ \text{cm}^{2}$
$196\pi\ \text{cm}^{2}$

Ver solução

Meia esfera (área curva): $2\pi r^{2}=2\pi\cdot 49=\boxed{98\pi}\ \text{cm}^{2}$

Resposta: B.

6) Volume da cunha (radianos). Para $r=2\ \text{m}$ e $\theta=\dfrac{\pi}{4}$, o volume da cunha é:

$\dfrac{\pi}{3}\ \text{m}^{3}$
$\dfrac{2\pi}{3}\ \text{m}^{3}$
$\dfrac{4\pi}{3}\ \text{m}^{3}$
$\dfrac{8\pi}{3}\ \text{m}^{3}$

Ver solução

$V_c=\dfrac{2}{3}\theta r^{3}=\dfrac{2}{3}\cdot \dfrac{\pi}{4}\cdot 8=\boxed{\dfrac{4\pi}{3}}\ \text{m}^{3}$

Resposta: C.

7) Custo de pintura. Um globo metálico de raio $0{,}8\ \text{m}$ receberá pintura apenas em um fuso de $\alpha=90^\circ$. O preço é R$ 30,00 por m². O custo aproximado é:

R$ 56,75
R$ 60,32
R$ 63,50
R$ 72,10

Ver solução

$\alpha=90^\circ \Rightarrow A_f=\pi r^{2}=\pi\cdot 0{,}64=2{,}0106\ \text{m}^{2}$

Custo $\approx 2{,}0106\times 30=\boxed{\text{R\$ }60{,}32}$

Resposta: B.

8) Qual fração da esfera? Um fuso ocupa $25\%$ da área da esfera. O ângulo $\alpha$ é:

$60^\circ$
$75^\circ$
$90^\circ$
$120^\circ$

Ver solução

$\alpha/360=0{,}25\Rightarrow \alpha=\boxed{90^\circ}$

Resposta: C.

9) Usando o diâmetro. Uma esfera tem diâmetro $30\ \text{cm}$. Para $\alpha=30^\circ$, a área do fuso (exata) é:

$50\pi\ \text{cm}^{2}$
$60\pi\ \text{cm}^{2}$
$70\pi\ \text{cm}^{2}$
$75\pi\ \text{cm}^{2}$

Ver solução

$r=15\ \text{cm}$

$A_f=\dfrac{\pi\cdot 225\cdot 30}{90}=\dfrac{\pi\cdot 225}{3}=\boxed{75\pi}\ \text{cm}^{2}$

Resposta: D.

10) Encontrando o raio. Um fuso tem $A_f=80\pi\ \text{cm}^{2}$ e $\alpha=120^\circ$. O raio aproximado da esfera é:

$6{,}32\ \text{cm}$
$7{,}35\ \text{cm}$
$7{,}75\ \text{cm}$
$8{,}66\ \text{cm}$

Ver solução

$80\pi=\dfrac{\pi r^{2}\cdot 120}{90}\Rightarrow 80=\dfrac{4}{3}r^{2}$

$r^{2}=60\Rightarrow r=\sqrt{60}= \boxed{7{,}75\ \text{cm}}$

Resposta: C.

11) Volume por proporção. Para $r=6\ \text{cm}$ e $\alpha=45^\circ$, o volume da cunha é:

$24\pi\ \text{cm}^{3}$
$30\pi\ \text{cm}^{3}$
$36\pi\ \text{cm}^{3}$
$48\pi\ \text{cm}^{3}$

Ver solução

$V_c=\dfrac{\pi r^{3}\alpha}{270}=\dfrac{\pi\cdot 216\cdot 45}{270}=\pi\cdot 216\cdot \dfrac{1}{6}=\boxed{36\pi}\ \text{cm}^{3}$

Resposta: C.

12) Determinando o ângulo em radianos. Em uma esfera com $r=5\ \text{cm}$, a área do fuso é $50\pi\ \text{cm}^{2}$. O ângulo $\theta$ (radianos) vale:

$\dfrac{\pi}{2}$
$\dfrac{\pi}{3}$
$\pi$
$\dfrac{2\pi}{3}$

Ver solução

$50\pi=2\theta r^{2}=2\theta\cdot 25 \Rightarrow 50\pi=50\theta\Rightarrow \theta=\boxed{\pi}$

Resposta: C.

13) Soma de fusos. Numa mesma esfera de $r=12\ \text{cm}$, duas faixas não sobrepostas têm $\alpha_1=20^\circ$ e $\alpha_2=35^\circ$. A área total dessas faixas é:

$72\pi\ \text{cm}^{2}$
$88\pi\ \text{cm}^{2}$
$96\pi\ \text{cm}^{2}$
$110\pi\ \text{cm}^{2}$

Ver solução

$A_{\text{total}}=\dfrac{\pi r^{2}(\alpha_1+\alpha_2)}{90}=\dfrac{\pi\cdot 144\cdot 55}{90}$

$A_{\text{total}}=\pi\cdot 144\cdot \dfrac{11}{18}= \boxed{88\pi}\ \text{cm}^{2}$

Resposta: B.

14) Zona horária na Terra. Considere $r\approx 6370\ \text{km}$. O fuso de $\alpha=15^\circ$ (uma hora) tem área aproximada:

$1{,}77\times 10^{7}\ \text{km}^{2}$
$2{,}13\times 10^{7}\ \text{km}^{2}$
$2{,}55\times 10^{7}\ \text{km}^{2}$
$1{,}06\times 10^{7}\ \text{km}^{2}$

Ver solução

$A_f=\dfrac{\pi r^{2}\alpha}{90}=\dfrac{\pi\cdot 6370^{2}\cdot 15}{90}=\dfrac{\pi\cdot 6370^{2}}{6}$

$6370^{2}\approx 40{,}576{,}900\Rightarrow A_f\approx \dfrac{3{,}1416\cdot 40{,}576{,}900}{6}\approx \boxed{2{,}13\times 10^{7}\ \text{km}^{2}}$

Resposta: B.

15) Quantidade de faixas iguais. Um fabricante deseja dividir uma esfera em fusos de mesma largura angular, cada um com $\alpha=12^\circ$. Quantos fusos são necessários para cobrir a esfera inteira, sem sobreposição?

Ver solução

$\text{número}=\dfrac{360^\circ}{\alpha}=\dfrac{360}{12}=\boxed{30}$

Resposta: B.